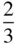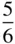We showed in Section 1.4that repetition of an object (e.g. an atom or group of atoms) in a crystal is carried out by operations of rotation, reflection (or inversion) and translation. We have also described in this chapter the consistent combinations of rotations and inversions that can occur in crystals, and in Section 1.8we described the possible translations that can occur in crystals to produce the 14 Bravais lattices, or space lattices.
However, we have so far not made any attempt to combine the operations of rotation (and inversion) with translation, except briefly in Section 1.5, where it was shown that only one‐, two‐, three‐, four‐, and sixfold rotation axes are compatible with translational symmetry. A full description of the symmetry of a crystal involves a description of the way in which all of the symmetry elements are distributed in space. This is called the space group . There are 230 different crystallographic space groups 8; each one gives the fullest description of the symmetry elements present in a crystal possessing that group.
The rotation axes and rotoinversion axes possible in crystals were discussed in Section 2.1and the possible translations in Section 1.8. An enumeration of the way these axes can be consistently combined with the translation is therefore an enumeration of the possible space groups. Space groups are most important in the solution of crystal structures. They are also very useful when establishing symmetry hierarchies in phase transitions in materials such as perovskites [10–12].
When an attempt is made to combine the operations of rotation and translation, the possibility arises naturally of what is called a screw axis . This involves repetition by rotation about an axis, together with translation parallel to that axis. Similarly, a repetition by reflection in a mirror plane may be combined with a translational component parallel to that plane to produce a glide plane . These will now each be considered in more detail.
If, for example, a twofold rotational axis occurs in a crystal, then this means some structural unit or motif is arranged about this direction so that it is repeated by a rotation of 180° about the axis. The repetition shown in Figure 2.22a corresponds to a pure rotational diad axis. However, the rotation of 180° could be coupled with a translation of one‐half of the lattice repeat distance, t , in the direction of the axis to give the screw diad axis shown in Figure 2.22b, denoted by the symbol 2 1. The translation t /2 will be of a length of the order of the lattice parameters of the crystal and hence of the order of a few Ångstrom units (1 Å = 10 −10m), and so quite undetected by the naked eye. Macroscopically, the crystal containing a 2 1axis would then show diad symmetry about that axis in the symmetry of its external faces or of its physical properties.
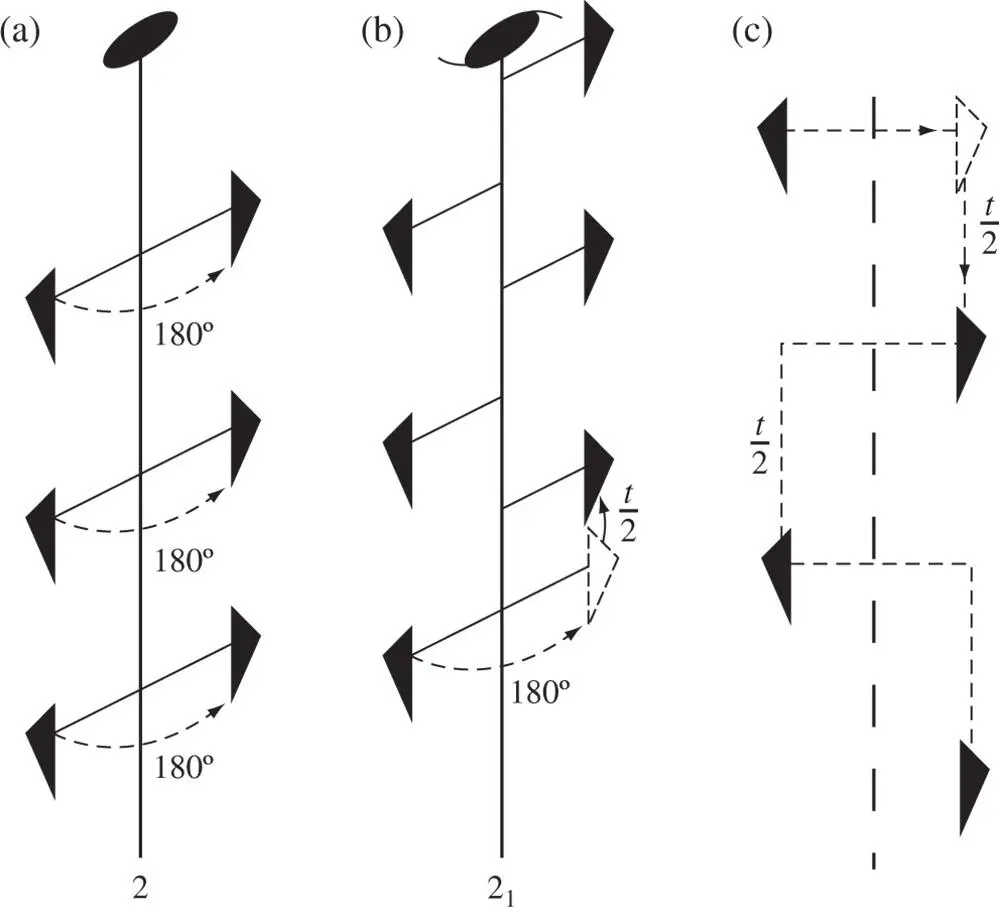
Figure 2.22(a) A twofold rotation axis. (b) A 2 1screw axis. (c) A glide plane normal to the surface of the paper
Although the presence of a screw axis, say a screw diad as in Figure 2.22b, indicates the presence of identical atomic motifs arranged about it so that they are related by a rotation plus translation, the screw axis must not be thought of as translating the translation vectors of the lattice. A screw axis and a pure rotation axis of the same order n repeat a translation in the same way. It follows that the rotational components of screw axes can only be 2 π /1, 2 π /2, 2 π /3, 2 π /4 and 2 π /6, and that an n ‐fold screw and an n ‐fold pure rotation axis must have similar locations with respect to a similar set of translations. The angles between screws and between screws and rotations must therefore be the same as the permissible combinations listed in Table 1.2.
The various kinds of screw axis possible are shown in Table 2.3. An n N‐fold screw axis involves repetition by rotation through 360°/ n with a translation of t N/n , where tis a lattice repeat vector parallel to the axis. There are five types of screw hexad; for example, 6 1involves rotation through 60° and translation of t/6, while 6 5involves rotation through 60° and translation of 5 t/6. By drawing a diagram showing the repetition of objects by these axes, it is easily seen that 6 1is a screw of opposite hand to 6 5, 4 1to 4 3and 6 2to 6 4. A diagram to show this for 3 1and 3 2is given in Figure 2.23. In this figure, A and A′ are lattice points. The operation of 3 1is straightforward, as shown in Figure 2.23a. When repeating an object according to 3 2, note that the object at height 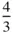 must also occur at height
must also occur at height 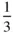 , since A and A′ are both lattice points and the pattern is infinitely long parallel to AA′. It should also be noted that axes 4 2and 6 3include the pure rotation axes 2 and 3 respectively in the lattice. 6 2and 6 4also contain twofold rotation axes.
, since A and A′ are both lattice points and the pattern is infinitely long parallel to AA′. It should also be noted that axes 4 2and 6 3include the pure rotation axes 2 and 3 respectively in the lattice. 6 2and 6 4also contain twofold rotation axes.
Table 2.3Screw axes in crystals
| Name |
Symbol |
Graphical symbol |
Right‐handed screw translation along the axis in units of the lattice parameter |
| Screw diad |
2 1 |
 |
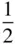 |
| Screw triads |
3 1 |
 |
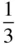 |
|
3 2 |
 |
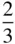 |
| Screw tetrads |
4 1 |
 |
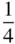 |
|
4 2 |
 |
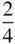 = = 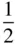 |
|
4 3 |
 |
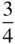 |
| Screw hexads |
6 1 |
 |
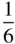 |
|
6 2 |
 |
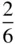 = = 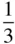 |
|
6 3 |
 |
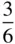 = = 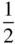 |
|
6 4 |
 |
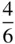 = = 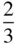 |
|
6 5 |
 |
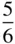 |
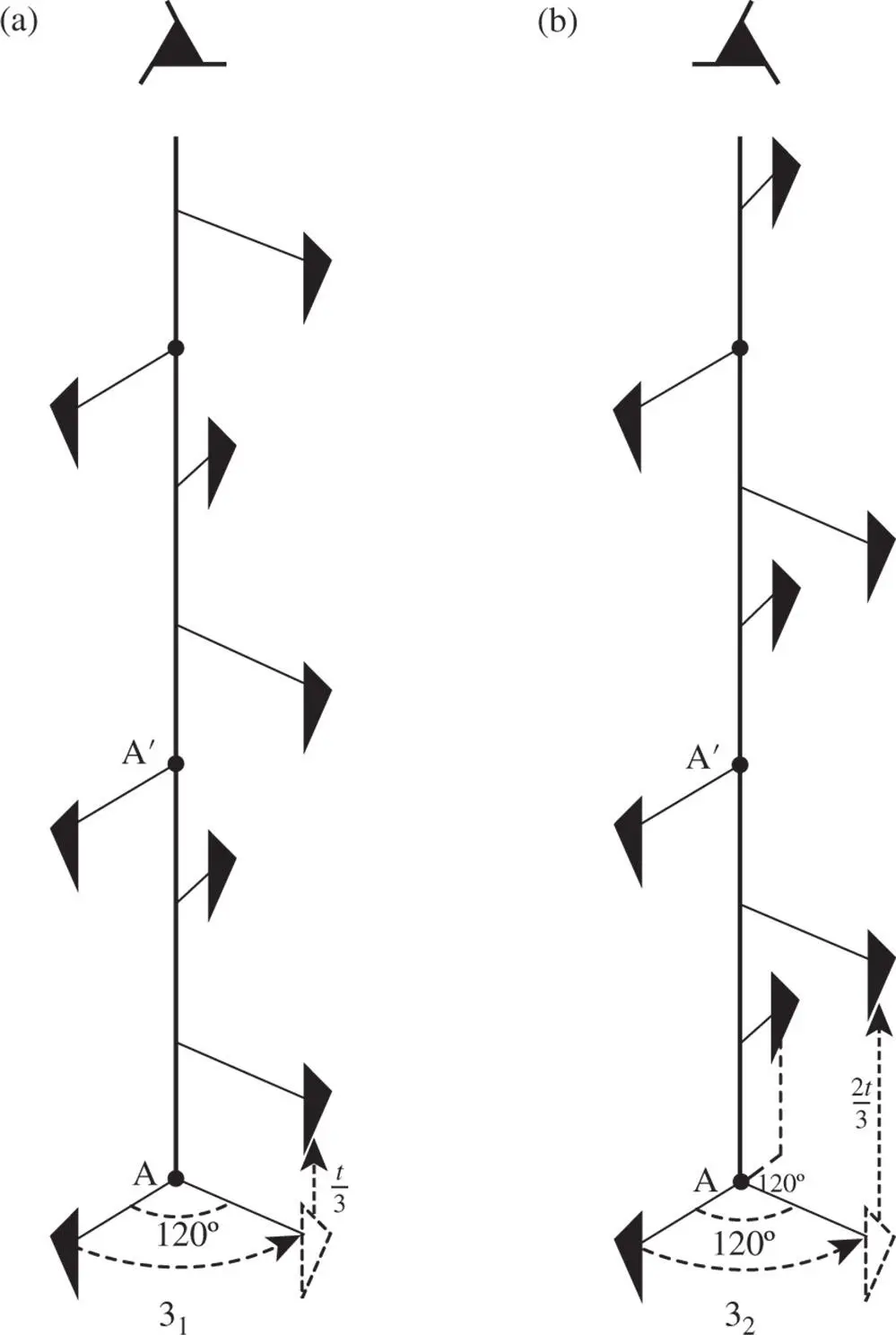
Figure 2.23Screw axes 3 1and 3 2: these are screw axes of opposite hand, as shown by the symbols at the top
Читать дальше


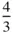 must also occur at height
must also occur at height 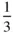 , since A and A′ are both lattice points and the pattern is infinitely long parallel to AA′. It should also be noted that axes 4 2and 6 3include the pure rotation axes 2 and 3 respectively in the lattice. 6 2and 6 4also contain twofold rotation axes.
, since A and A′ are both lattice points and the pattern is infinitely long parallel to AA′. It should also be noted that axes 4 2and 6 3include the pure rotation axes 2 and 3 respectively in the lattice. 6 2and 6 4also contain twofold rotation axes.
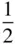

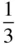

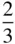

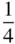

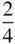 =
= 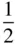

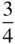

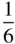

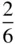 =
= 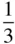

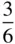 =
= 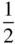

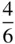 =
=