Anthony Kelly - Crystallography and Crystal Defects
Здесь есть возможность читать онлайн «Anthony Kelly - Crystallography and Crystal Defects» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Crystallography and Crystal Defects
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Crystallography and Crystal Defects: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Crystallography and Crystal Defects»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
explains the modern concepts of crystallography in a clear, succinct manner and shows how to apply these concepts in the analyses of point, line and planar defects in crystalline materials.
Fully revised and updated, this book now includes:
Original source references to key crystallographic terms familiar to materials scientists Expanded discussion on the elasticity of cubic materials New content on texture that contains more detail on Euler angles, orientation distribution functions and an expanded discussion on examples of textures in engineering materials Additional content on dislocations in materials of symmetry lower than cubic An expanded discussion of twinning which includes the description and classification of growth twins The inclusion and explanation of results from atomistic modelling of twin boundaries Problem sets with new questions, detailed worked solutions, supplementary lecture material and online computer programs for crystallographic calculations. Written by authors with extensive lecturing experience at undergraduate level,
continues to take its place as the core text on the topic and provides the essential resource for students and researchers in metallurgy, materials science, physics, chemistry, electrical, civil and mechanical engineering.

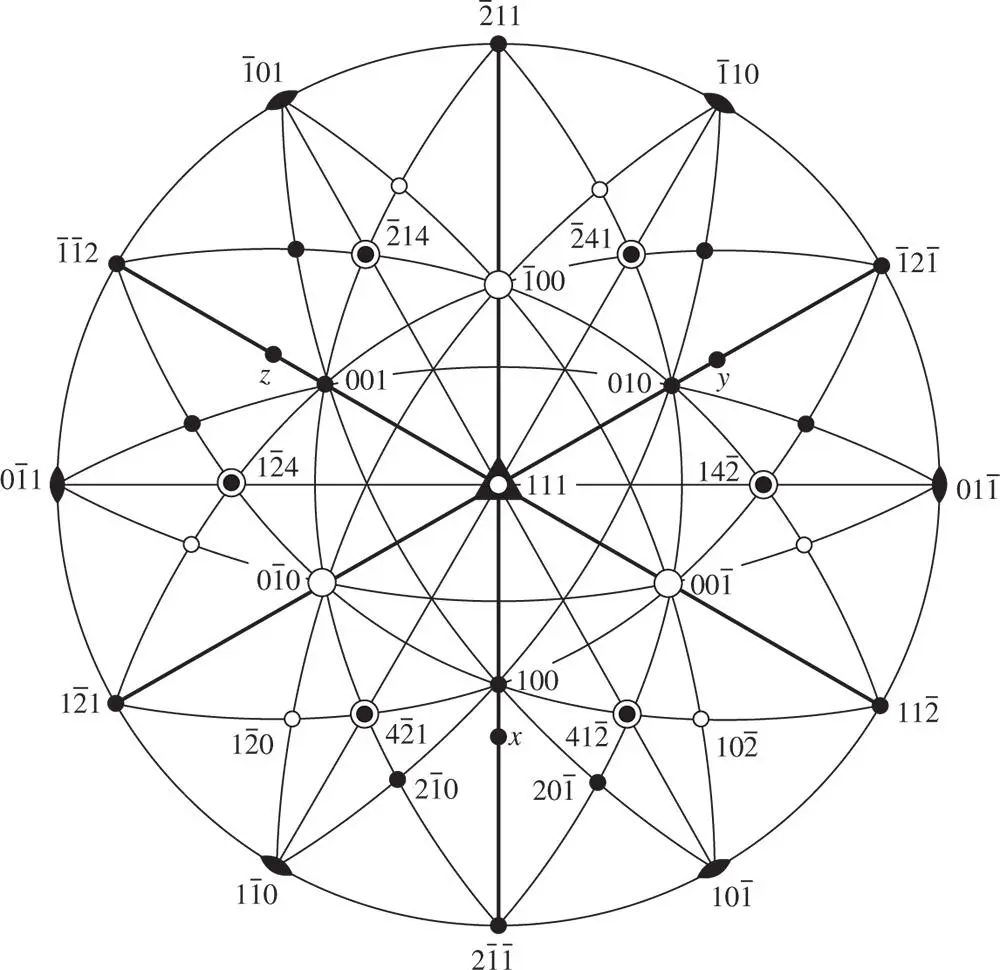
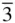 m with a rhombohedral unit cell. When poles in the upper and lower hemispheres coincide in projection, the indices shown refer to the poles in the upper hemisphere
m with a rhombohedral unit cell. When poles in the upper and lower hemispheres coincide in projection, the indices shown refer to the poles in the upper hemisphere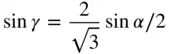
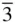 m with planes indexed according to the Miller–Bravais scheme is shown in Figure 2.17. This is the same crystal as that in Figure 2.16( c / a = 1.02). When using the hexagonal cell, the x ‐, y ‐ and u ‐axes are chosen parallel to the diads in
m with planes indexed according to the Miller–Bravais scheme is shown in Figure 2.17. This is the same crystal as that in Figure 2.16( c / a = 1.02). When using the hexagonal cell, the x ‐, y ‐ and u ‐axes are chosen parallel to the diads in 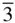 m .
m .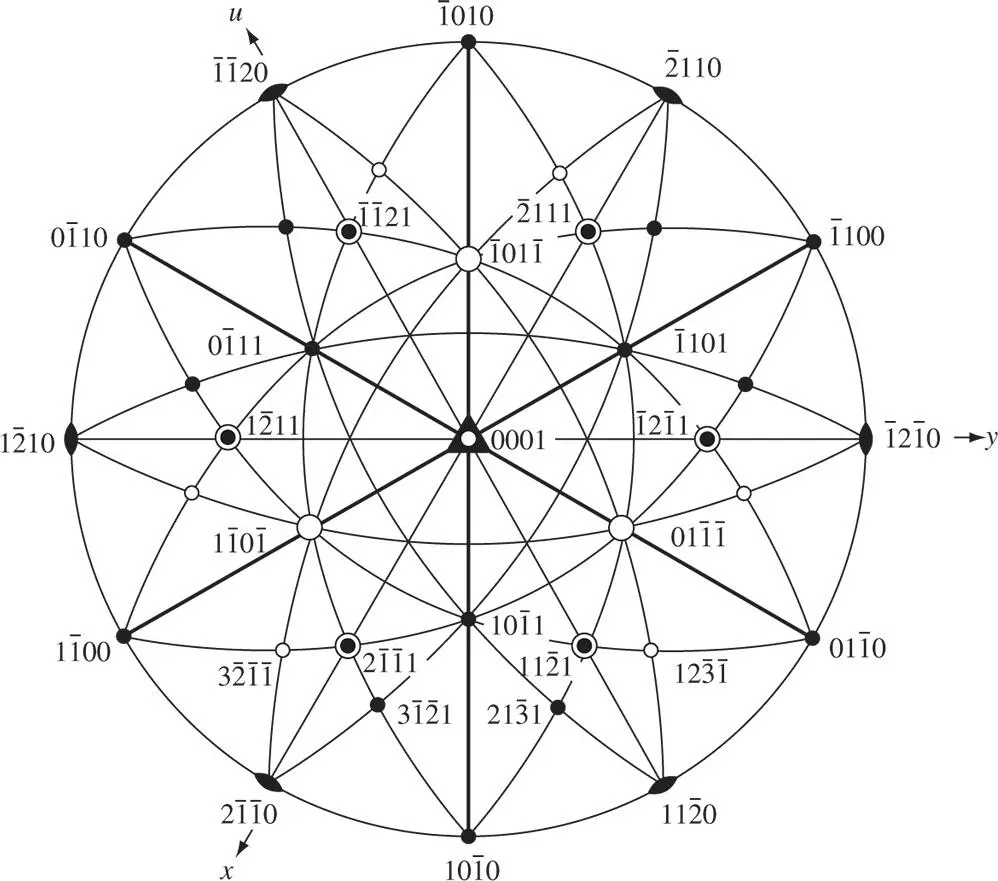
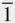 1) || (100). The plane (10
1) || (100). The plane (10  0) in Figure 2.17then has indices (2
0) in Figure 2.17then has indices (2 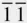 ) in Figure 2.16. The indices (2
) in Figure 2.16. The indices (2 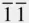 ) could be deduced by noting that the plane (2
) could be deduced by noting that the plane (2 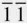 ) contains the [111] direction (and so the pole of (2
) contains the [111] direction (and so the pole of (2 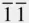 ) must lie on the primitive if [111] is at the centre of the stereogram), is equally inclined to the y ‐ and z ‐axes, and lies in the zone containing (111) and (100). The plotting of a stereogram and the determination of axial ratios for a trigonal crystal referred to hexagonal axes then proceed as for the hexagonal system. 7
) must lie on the primitive if [111] is at the centre of the stereogram), is equally inclined to the y ‐ and z ‐axes, and lies in the zone containing (111) and (100). The plotting of a stereogram and the determination of axial ratios for a trigonal crystal referred to hexagonal axes then proceed as for the hexagonal system. 7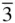 m , special forms lie (i) normal to the triad: {0001}, (ii) parallel to the triad: { hki 0}, (iii) normal to mirror planes: { h 0
m , special forms lie (i) normal to the triad: {0001}, (ii) parallel to the triad: { hki 0}, (iii) normal to mirror planes: { h 0 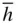 l }, and (iv) equally inclined to two diads { hh
l }, and (iv) equally inclined to two diads { hh 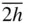 l }. The six faces in the form:{ h 0
l }. The six faces in the form:{ h 0 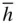 l }, make a rhombohedron; {10
l }, make a rhombohedron; {10 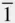 2}would be an example, consisting of the planes (10
2}would be an example, consisting of the planes (10  2), (
2), ( 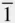 102), (0
102), (0  12), (
12), ( 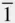 01
01 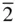 ), (1
), (1 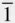 0
0 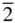 ), and (01
), and (01 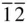 ). This form is similar in appearance to {0 h
). This form is similar in appearance to {0 h 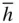 l }, which is also a rhombohedron, rotated 60° with respect to the first one.
l }, which is also a rhombohedron, rotated 60° with respect to the first one.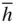 l } and {0 h
l } and {0 h 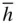 l } (or, equivalently, {0 k
l } (or, equivalently, {0 k 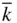 l }) is shown in Figure 2.18. They are actually quite separate forms and each one is a special form. We therefore need to add {0 h
l }) is shown in Figure 2.18. They are actually quite separate forms and each one is a special form. We therefore need to add {0 h 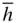 l } to the list of special forms, in addition to { h 0
l } to the list of special forms, in addition to { h 0 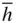 l }. It is apparent from Figure 2.16that when using the rhombohedral cell the two forms {10
l }. It is apparent from Figure 2.16that when using the rhombohedral cell the two forms {10  1} and {01
1} and {01 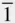 1} have different indices, since the face above (00
1} have different indices, since the face above (00  ) in the projection in Figure 2.16would have indices (22
) in the projection in Figure 2.16would have indices (22 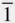 ).
).










