A stereogram of a cubic crystal with the poles of a number of faces indicated, along with the zones in which they lie, is shown in Figure 2.11. Additional poles are easily located on a stereogram, such as that in Figure 2.11, by use of the zone addition rule explained in Section 1.3(Eq. (1.20) and following) and used to plot poles in Section 2.2.
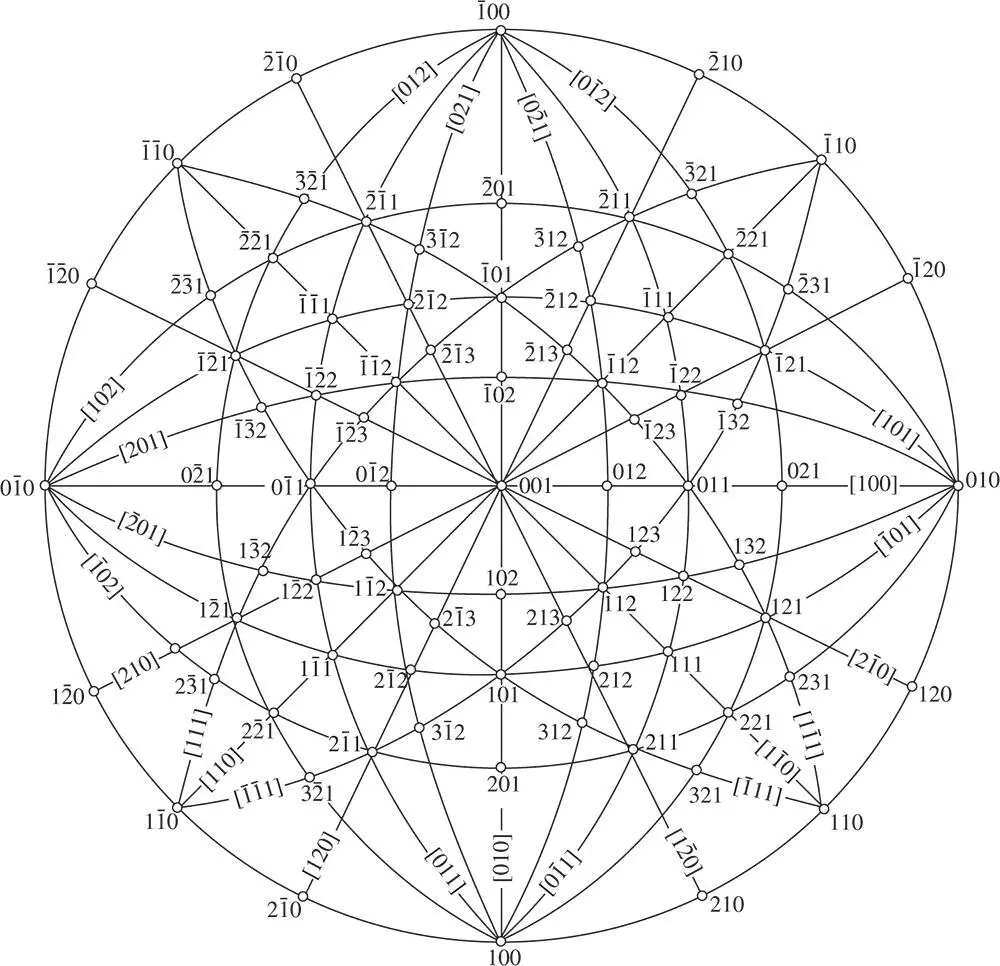
Figure 2.11Stereogram of a cubic crystal.
Source: From [5], p. 82. Copyright 1959.
Crystals possessing a hexad axis have a Bravais lattice, as illustrated in Figure 1.19j in Section 1.8. The x ‐ and y ‐axes are at 120° to one another and perpendicular to the hexagonal axis along z . The holosymmetric class of this system, 6/ mmm , possesses a hexad at the intersection of two sets of three vertical planes of symmetry, two sets of three diad axes normal to these, a plane of symmetry normal to the hexad axis and a centre of symmetry ( Figure 2.6). These symmetry elements are shown in Figure 2.12a. Diad axes at 120° to one another are taken as the crystal axes. If this is done, the indices of a number of faces are as marked in Figure 2.12b. The plane of index (100) is repeated by the hexad axis to give (010), ( 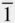 10), (
10), (  00), (0
00), (0 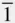 0), (1
0), (1  0). All of these are identical crystallographic planes and yet their Miller indices appear different: note (010) and (
0). All of these are identical crystallographic planes and yet their Miller indices appear different: note (010) and ( 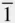 10). To avoid the possibility of confusion from having planes of the same form with quite different indices, it is customary in materials science and metallurgy to employ Miller–Bravais indices for the hexagonal system. 4To do this, we choose a third crystal axis u normal to the hexagonal axis and at 120° to both the x ‐ and the y ‐axes. 5The lattice repeat distance along the u ‐axis is equal to a (= b ) from Figure 1.19j.
10). To avoid the possibility of confusion from having planes of the same form with quite different indices, it is customary in materials science and metallurgy to employ Miller–Bravais indices for the hexagonal system. 4To do this, we choose a third crystal axis u normal to the hexagonal axis and at 120° to both the x ‐ and the y ‐axes. 5The lattice repeat distance along the u ‐axis is equal to a (= b ) from Figure 1.19j.
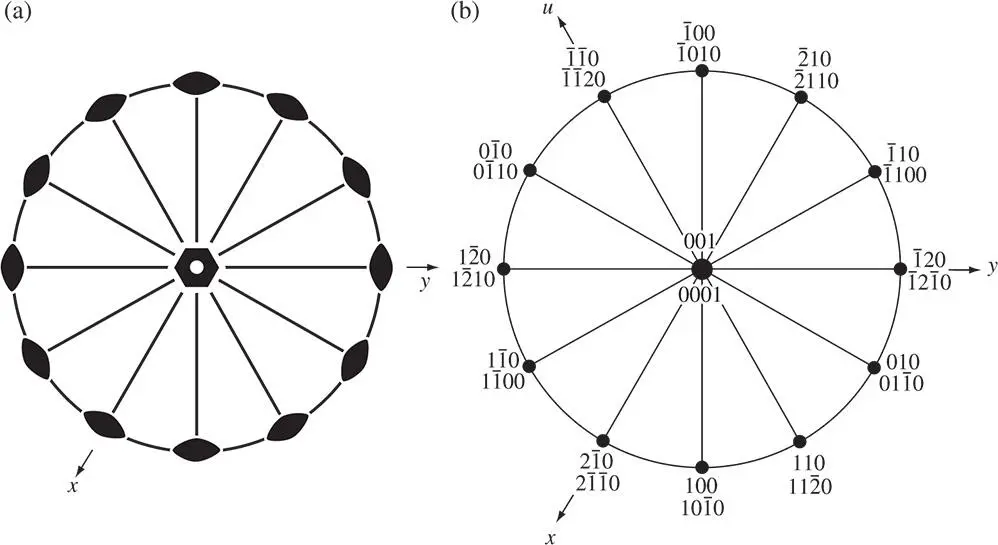
Figure 2.12(a) Stereogram of the holosymmetric class of the hexagonal system, 6/ mmm , (b) indices of a number of poles in both Miller−Bravais and Miller indices on this stereogram
To state the Miller–Bravais indices of a plane we then take the intercepts along all three axes, x , y and u , express these in terms of the lattice parameters and proceed exactly as in Section 1.2. The result is that a plane always has four indices ( hkil ), where i is the intercept along the u ‐axis. It is obvious that there is a necessary relationship between h , k and i since the u ‐axis is a redundant third axis normal to the hexagonal axis. This can be deduced from Figure 2.13and is:
(2.2) 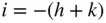
i.e. the third index is always the negative of the sum of the first two. The indices of a number of poles are given in both Miller–Bravais and Miller indices in Figure 2.12b. The hexagonal symmetry is then apparent in the former from the indices of planes of the same form.
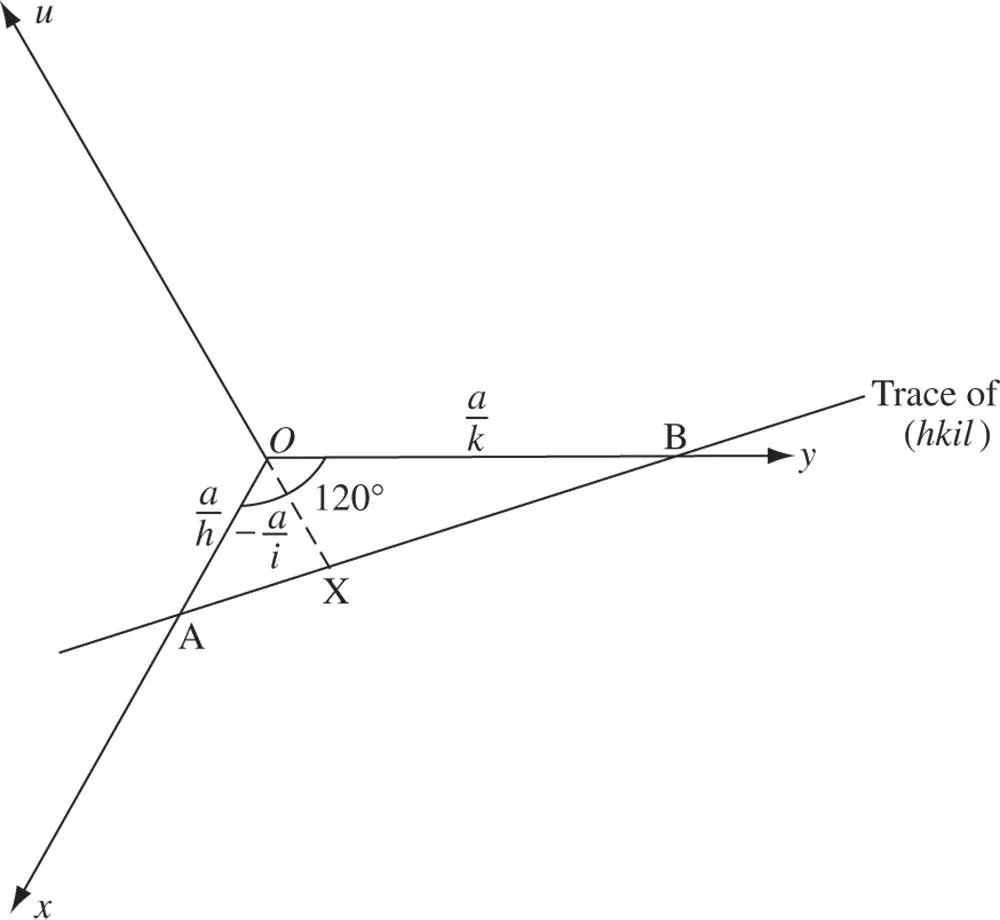
Figure 2.13Geometry to show that in Miller−Bravais indices ( hkil ), i = −( h + k )
A four‐index system due to Leonhard Weber [8] is also used to specify directions in hexagonal crystals so that the index appears as [ UVTW ] instead of [ uvw ]. When this is done, a little care is needed in relating the results to those obtained using a three‐index notation. To enable directions of a given family to have indices of similar appearance, the directions are specified by taking steps along all three axes and arranging it so that the step along the u ‐axis is of such length that the number of unit repeat vectors moved along this direction, T , is equal to the negative of ( U + V ).
In general, the indices [ UVTW ] and [ uvw ] are related to one another through the equations
(2.3) 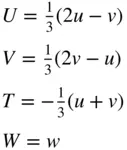
and, conversely,
(2.4) 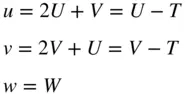
The direction corresponding to the x ‐axis in Figure 2.14is then [2 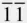 0] in the four‐index notation and [100] in the three‐index system; the magnitude of [2
0] in the four‐index notation and [100] in the three‐index system; the magnitude of [2 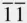 0] is three times that of [100], so therefore [100] in the three‐index system is equivalent in magnitude to the four‐index vector
0] is three times that of [100], so therefore [100] in the three‐index system is equivalent in magnitude to the four‐index vector 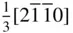 . Likewise, [010] in the three‐index system is equivalent in magnitude to the four‐index vector
. Likewise, [010] in the three‐index system is equivalent in magnitude to the four‐index vector 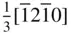 and
and 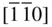 to
to 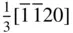 . Knowing the four‐index vectors equivalent in magnitude and direction to the three‐index vectors [100] and [010] enables more general three‐index vectors [ uvw ] to be transformed into their four‐index equivalent vectors relatively easily prior to the clearing of fractions to specify four‐index zones or directions.
. Knowing the four‐index vectors equivalent in magnitude and direction to the three‐index vectors [100] and [010] enables more general three‐index vectors [ uvw ] to be transformed into their four‐index equivalent vectors relatively easily prior to the clearing of fractions to specify four‐index zones or directions.
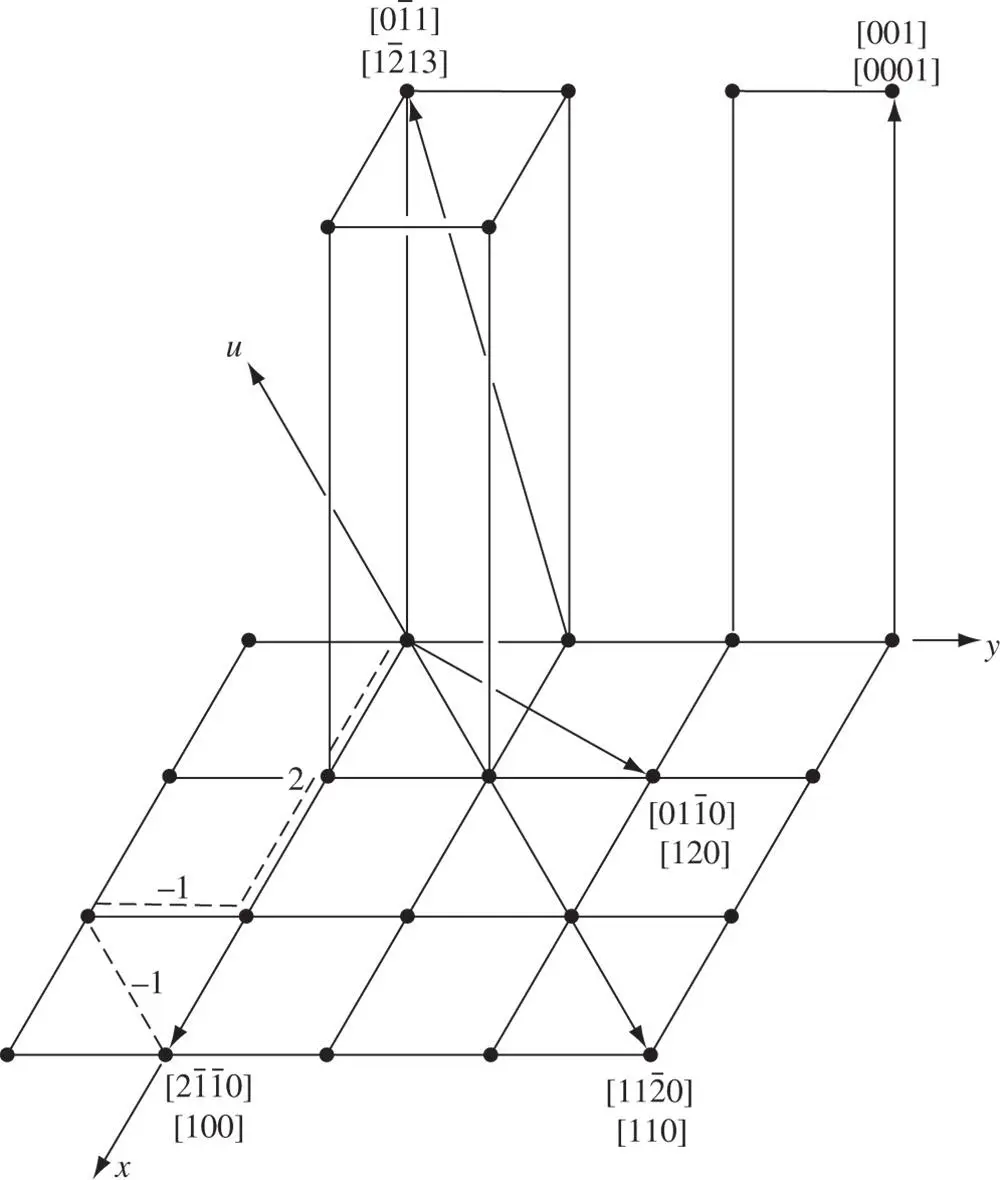
Figure 2.14Indices of various directions in the hexagonal system specified in both the conventional three‐index notation, [ uvw ], and the four‐index Weber notation, [ UVTW ]
Some indices of directions specified in both ways are given in Figure 2.14. In relating planes and zone axes using Eq. (1.6), it is usually best to work entirely in the three‐index notation for both planes and directions and to translate the three‐index notation for a direction into the four‐index system at the end of the calculation. It is also useful to note that the condition needed for a four‐index vector [ UVTW ] to lie in a four‐index plane ( hkil ) is:
Читать дальше


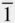 10), (
10), (  00), (0
00), (0 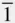 0), (1
0), (1  0). All of these are identical crystallographic planes and yet their Miller indices appear different: note (010) and (
0). All of these are identical crystallographic planes and yet their Miller indices appear different: note (010) and ( 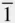 10). To avoid the possibility of confusion from having planes of the same form with quite different indices, it is customary in materials science and metallurgy to employ Miller–Bravais indices for the hexagonal system. 4To do this, we choose a third crystal axis u normal to the hexagonal axis and at 120° to both the x ‐ and the y ‐axes. 5The lattice repeat distance along the u ‐axis is equal to a (= b ) from Figure 1.19j.
10). To avoid the possibility of confusion from having planes of the same form with quite different indices, it is customary in materials science and metallurgy to employ Miller–Bravais indices for the hexagonal system. 4To do this, we choose a third crystal axis u normal to the hexagonal axis and at 120° to both the x ‐ and the y ‐axes. 5The lattice repeat distance along the u ‐axis is equal to a (= b ) from Figure 1.19j.
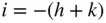

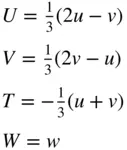
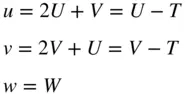
 0] in the four‐index notation and [100] in the three‐index system; the magnitude of [2
0] in the four‐index notation and [100] in the three‐index system; the magnitude of [2  0] is three times that of [100], so therefore [100] in the three‐index system is equivalent in magnitude to the four‐index vector
0] is three times that of [100], so therefore [100] in the three‐index system is equivalent in magnitude to the four‐index vector 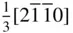 . Likewise, [010] in the three‐index system is equivalent in magnitude to the four‐index vector
. Likewise, [010] in the three‐index system is equivalent in magnitude to the four‐index vector 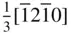 and
and 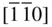 to
to 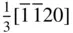 . Knowing the four‐index vectors equivalent in magnitude and direction to the three‐index vectors [100] and [010] enables more general three‐index vectors [ uvw ] to be transformed into their four‐index equivalent vectors relatively easily prior to the clearing of fractions to specify four‐index zones or directions.
. Knowing the four‐index vectors equivalent in magnitude and direction to the three‐index vectors [100] and [010] enables more general three‐index vectors [ uvw ] to be transformed into their four‐index equivalent vectors relatively easily prior to the clearing of fractions to specify four‐index zones or directions.











