A crystal in this system contains three diads, which must be at right angles to one another. In Figure 2.6they are the crystal axes. From Table 1.3 and Figures 1.19d, e, f and g, the lattice parameters may be all unequal.
The point group containing just three diad axes at right angles to one another is shown in Figure 2.6and is designated 222. In general, a pole in a crystal belonging to this point group is repeated four times. If the indices of the initial pole are ( hkl ), where there is no special relationship between h, k and l , the operation of all of the symmetry elements of the point group on this one initial pole produces three other poles. These are 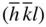 ,
, 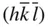 and
and 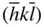 ( Figure 2.7). The assemblage of crystal faces produced by repetition of an initial crystal face with indices ( hkl ) is called the form hkl and is given the symbol { hkl }. 3If the assemblage of faces encloses space, the form is said to be closed; otherwise it is open. In this case, { hkl } is closed. The symbol { hkl } with curly brackets means all faces of the form hkl . Here, for the point group 222, this means ( hkl ),
( Figure 2.7). The assemblage of crystal faces produced by repetition of an initial crystal face with indices ( hkl ) is called the form hkl and is given the symbol { hkl }. 3If the assemblage of faces encloses space, the form is said to be closed; otherwise it is open. In this case, { hkl } is closed. The symbol { hkl } with curly brackets means all faces of the form hkl . Here, for the point group 222, this means ( hkl ),  ,
, 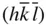 and
and 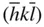 . The form { hkl } is said to show a multiplicity of four. Then { hkl } would be said to be a general form ; that is, a form that bears no special relationship to the symmetry elements of the point group.
. The form { hkl } is said to show a multiplicity of four. Then { hkl } would be said to be a general form ; that is, a form that bears no special relationship to the symmetry elements of the point group.
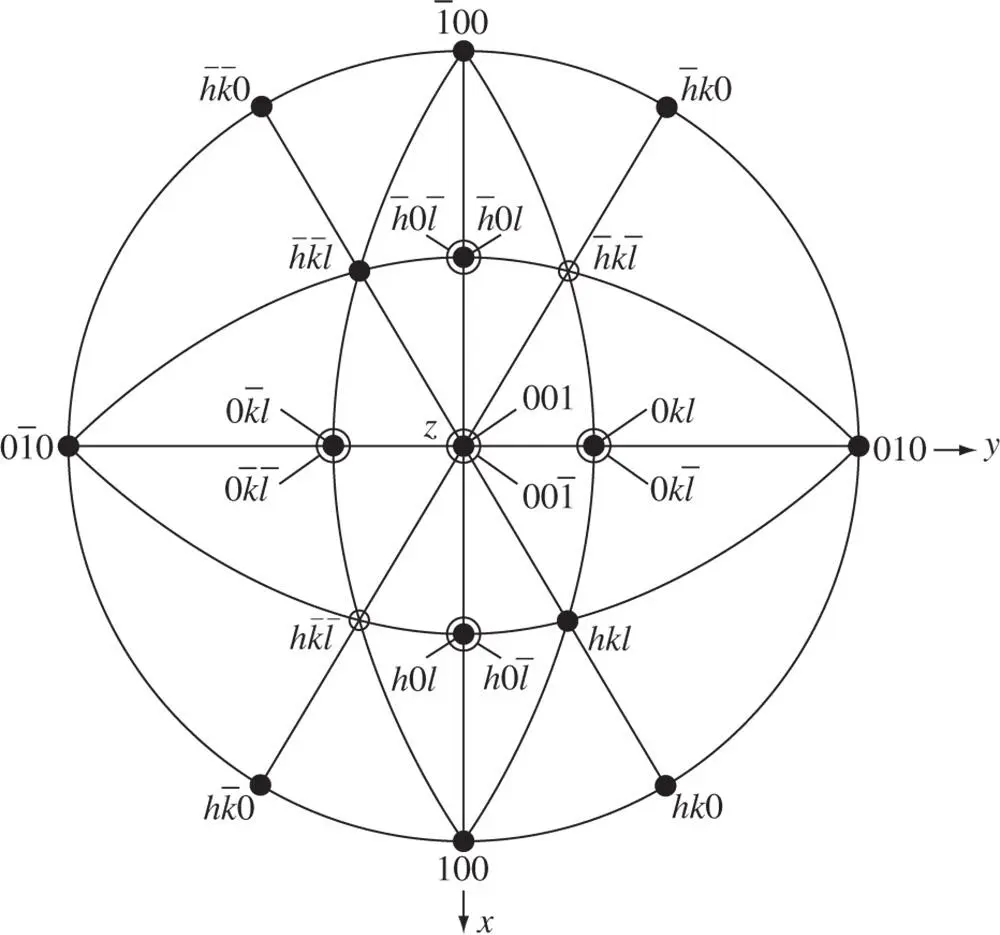
Figure 2.7A stereogram of an orthorhombic crystal of point group 222 centred on 001. The diad axes are parallel to the x ‐, y ‐ and z ‐axes
Special forms in this crystal class would be {100}, {010} and {001}; each of these forms gives just two faces: for {100}, these would be the faces (100) and ( 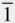 00) ( Figure 2.7). These forms are all open ones. They are easily recognized as special forms since their multiplicity is less than that of the general form. Forms such as { hk 0}, { h 0 l } and {0 kl } which have one index zero and no special relationship between the other two would also be described as special, even though, as is evident from Figure 2.7, the multiplicity of each is four, as for the general form in this crystal class. One reason for this is that these poles lie normal to a diad axis. This is a special position with respect to this axis and has the result that if a crystal grew with faces parallel only to the planes of indices { hk 0}, { h 0 l } and {0 kl }, it would appear to show mirror symmetry as well as the three diad axes. A second reason is that each of the { hk 0}, { h 0 l } and {0 kl } forms is open, while the general { hkl } form is closed. Special forms usually correspond to poles lying normal to or on an axis of symmetry, and normal to or on mirror planes, and sometimes to poles lying midway between two axes of symmetry. However, the best definition of a special form is as follows: a form is special if the development of the complete form shows a symmetry of arrangement of the poles which is higher than the one the crystal actually possesses. Special forms in all of the crystal classes are listed later, in Table 2.1.
00) ( Figure 2.7). These forms are all open ones. They are easily recognized as special forms since their multiplicity is less than that of the general form. Forms such as { hk 0}, { h 0 l } and {0 kl } which have one index zero and no special relationship between the other two would also be described as special, even though, as is evident from Figure 2.7, the multiplicity of each is four, as for the general form in this crystal class. One reason for this is that these poles lie normal to a diad axis. This is a special position with respect to this axis and has the result that if a crystal grew with faces parallel only to the planes of indices { hk 0}, { h 0 l } and {0 kl }, it would appear to show mirror symmetry as well as the three diad axes. A second reason is that each of the { hk 0}, { h 0 l } and {0 kl } forms is open, while the general { hkl } form is closed. Special forms usually correspond to poles lying normal to or on an axis of symmetry, and normal to or on mirror planes, and sometimes to poles lying midway between two axes of symmetry. However, the best definition of a special form is as follows: a form is special if the development of the complete form shows a symmetry of arrangement of the poles which is higher than the one the crystal actually possesses. Special forms in all of the crystal classes are listed later, in Table 2.1.
Table 2.1Special forms in the crystal classes
| 2 |
32 |
6 mm |
{010}, {0  0}, { h 0 l } 0}, { h 0 l } |
{0001}, 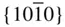 , , 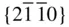 , , 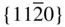 , { hki 0}, , { hki 0}, 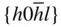 , , 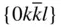 , , 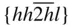 , , 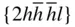 |
{0001}, 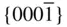 , , 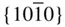 , , 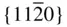 , { hki 0}, , { hki 0}, 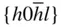 , , 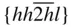 |
| m and 2/ m |
4 |
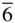 m 2 m 2 |
| {010}, { h 0 l } |
{001}, 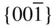 , { hk 0} , { hk 0} |
{0001}, 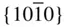 , , 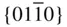 , , 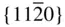 , { hki 0}, , { hki 0}, 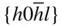 , , 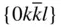 , , 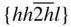 |
| mm 2 |
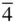 and 4/ m and 4/ m |
622 and 6/ mmm |
{001}, 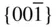 , {100}, {010}, { hk 0}, { h 0 l }, {0 kl } , {100}, {010}, { hk 0}, { h 0 l }, {0 kl } |
{001}, { hk 0} |
{0001}, 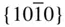 , , 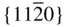 , { hki 0}, , { hki 0}, 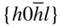 , , 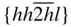 |
| 222 and mmm |
4 mm |
23 |
| {100}, {010}, {001}, { hk 0}, { h 0 l }, {0 kl } |
{001}, 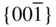 , {100}, {110}, { hk 0}, { h 0 l }, { hhl } , {100}, {110}, { hk 0}, { h 0 l }, { hhl } |
{100}, {110}, { hk 0}, { kh 0}, {111}, {1  1}, { hll }, 1}, { hll }, 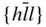 , { hhl }, , { hhl }, 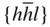 |
| 3 |
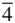 2 m 2 m |
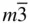 |
{0001}, 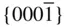 , { hki 0} , { hki 0} |
{001}, {100}, {110}, { hk 0}, { h 0 l }, { hhl }, 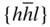 |
{100}, {110}, { hk 0}, { kh 0}, {111}, { hll }, { hhl } |
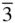 |
42 and 4/ mmm |
432 |
| {0001}, { hki 0} |
{001}, {100}, {110}, { hk 0}, { h 0 l }, { hhl } |
{100}, {110}, { hk 0}, {111}, { hll }, { hhl } |
| 3 m |
6 |
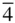 3 m 3 m |
{0001}, 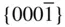 , , 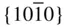 , , 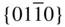 , , 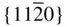 , { hki 0}, , { hki 0}, 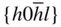 , , 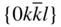 , , 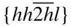 |
{0001}, 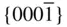 , { hki 0} , { hki 0} |
{100}, {110}, { hk 0}, {111}, {1 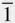 1}, { hll }, { h 1}, { hll }, { h 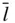 l }, { hhl }, l }, { hhl }, 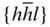 |
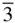 m m |
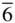 and 6/ m and 6/ m |
m 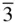 m m |
{0001}, 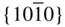 , , 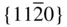 , { hki 0}, , { hki 0}, 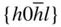 , , 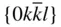 , , 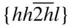 |
{0001}, { hki 0} |
{100}, {110}, { hk 0}, {111}, { hll }, { hhl } |
The orthorhombic system also contains the classes 2 mm and mmm ( Figure 2.6). The former contains two mirror planes, which must be at right angles. Two mirror planes at right angles automatically show diad symmetry along the line of intersection ( Figure 2.6). Since m ≡ 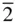 , this group could be designated 2
, this group could be designated 2 
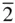 , and this is why it appears in the orthorhombic system, which is defined as possessing three diad axes. This crystal class could simply be designated mm since the diad is automatically present. However, mm 2 is usually used for the later development of space groups (see Section 2.12). A crystal containing three diad axes can also contain mirrors normal to all of these without an axis of higher symmetry. Such a point group is designated mmm , or could be designated 2/ mm . As can be seen from Figure 2.6, the multiplicity of the general form is now eight. The special forms { hk 0}, { h 0 l } and {0 kl } now show a lower multiplicity than the general one. The point group mmm shows the highest symmetry in the orthorhombic system. The point group showing the highest symmetry in a particular crystal system is said to be the holosymmetric class.
, and this is why it appears in the orthorhombic system, which is defined as possessing three diad axes. This crystal class could simply be designated mm since the diad is automatically present. However, mm 2 is usually used for the later development of space groups (see Section 2.12). A crystal containing three diad axes can also contain mirrors normal to all of these without an axis of higher symmetry. Such a point group is designated mmm , or could be designated 2/ mm . As can be seen from Figure 2.6, the multiplicity of the general form is now eight. The special forms { hk 0}, { h 0 l } and {0 kl } now show a lower multiplicity than the general one. The point group mmm shows the highest symmetry in the orthorhombic system. The point group showing the highest symmetry in a particular crystal system is said to be the holosymmetric class.
Читать дальше

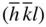 ,
, 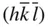 and
and 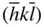 ( Figure 2.7). The assemblage of crystal faces produced by repetition of an initial crystal face with indices ( hkl ) is called the form hkl and is given the symbol { hkl }. 3If the assemblage of faces encloses space, the form is said to be closed; otherwise it is open. In this case, { hkl } is closed. The symbol { hkl } with curly brackets means all faces of the form hkl . Here, for the point group 222, this means ( hkl ),
( Figure 2.7). The assemblage of crystal faces produced by repetition of an initial crystal face with indices ( hkl ) is called the form hkl and is given the symbol { hkl }. 3If the assemblage of faces encloses space, the form is said to be closed; otherwise it is open. In this case, { hkl } is closed. The symbol { hkl } with curly brackets means all faces of the form hkl . Here, for the point group 222, this means ( hkl ),  ,
, 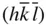 and
and 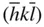 . The form { hkl } is said to show a multiplicity of four. Then { hkl } would be said to be a general form ; that is, a form that bears no special relationship to the symmetry elements of the point group.
. The form { hkl } is said to show a multiplicity of four. Then { hkl } would be said to be a general form ; that is, a form that bears no special relationship to the symmetry elements of the point group.
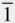 00) ( Figure 2.7). These forms are all open ones. They are easily recognized as special forms since their multiplicity is less than that of the general form. Forms such as { hk 0}, { h 0 l } and {0 kl } which have one index zero and no special relationship between the other two would also be described as special, even though, as is evident from Figure 2.7, the multiplicity of each is four, as for the general form in this crystal class. One reason for this is that these poles lie normal to a diad axis. This is a special position with respect to this axis and has the result that if a crystal grew with faces parallel only to the planes of indices { hk 0}, { h 0 l } and {0 kl }, it would appear to show mirror symmetry as well as the three diad axes. A second reason is that each of the { hk 0}, { h 0 l } and {0 kl } forms is open, while the general { hkl } form is closed. Special forms usually correspond to poles lying normal to or on an axis of symmetry, and normal to or on mirror planes, and sometimes to poles lying midway between two axes of symmetry. However, the best definition of a special form is as follows: a form is special if the development of the complete form shows a symmetry of arrangement of the poles which is higher than the one the crystal actually possesses. Special forms in all of the crystal classes are listed later, in Table 2.1.
00) ( Figure 2.7). These forms are all open ones. They are easily recognized as special forms since their multiplicity is less than that of the general form. Forms such as { hk 0}, { h 0 l } and {0 kl } which have one index zero and no special relationship between the other two would also be described as special, even though, as is evident from Figure 2.7, the multiplicity of each is four, as for the general form in this crystal class. One reason for this is that these poles lie normal to a diad axis. This is a special position with respect to this axis and has the result that if a crystal grew with faces parallel only to the planes of indices { hk 0}, { h 0 l } and {0 kl }, it would appear to show mirror symmetry as well as the three diad axes. A second reason is that each of the { hk 0}, { h 0 l } and {0 kl } forms is open, while the general { hkl } form is closed. Special forms usually correspond to poles lying normal to or on an axis of symmetry, and normal to or on mirror planes, and sometimes to poles lying midway between two axes of symmetry. However, the best definition of a special form is as follows: a form is special if the development of the complete form shows a symmetry of arrangement of the poles which is higher than the one the crystal actually possesses. Special forms in all of the crystal classes are listed later, in Table 2.1. 0}, { h 0 l }
0}, { h 0 l }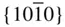 ,
, 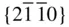 ,
, 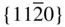 , { hki 0},
, { hki 0}, 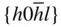 ,
, 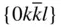 ,
, 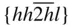 ,
, 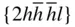
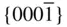 ,
, 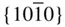 ,
, 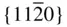 , { hki 0},
, { hki 0}, 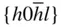 ,
, 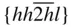
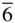 m 2
m 2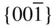 , { hk 0}
, { hk 0}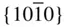 ,
, 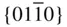 ,
, 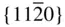 , { hki 0},
, { hki 0}, 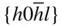 ,
, 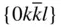 ,
, 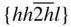
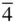 and 4/ m
and 4/ m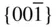 , {100}, {010}, { hk 0}, { h 0 l }, {0 kl }
, {100}, {010}, { hk 0}, { h 0 l }, {0 kl }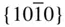 ,
, 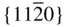 , { hki 0},
, { hki 0}, 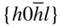 ,
, 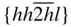
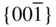 , {100}, {110}, { hk 0}, { h 0 l }, { hhl }
, {100}, {110}, { hk 0}, { h 0 l }, { hhl } 1}, { hll },
1}, { hll }, 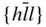 , { hhl },
, { hhl }, 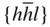
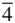 2 m
2 m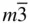
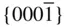 , { hki 0}
, { hki 0}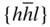
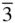
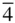 3 m
3 m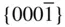 ,
, 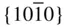 ,
, 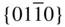 ,
, 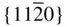 , { hki 0},
, { hki 0}, 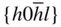 ,
, 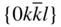 ,
, 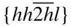
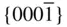 , { hki 0}
, { hki 0}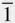 1}, { hll }, { h
1}, { hll }, { h 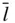 l }, { hhl },
l }, { hhl }, 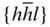
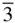 m
m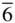 and 6/ m
and 6/ m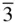 m
m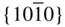 ,
, 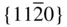 , { hki 0},
, { hki 0}, 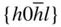 ,
, 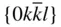 ,
, 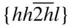
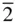 , this group could be designated 2
, this group could be designated 2 
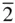 , and this is why it appears in the orthorhombic system, which is defined as possessing three diad axes. This crystal class could simply be designated mm since the diad is automatically present. However, mm 2 is usually used for the later development of space groups (see Section 2.12). A crystal containing three diad axes can also contain mirrors normal to all of these without an axis of higher symmetry. Such a point group is designated mmm , or could be designated 2/ mm . As can be seen from Figure 2.6, the multiplicity of the general form is now eight. The special forms { hk 0}, { h 0 l } and {0 kl } now show a lower multiplicity than the general one. The point group mmm shows the highest symmetry in the orthorhombic system. The point group showing the highest symmetry in a particular crystal system is said to be the holosymmetric class.
, and this is why it appears in the orthorhombic system, which is defined as possessing three diad axes. This crystal class could simply be designated mm since the diad is automatically present. However, mm 2 is usually used for the later development of space groups (see Section 2.12). A crystal containing three diad axes can also contain mirrors normal to all of these without an axis of higher symmetry. Such a point group is designated mmm , or could be designated 2/ mm . As can be seen from Figure 2.6, the multiplicity of the general form is now eight. The special forms { hk 0}, { h 0 l } and {0 kl } now show a lower multiplicity than the general one. The point group mmm shows the highest symmetry in the orthorhombic system. The point group showing the highest symmetry in a particular crystal system is said to be the holosymmetric class.










