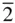Anthony Kelly - Crystallography and Crystal Defects

10 10 Depending on how the motif showing fourfold symmetry is arranged with respect to the two axes of the crystal – the sides of the square in Figure 1.14b – additional symmetry elements may arise. A full discussion of this point for any of the arrangements of symmetry elements in Figure 1.14– that is, a discussion of consistent arrangements of symmetry elements in space – would take us immediately into the subject of space groups. We defer this until much later (see Section 2.12), but the discerning reader may wish to glance at Section 2.12before proceeding further, both to gain reassurance that this subject matter is understood and to appreciate the mass of detail which is avoided by not following up this question now. The question of how additional symmetry elements may arise is considered in Problem 1.14.

11 11 This conforms to the notation used by Buerger [7].

12 12 These are termed Bravais lattices after Auguste Bravais (1811–1863). Eight years before Bravais wrote about the space filling of lattices, Moritz Ludwig Frankenheim (1801–1869) published his book System der Krystalle in which he also considered the same problem [13]. Frankenheim believed he had identified 15 arrangements. However, two of these in the monoclinic system (C and I) were shown by Bravais in a footnote on page 97 of his 1850 article to be equivalent [14]. This equivalence is shown in Figure 1.22. As a consequence of Bravais showing that the monoclinic C and I lattices are identical, these space lattices are known as Bravais lattices, rather than Frankenheim lattices.

13 13 The validity of this statement does not follow immediately at this point. Its truth is plausible if it is noted, as shown later ( Section 2.1), that an inverse diad axis plus a centre of symmetry is equivalent to a diad axis normal to a mirror plane, and that the lattice points of a lattice are centres of symmetry of the lattice.

14 14 A means a lattice point on the (100) face, B a lattice point on (010), and C a lattice point on (001), in all crystal systems.

The macroscopically measured properties of a crystal, such as electrical resistance, thermal expansion, optical properties, magnetic susceptibility and the elastic constants, show a symmetry which can be defined and understood without reference to the translational symmetry elements defined by the lattice. If the translational symmetry of the crystal is disregarded, the remaining symmetry elements (such as axes of rotational symmetry, mirror planes and any centre of inversion), themselves consistent with the translational symmetry of the lattice, can be arranged into 32 consistent groups. These are the 32 crystallographic point groups. They are so called because they are consistent with translational symmetry and because all of the symmetry elements in a group pass through a single point and the operation of these elements leaves just one point unmoved – the point through which they pass. Other point groups, such as the point group symmetry of the icosahedron, which we shall consider in Chapter 4 when discussing the point group symmetries exhibited by quasicrystals, are not compatible with translational symmetry.

The axes of rotational symmetry, the mirror plane and the centre of inversion are all called macroscopic symmetry elements because their presence or absence in a given crystal can be decided in principle by macroscopic tests, such as etching of the crystal, the arrangement of the external faces or the symmetry of the physical properties, without any reference to the atomic structure of the crystal. The macroscopic symmetry elements are of two kinds. A symmetry operation of the first kind , such as a pure rotation axis, when operating on a right‐handed object (say) produces a right‐handed object from it, and all subsequent repetitions of this object are also right‐handed. A symmetry operation of the second kind repeats an enantiomorphous object from an original object. The left and right hands of the ideal external form of the human body are enantiomorphously related. The operation of reflection illustrated in Figure 1.12is an example of a symmetry operation of the second kind since a left‐handed object is repeated from an original right‐handed object. Subsequent operation of the same symmetry element would produce a right‐handed object again and then a left‐handed object, and so forth. A symmetry operation of the second kind therefore involves a reversal of sense in the operation of repetition. Inversion through a centre is also an operation of the second kind.

In developing the 32 crystallographic point groups it is convenient to have all the macroscopic symmetry elements represented by axes and to do this we define what are called improper rotations . These produce repetition by a combination of a rotation and an operation of inversion. We shall use rotoinversion axes. These involve rotation coupled with inversion through a centre. 1A pure rotation axis is said to produce a proper rotation.

The basic operation of repetition by a rotation axis is shown schematically in Figure 2.1. An n ‐fold axis repeats an object by successive rotations through an angle of 2 π / n . In the example shown in Figure 2.1, the axis is one of fourfold symmetry. The operations of monad, diad, triad, tetrad, and hexad pure rotation axes on a single initial pole are shown in Figure 2.2. These diagrams are stereograms (see Appendix 2) with the pole of the axis at the centre of the primitive circle. Dots are used to represent poles in the northern hemisphere of projection related to one another by the rotation axis. The numbers below the stereograms give the shorthand labels for the axes 1, 2, 3, 4 and 6, indicating a onefold, twofold, threefold, fourfold, and sixfold axis, respectively. The repetition of an object by a mirror plane, symbol m , and by a centre of symmetry (or centre of inversion) is shown in Figure 2.3. In Figure 2.3a the mirror plane lies normal to the primitive circle. It is denoted by a strong vertical line | coinciding with the mirror in the stereographic projection. In Figure 2.3b the mirror coincides with the primitive; the dot representing the pole in the northern hemisphere has as its mirror image the circle shown in the southern hemisphere. In Figure 2.3c the centre of inversion is at the centre of the sphere of projection.

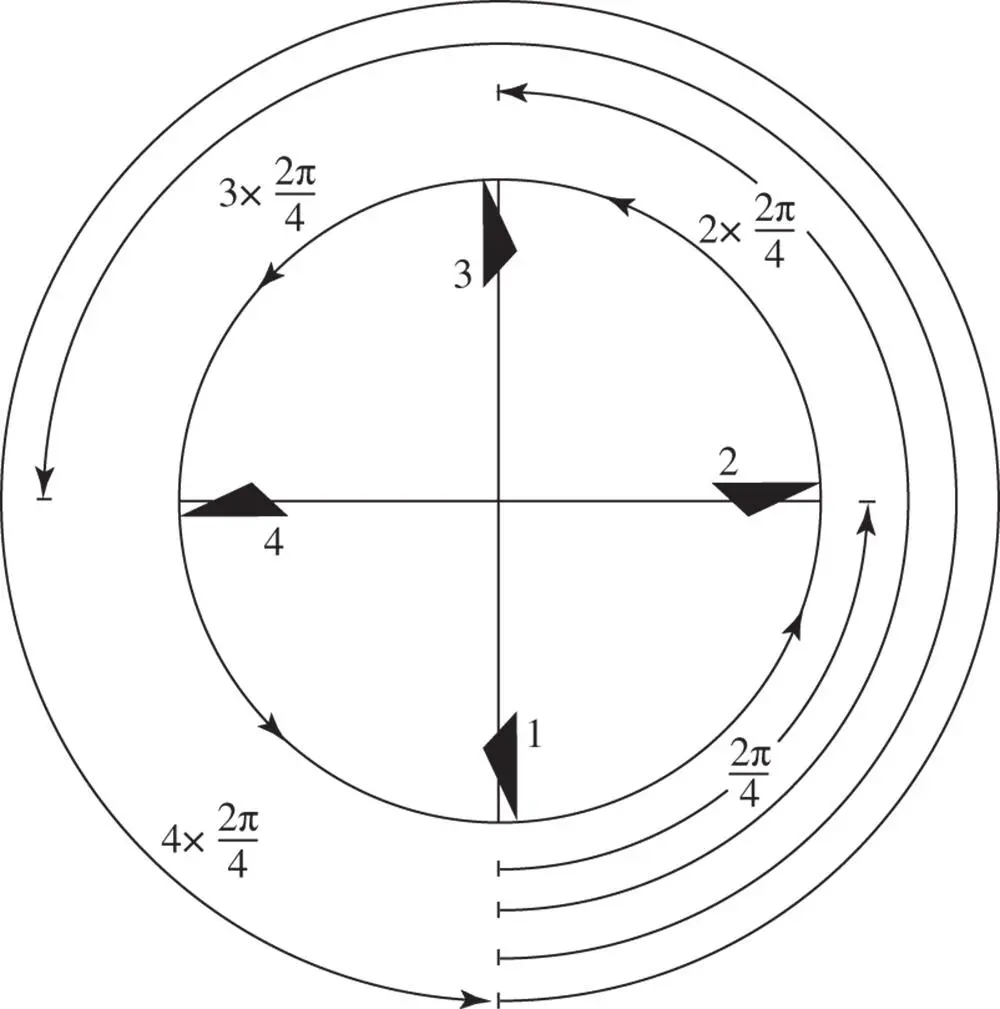
Figure 2.1The basic operation of repetition by a rotation axis. In this example, the axis is a four‐fold symmetry axis

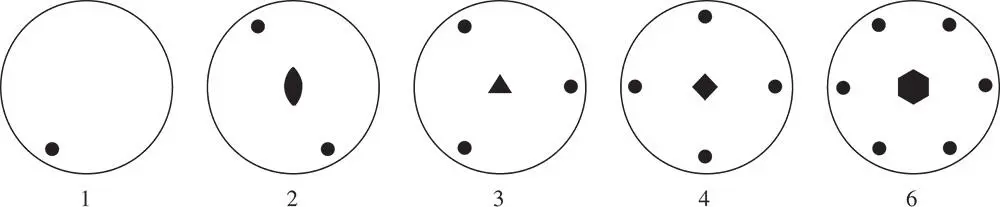
Figure 2.2Stereograms representing the operation of one‐, two‐, three‐, four‐ and sixfold axes on a single initial pole, represented as a dot

Figure 2.3The repetition of an object by a mirror plane, (a) and (b), and by a centre of symmetry, (c)

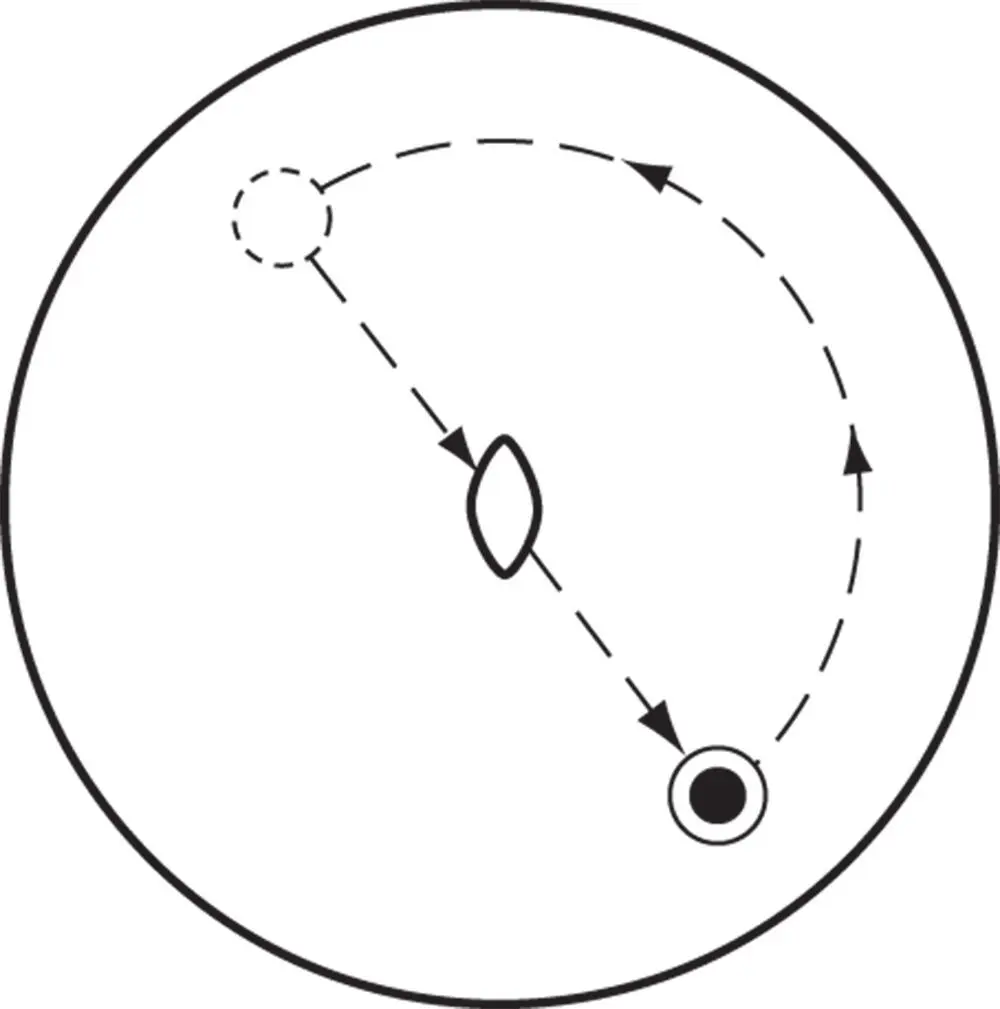
Figure 2.4The operation of the twofold rotoinversion axis,