A lattice consistent with a single threefold rotational axis can be produced by stacking triequiangular nets in a staggered sequence. A unit cell of the triequiangular net of points is shown outlined in Figure 1.26by the vectors t 1, t 2along the x ‐ and y ‐axes. Axes of threefold symmetry pierce the net at the origin of the cell (0, 0) – at points such as A – and also at two positions within the cell with coordinates 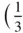 ,
, 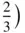 and
and 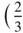 ,
, 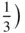 , respectively, which are labelled B and C, respectively in Figure 1.26. We can preserve the threefold symmetry (while of course destroying the sixfold one) by stacking nets so that the extremity of t 3has coordinates of either
, respectively, which are labelled B and C, respectively in Figure 1.26. We can preserve the threefold symmetry (while of course destroying the sixfold one) by stacking nets so that the extremity of t 3has coordinates of either 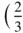 ,
, 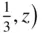 .or
.or 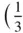 ,
, 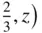 . The two positions B and C in Figure 1.26are equivalent to one another in the sense that the same lattice is produced whatever the order in which these two positions are used.
. The two positions B and C in Figure 1.26are equivalent to one another in the sense that the same lattice is produced whatever the order in which these two positions are used.

Figure 1.26The stacking of triequiangular nets of points in a staggered sequence. Lattice points labelled A, B and C belong to nets of lattice points at different heights relative to the plane of the paper
A plan of the lattice produced, viewed along the triad axis, is shown in Figure 1.27, and a sketch of the relationship between the triequiangular nets and the primitive cells of this lattice is shown in Figure 1.28. In Figures 1.27and 1.28the stacking sequence of the nets has been set as ABCABCABC… Exactly the same lattice but in a different orientation (rotated 60° clockwise looking down upon the paper in Figure 1.27) would have been produced if the sequence ACBACBACB… had been followed. The primitive cell of the trigonal lattice in Figure 1.28is shown in Figure 1.19k. It can be given the symbol R . It is a rhombohedron, the edges of the cell being of equal length, each equally inclined to the single threefold axis. To specify the cell we must state a = b = c and the angle α = β = γ < 120°.
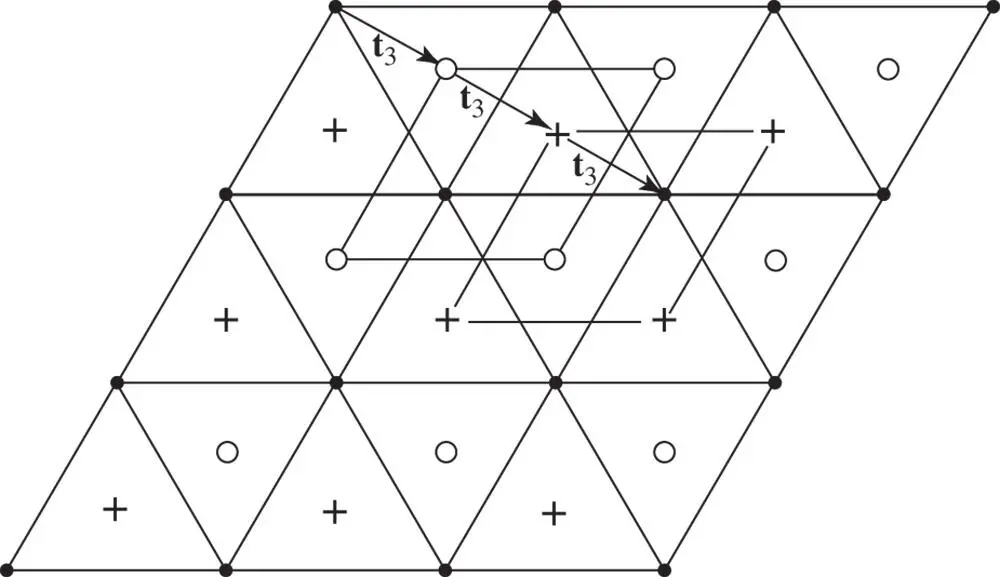
Figure 1.27Lattice points in the net at level zero are marked with a dot, those in the net at height z by an open circle, and those at 2 z by a plus sign. The projection of t 3onto the plane of the nets is shown
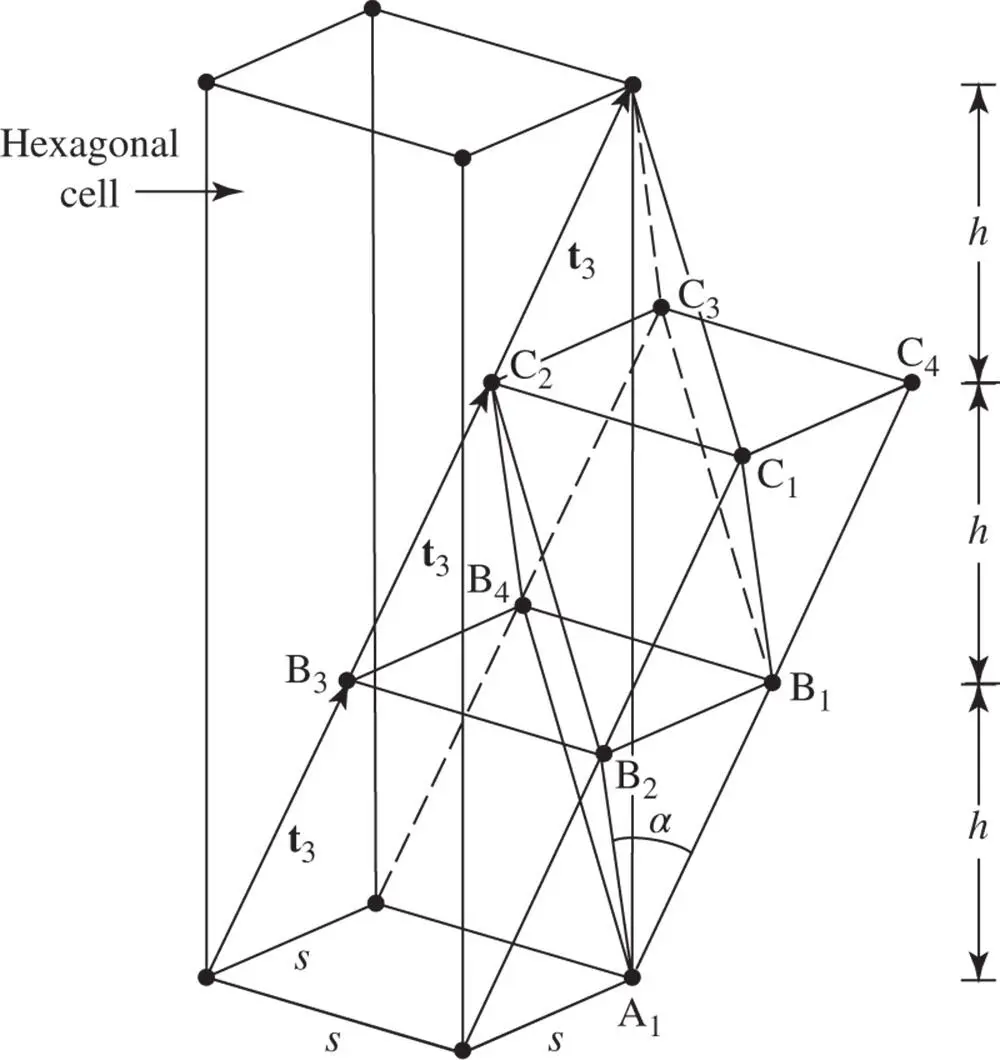
Figure 1.28The relationship between a primitive cell of the trigonal lattice and the triply primitive hexagonal cell
An alternative cell is sometimes used to describe the trigonal lattice R because of the inconvenience in dealing with a lattice of axial angle α , which may take any value between 0 and 120°. The alternative cell is shown in Figure 1.28and in plan viewed along the triad axis in Figure 1.29. It is a triply primitive cell, three mesh layers high, with internal lattice points at elevations of 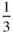 and
and 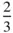 of the repeat distance along the triad axis. The cell is of the same shape as the conventional unit cell of the hexagonal Bravais lattice and to specify it we must know a = b ≠ c , α = β = 90° and γ = 120°.
of the repeat distance along the triad axis. The cell is of the same shape as the conventional unit cell of the hexagonal Bravais lattice and to specify it we must know a = b ≠ c , α = β = 90° and γ = 120°.
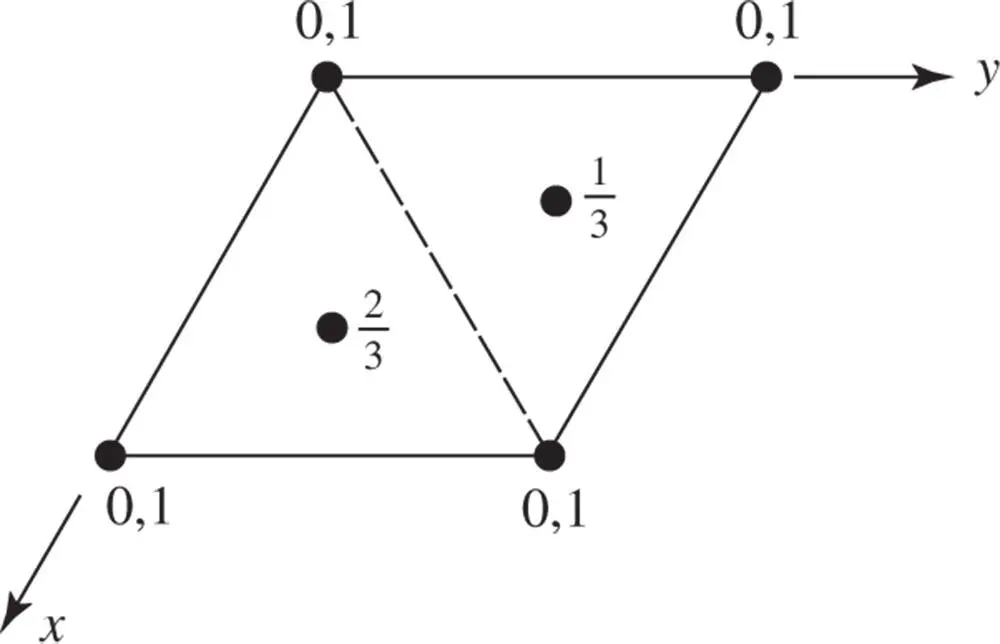
Figure 1.29Plan view of the alternative triply primitive hexagonal unit cell used to describe the trigonal R lattice
Crystals belonging to the cubic system possess four threefold axes of rotational symmetry. The angles between the four threefold axes are such that these threefold axes lie along the body diagonals of a cube ( Figure 1.30), with angles of 70.53° (cos −1(1/3)) between them. Reference to Table 1.2and Figure 1.17b shows that these threefold axes cannot exist alone in a crystal. They must be accompanied by at least three twofold axes. To indicate how the lattices consistent with this arrangement of threefold axes arise, we start with the R lattice shown in Figure 1.28and call the separation of nearest‐neighbour lattice points in the triequiangular net s and the vertical separation of the nets along the triad axis h . The positions of the lattice points in the successive layers when all are projected onto the plane perpendicular to the triad axis can be designated ABCABC… as in Figures 1.26and 1.28. In a trigonal lattice, the spacing of the nets, h , is unrelated to the separation of the lattice points within the nets, s . If we make the spacing of the nets such that h = 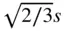 (= 2 s /
(= 2 s / 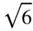 ), the angle α in Figure 1.28becomes 60° and triangles A 1B 1B 2, A 1B 2B 4, A 1B 1B 4all become equilateral. Planes such as A 1B 1C 1B 2, A 1B 2C 2B 4, A 1B 1C 3B 4all contain triequiangular nets of points. Planes parallel to each of these three planes also contain triequiangular nets of points and are also stacked so as to preserve triad symmetry along lines normal to them. When α = 60°, the original trigonal lattice becomes consistent with the possession of four threefold axes. The conventional unit cell of this lattice is shown in Figure 1.19m; it is a cube centred on all faces. The relationship between this cell and the primitive one with α = 60° is shown in Figure 1.31.
), the angle α in Figure 1.28becomes 60° and triangles A 1B 1B 2, A 1B 2B 4, A 1B 1B 4all become equilateral. Planes such as A 1B 1C 1B 2, A 1B 2C 2B 4, A 1B 1C 3B 4all contain triequiangular nets of points. Planes parallel to each of these three planes also contain triequiangular nets of points and are also stacked so as to preserve triad symmetry along lines normal to them. When α = 60°, the original trigonal lattice becomes consistent with the possession of four threefold axes. The conventional unit cell of this lattice is shown in Figure 1.19m; it is a cube centred on all faces. The relationship between this cell and the primitive one with α = 60° is shown in Figure 1.31.
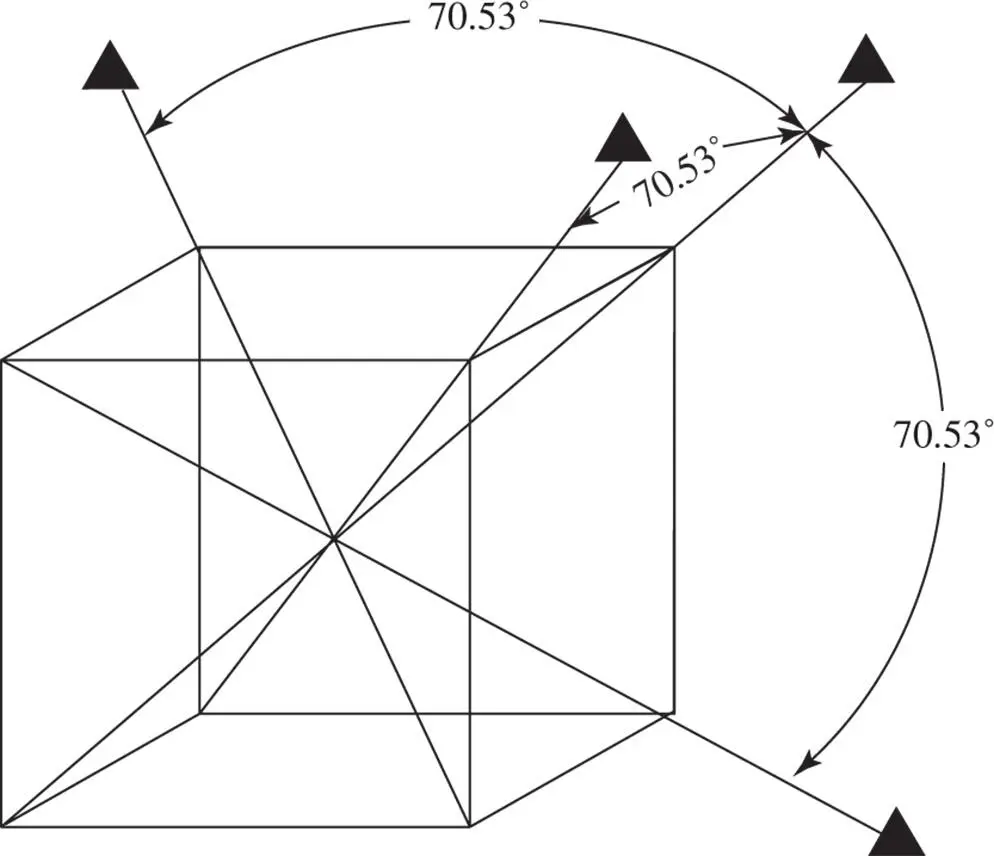
Figure 1.30The four 〈111〉 three‐fold axes with acute angles of 70.53° between one another which together define the minimum symmetry requirements for a crystal to belong to the cubic crystal system
Читать дальше

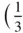 ,
, 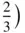 and
and 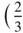 ,
, 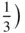 , respectively, which are labelled B and C, respectively in Figure 1.26. We can preserve the threefold symmetry (while of course destroying the sixfold one) by stacking nets so that the extremity of t 3has coordinates of either
, respectively, which are labelled B and C, respectively in Figure 1.26. We can preserve the threefold symmetry (while of course destroying the sixfold one) by stacking nets so that the extremity of t 3has coordinates of either 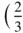 ,
, 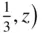 .or
.or 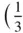 ,
, 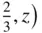 . The two positions B and C in Figure 1.26are equivalent to one another in the sense that the same lattice is produced whatever the order in which these two positions are used.
. The two positions B and C in Figure 1.26are equivalent to one another in the sense that the same lattice is produced whatever the order in which these two positions are used.


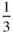 and
and 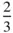 of the repeat distance along the triad axis. The cell is of the same shape as the conventional unit cell of the hexagonal Bravais lattice and to specify it we must know a = b ≠ c , α = β = 90° and γ = 120°.
of the repeat distance along the triad axis. The cell is of the same shape as the conventional unit cell of the hexagonal Bravais lattice and to specify it we must know a = b ≠ c , α = β = 90° and γ = 120°.
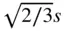 (= 2 s /
(= 2 s / 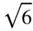 ), the angle α in Figure 1.28becomes 60° and triangles A 1B 1B 2, A 1B 2B 4, A 1B 1B 4all become equilateral. Planes such as A 1B 1C 1B 2, A 1B 2C 2B 4, A 1B 1C 3B 4all contain triequiangular nets of points. Planes parallel to each of these three planes also contain triequiangular nets of points and are also stacked so as to preserve triad symmetry along lines normal to them. When α = 60°, the original trigonal lattice becomes consistent with the possession of four threefold axes. The conventional unit cell of this lattice is shown in Figure 1.19m; it is a cube centred on all faces. The relationship between this cell and the primitive one with α = 60° is shown in Figure 1.31.
), the angle α in Figure 1.28becomes 60° and triangles A 1B 1B 2, A 1B 2B 4, A 1B 1B 4all become equilateral. Planes such as A 1B 1C 1B 2, A 1B 2C 2B 4, A 1B 1C 3B 4all contain triequiangular nets of points. Planes parallel to each of these three planes also contain triequiangular nets of points and are also stacked so as to preserve triad symmetry along lines normal to them. When α = 60°, the original trigonal lattice becomes consistent with the possession of four threefold axes. The conventional unit cell of this lattice is shown in Figure 1.19m; it is a cube centred on all faces. The relationship between this cell and the primitive one with α = 60° is shown in Figure 1.31.











