Anthony Kelly - Crystallography and Crystal Defects

All of the symmetry operations in a crystal must be mutually consistent. There are no fivefold axes of rotational symmetry because such axes are not consistent with the translational symmetry of the lattice. In Section 1.6we derived the possible combinations of pure rotational symmetry operations that can pass through a point. These combinations are classified into different crystal systems and we will now investigate the types of space lattice (that is, the regular arrangement of points in three dimensions as defined in Section 1.1) that are consistent with the various combinations of rotation axes. We shall find, as we did for the two‐dimensional lattice (or net) consistent with mirror symmetry ( Section 1.5), that more than one arrangement of points is consistent with a given set of rotational symmetry operations. However, the number of essentially different arrangements of points is limited to 14. These are the 14 Bravais, or space, lattices. Our derivation is by no means a rigorous one because we do not show that our solutions are unique. This derivation of the Bravais lattices is introduced to provide a background for a clear understanding of the properties of imperfections studied in Part II of this book. The lattice is the most important symmetry concept for the discussion of dislocations and martensitic transformations.

We start with the planar lattices or nets illustrated in Figure 1.14. To build up a space lattice we stack these nets regularly above one another to form an infinite set of parallel sheets of spacing z . All of the sheets are in identical orientation with respect to an axis of rotation normal to their plane, so that corresponding lattice vectors t 1and t 2in the nets are always parallel. The stacking envisaged is shown in Figure 1.18. The vector t 3joining lattice points in adjacent nets is held constant from net to net. The triplet of vectors t 1, t 2, t 3defines a unit cell of the Bravais lattice.

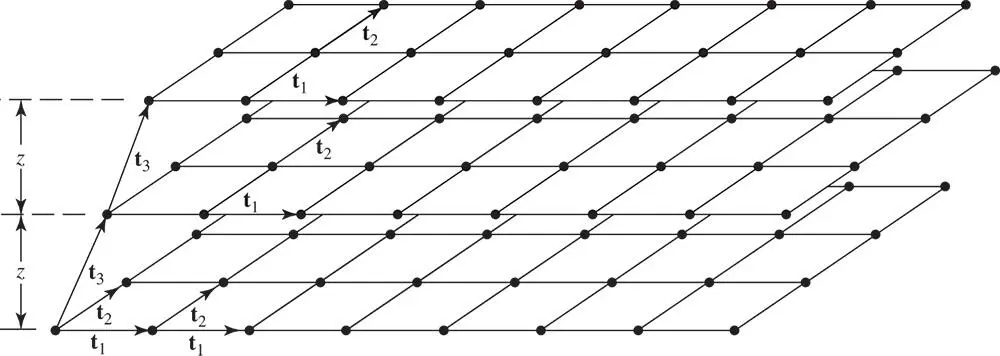
Figure 1.18Stacking of nets to build up a space lattice. The triplet of vectors t 1, t 2, t 3defines a unit cell of the Bravais lattice

We now consider the net based on a parallelogram ( Figure 1.14a). If we stack nets of this form so that the points of intersection of twofold axes in successive nets do not lie vertically above one another then we destroy the twofold symmetry axes normal to the nets. We have a lattice of points showing no rotational symmetry. The unit cell is an arbitrary parallelepiped with edges a , b , c , no two of which are necessarily equal, and where the angles of the unit cell α , β , γ can take any value; the cell is shown in Figure 1.19a. By choosing a , b , c appropriately we can always ensure that the cell is primitive. Although this lattice contains no axis of rotational symmetry, the set of lattice points is of course necessarily centrosymmetric.

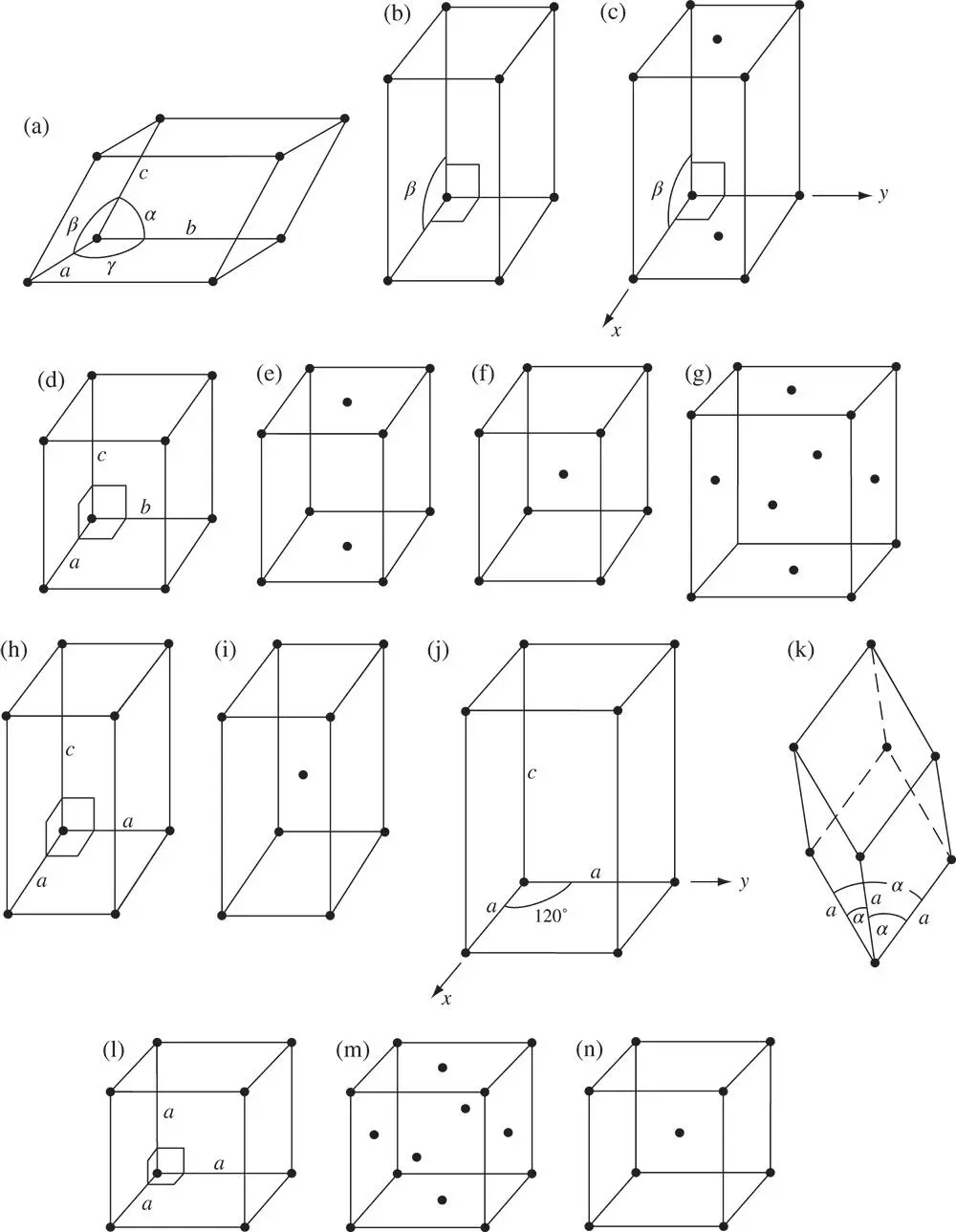
Figure 1.19Unit cells of the 14 Bravais space lattices. (a) Primitive triclinic. (b) Primitive monoclinic. (c) Side‐centred monoclinic – conventionally the twofold axis is taken parallel to y and the (001) face is centred ( C ‐centred). (d) Primitive orthorhombic. (e) Side‐centred orthorhombic – conventionally centred on (001) ( C ‐centred). (f) Body‐centred orthorhombic. (g) Face‐centred orthorhombic. (h) Primitive tetragonal. (i) Body‐centred tetragonal. (j) Primitive hexagonal. (k) Primitive rhombohedral. (l) Primitive cubic. (m) Face‐centred cubic. (n) Body‐centred cubic

To preserve twofold symmetry we can proceed in one of two different ways. We can arrange parallelogram nets vertically above one another so that t 3is normal to the plane of the sheets, as in Figure 1.20a, or we can produce the staggered arrangement shown in plan, viewed perpendicular to the nets, in Figure 1.20b.

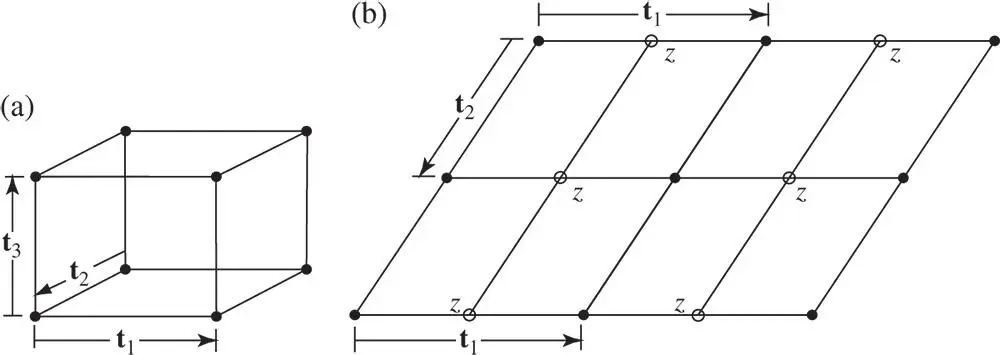
Figure 1.20Lattice points in the net at height zero are marked as dots, those at height z with rings

In the first of these arrangements, in Figure 1.20a, the twofold axes at the corners of the unit parallelogram of the nets all coincide and we produce a lattice of which one unit cell is shown in Figure 1.19b. This has no two sides of the primitive cell necessarily equal, but two of the axial angles are 90°. A frequently used convention is to take α and γ as 90° so that y is normal to x and to z ; β is then taken as the obtuse angle between x and z .

The staggered arrangement of the parallelogram nets in Figure 1.20b is such that the twofold axes at the corners of the unit parallelograms of the second net coincide with those at the centres of the sides of the unit parallelogram of those of the first (or zero‐level) net. A lattice is then produced of which a possible unit cell is shown in Figure 1.21. This is multiply primitive, containing two lattice points per unit cell, and the vector t 4is normal to t 1and t 2. Such a cell with lattice points at the centres of a pair of opposite faces parallel to the diad axis is also consistent with twofold symmetry. The cell centred on opposite faces shown in Figure 1.21is chosen to denote the lattice produced from the staggered nets because it is more naturally related to the twofold symmetry than a primitive unit cell would be for this case.

Figure 1.21A three‐dimensional view of the staggered arrangement of nets in Figure 1.20(b) in which two‐fold symmetry is preserved. In this diagram, the vector t 4is normal to t 1and t 2

The staggered arrangement of nets shown in Figures 1.20b and 1.21could also have shown diad symmetry if we had arranged that the corners of the net at height z had lain not above the midpoints of the side containing t 1in Figure 1.20b but vertically above either the centre of the unit parallelogram of the first net or above the centre of the side containing t 2in Figure 1.20b. These two staggered arrangements are not essentially different from the first one, since, as is apparent from Figure 1.22, a new choice of axes in the plane of the nets is all that is needed to make them completely equivalent.

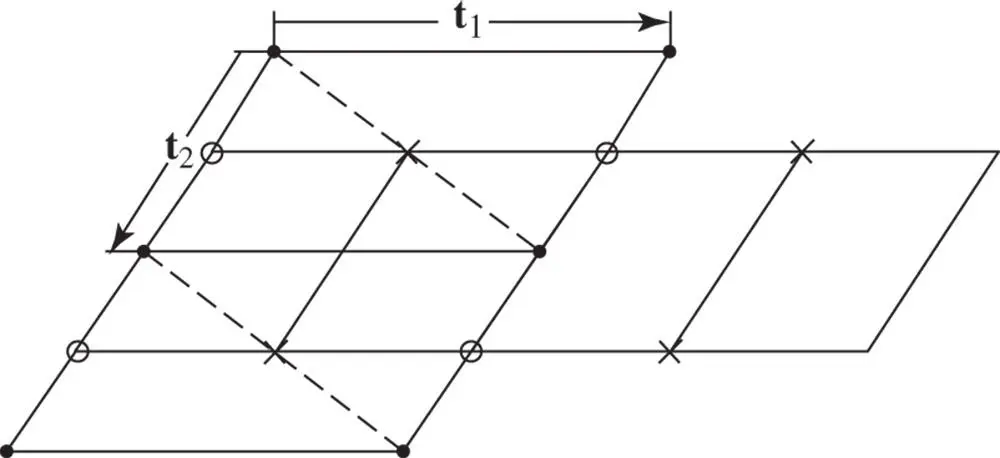
Figure 1.22Lattice points in the net at height zero are marked with dots. The rings and crosses indicate alternative positions of the lattice points in staggered nets at height z , arranged so as to preserve twofold symmetry. The dotted lines show an alternative choice of unit cell

There are then two lattices consistent with monoclinic symmetry: the primitive one with the unit cell shown in Figure 1.19b and a lattice made up from staggered nets of which the conventional unit cell is centred on a pair of opposite faces. The centred faces are conventionally taken as the faces parallel to the x ‐ and y ‐axes; that is, (001), with the diad parallel to y (see Figure 1.19c). This lattice is called the monoclinic C lattice. The two lattices in the monoclinic system can be designated P and C , respectively.