To plot a stereogram of an orthorhombic crystal centred on 001 if we are given the lattice parameters a, b and c , we proceed as shown in Figure 2.8. In Figure 2.8a the poles of the (001), (010) and (100) planes are immediately inserted at the centre of the primitive and where the x ‐ and y ‐axes cut the primitive, respectively. A pole ( hk 0) can be inserted at an angle θ along the primitive to (100), as shown in Figure 2.8a, by noting from Figure 2.8b (which is a section of the crystal parallel to (001) showing the intersection of the plane ( hk 0) with the crystal axes) that the pole of (100) lies along OM , that ( hk 0) makes intercepts on the crystal axes of a/h along the x ‐axis and b/k along the y ‐axis, and that θ is the angle between the normal to ( hk 0) and the normal to (100). From Figure 2.8b we have:
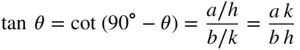
That is:
(2.1a) 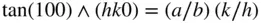
where (100) ∧( hk 0) means the angle between the (100) and ( hk 0) planes; that is, the angle between the pole of (100) and the pole of ( hk 0). Similarly, if the lattice parameters are given, we can locate (0 kl ) and ( h 0 l ), since:
(2.1b) 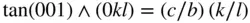
and:
(2.1c) 
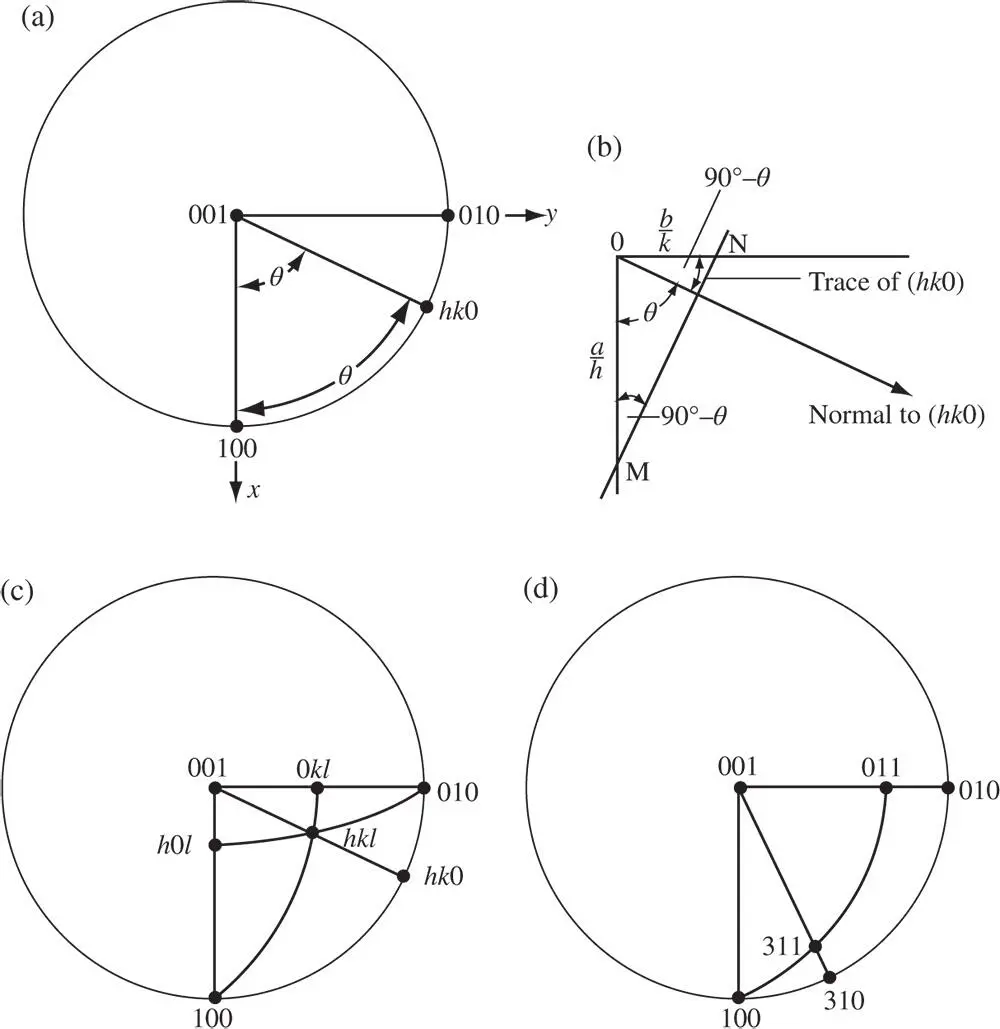
Figure 2.8(a) General location of a hk 0 pole on the stereogram of an orthorhombic crystal, (b) geometry to determine the angle θ between the 100 pole and the hk 0 pole, (c) location of the hkl pole given the locations of the hk 0, h 0 l and 0 kl poles, (d) the location of the 311 pole given the locations of the 100, 010, 001, 011 and 310 poles
These relations can be seen immediately by drawing diagrams similar to Figure 2.8b but looking along the x ‐ and y ‐axes, respectively. When poles such as ( h 0 l ), (0 kl ) and ( hk 0) have been inserted on the stereogram, we can insert a pole such as ( hkl ) immediately by use of the zone addition rule, given in Section 1.3, Eq. (1.20).
If two poles ( h 1 k 1 l 1), ( h 2 k 2 l 2) both lie in the same zone with the indices [ uvw ] then so does the pole of the plane ( mh 1+ nh 2, mk 1+ nk 2, ml 1+ nl 2); that is, any plane whose indices can be formed by taking linear combinations of the indices of two planes in a given zone can provide the indices of a further plane in that same zone ( Section 1.3). In general, m and n can be positive or negative, but if m and n are both positive then the pole of the plane under consideration must lie on the great circle between the poles of ( h 1 k 1 l 1) and ( h 2 k 2 l 2): this simple result can be extremely useful when locating poles on stereographic projections such as Figure 2.7.
In Figure 2.8c, after (001), (010), (100) and ( hk 0), ( h 0 l ), (0 kl ) are plotted, then to plot, say, ( hkl ), we note that ( hkl ) must lie in the zone containing (001) and ( hk 0), since if we multiply (001) by the number l and add the indices (00 l ) and ( hk 0) we obtain ( hkl ). It then follows that ( hkl ) lies somewhere on the great circle between (001) and ( hk 0). Similarly, ( hkl ) lies in the zone containing (0 kl ) and (100), since h times (100) gives ( h 00) and this added to (0 kl ) gives ( hkl ). Again, it is true that ( hkl ) lies somewhere on the great circle between (0 kl ) and (100), but we can now rationalize that ( hkl ) must lie at the intersection of the two great circles we have considered. We then draw the great circle (or zone) containing (001) and ( hk 0) and that containing (001) and (0 kl ) and we know that ( hkl ) is situated where these intersect.
A particular example may make the procedure clear. Suppose we wish to locate (311) after plotting (001), (010) and (100) ( Figure 2.8d). One way to proceed would be to locate (011) using Eq.(2.1b), setting k = 1 and l = 1 and using the known lattice parameters. We then find (310), on the primitive, by finding the angle between (100) and (310) from Eq.(2.1a), setting h = 3 and k = 1. Finally, we note that (311) lies in the zone containing (001) and (310), since (001) plus (310) yields (311). Also, (311) lies in the zone containing (100) and (011) since three times (100) plus (011) yields (311). The pole of (311) is then immediately located by drawing the great circle through (001) and (310) and that through (011) and (100); (311) is located where these great circles meet.
Using the above procedure for locating poles is usually the quickest way to draw an accurate stereogram when key poles have been located either by calculation or through the use of a computer software package. It must be strongly emphasized that, although we have chosen the orthorhombic system as an example, the use of Eq. (1.20) to locate poles applies to any crystal system and does not depend on the crystal axes being at any particular angle to one another. The utility of Eq. (1.20) is one of the great advantages of the Miller index for denoting crystal planes, and arises naturally from the properties of a space lattice.
Equations such as those in Eq. (2.1) can of course be used to find the ratio of the lattice parameters – the axial ratios – from measurements of the angles between poles.
The tetrad axis is always taken parallel to the z ‐axis. The lattice parameters a and b are equal.
The holosymmetric point group is 4/ mmm , showing three mutually perpendicular mirror planes with a tetrad normal to one of them ( Figure 2.6). If a single pole is repeated according to the presence of these symmetry elements it will be found that diad axes are necessarily present normal to the mirrors and that, in addition, a second pair of diad axes also normal to mirror planes automatically arises. One of the pairs of mutually perpendicular diads is chosen as defining the directions of the x ‐ and y ‐axes. The general form is { hkl }, with a multiplicity of 16. Special forms are {001}, {100}, {110}, { hk 0}, { h 0 l } and { hhl }. The last of these, { hhl }, indicates a face making equal intercepts on the x ‐ and y ‐axes.
The point group 422 could be specified simply as 42 since if 4 and 2 are present at right angles a second pair of diad axes arises and one of these pairs is chosen to define the x ‐ and y ‐axes. The group 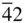 m can be developed as
m can be developed as 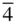 m . It is then found that diad axes automatically arise at 45° to the two, mutually perpendicular, mirror planes. The pair of diad axes is taken to define the x ‐ and y ‐axes. The four other tetragonal point groups, 4,
m . It is then found that diad axes automatically arise at 45° to the two, mutually perpendicular, mirror planes. The pair of diad axes is taken to define the x ‐ and y ‐axes. The four other tetragonal point groups, 4, 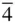 , 4/ m and 4 mm , are straightforward and no diad axes arise.
, 4/ m and 4 mm , are straightforward and no diad axes arise.
Читать дальше

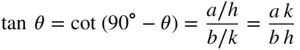
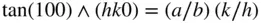
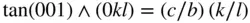


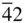 m can be developed as
m can be developed as 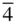 m . It is then found that diad axes automatically arise at 45° to the two, mutually perpendicular, mirror planes. The pair of diad axes is taken to define the x ‐ and y ‐axes. The four other tetragonal point groups, 4,
m . It is then found that diad axes automatically arise at 45° to the two, mutually perpendicular, mirror planes. The pair of diad axes is taken to define the x ‐ and y ‐axes. The four other tetragonal point groups, 4,  , 4/ m and 4 mm , are straightforward and no diad axes arise.
, 4/ m and 4 mm , are straightforward and no diad axes arise.










