The angles between poles on a stereogram and the ratio of the lattice parameters (i.e. the ratio a : c in this crystal system) are easily related by using equations such as those in Eq. (2.1) with a = b .
Cubic crystals possess four triad axes as a minimum symmetry requirement. These are arranged as in Figure 1.30and are always taken to lie along the 〈111〉 type directions of the unit cell, which is a cube, so a = b = c . This is the only crystal system in which the direction [ uvw ] necessarily coincides with the normal to the plane ( uvw ) for all u , v , w .
If we put four triad axes to coincide with the 〈111〉 directions on a stereogram and allow these to operate on a single pole, as in Figure 2.9, we find that diad axes automatically arise along the crystal axes. The presence of the diads also follows from Table 1.2, with the row starting 233. The point group symbol used to describe the combination of a diad and two triads, shown in Table 1.2, is just 23. This is the cubic point group of lowest symmetry. The multiplicity of the general form for this point group is 12 ( Figure 2.9). A feature of the symbols for describing point groups in the cubic system is that the symbol 3 or 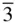 , even though it indicates the defining axis for the system, is never placed first because the triads, or inverse triads, are always at 54.74° (cos −1(1/
, even though it indicates the defining axis for the system, is never placed first because the triads, or inverse triads, are always at 54.74° (cos −1(1/ 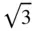 )) to the crystal axes. (In all other systems the defining axis comes first in the symbol – the presence of the diads or inverse diads parallel to at least two axes must be stated to distinguish orthorhombic point groups from monoclinic point groups.)
)) to the crystal axes. (In all other systems the defining axis comes first in the symbol – the presence of the diads or inverse diads parallel to at least two axes must be stated to distinguish orthorhombic point groups from monoclinic point groups.)
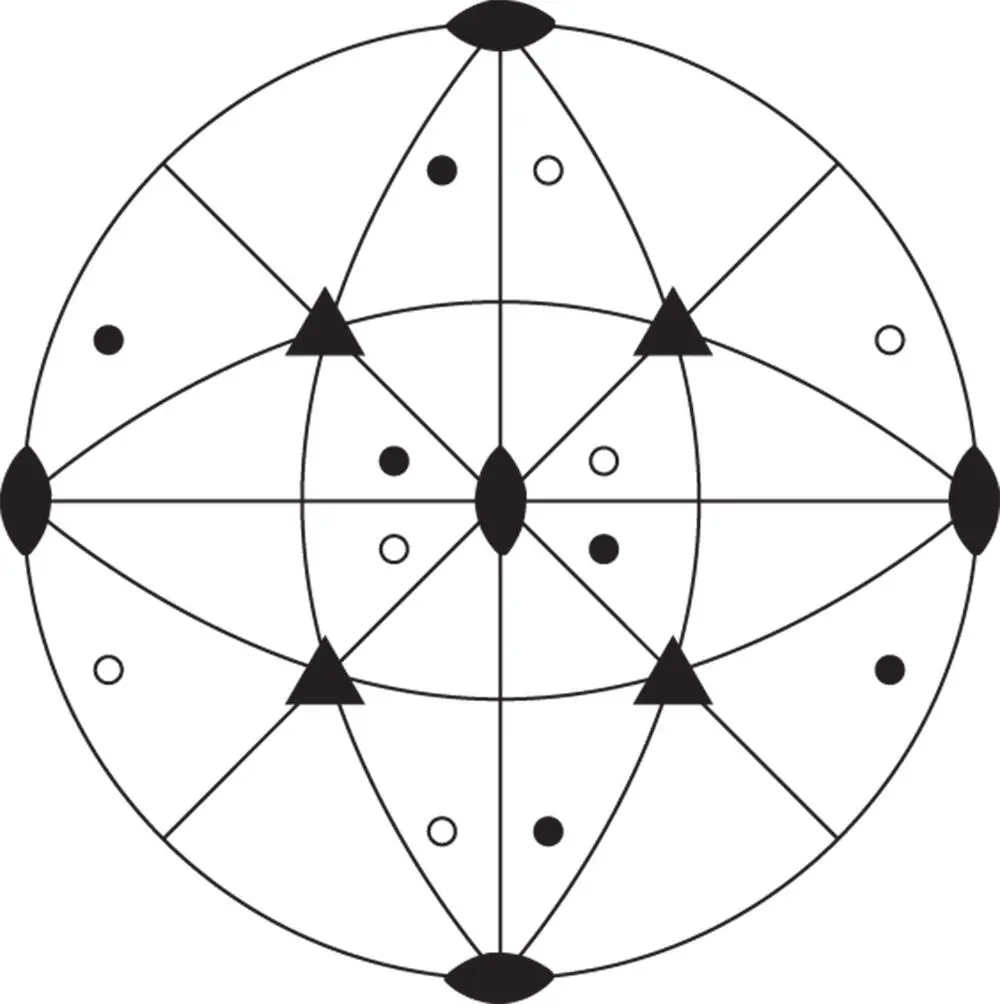
Figure 2.9The cubic point group of lowest symmetry: 23
The figure 3 (or 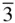 ) always occurs second in the symbol for cubic point groups, and this enables a point group in the cubic system to be distinguished from those in all other crystal systems. In a cubic crystal, mirror planes can run either parallel to {100} planes, as in Figure 2.10a, or else parallel to {110} planes, as in Figure 2.10b. The first alternative is described by putting the symbol m before
) always occurs second in the symbol for cubic point groups, and this enables a point group in the cubic system to be distinguished from those in all other crystal systems. In a cubic crystal, mirror planes can run either parallel to {100} planes, as in Figure 2.10a, or else parallel to {110} planes, as in Figure 2.10b. The first alternative is described by putting the symbol m before 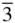 (to give m
(to give m 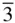 ) and the second by placing m after the 3 (or
) and the second by placing m after the 3 (or 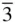 ) to give X 3 m or X
) to give X 3 m or X 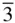 m , where X is an axis other than 3 or
m , where X is an axis other than 3 or 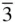 .
.
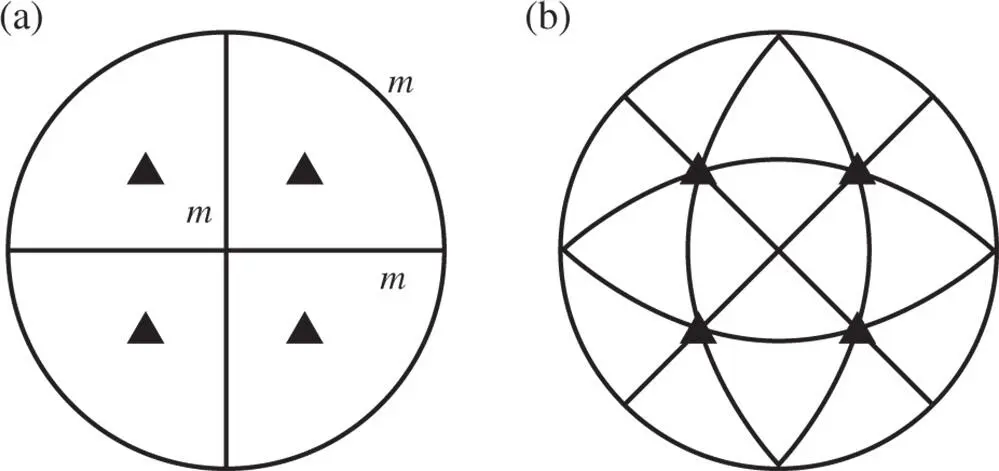
Figure 2.10Stereograms centred on 001 of (a) mirror planes parallel to {100} planes and (b) mirror planes parallel to {110} planes in a cubic crystal. In both (a) and (b) the location of the four triads are shown; these are the minimum symmetry requirement for cubic crystals
If we add mirror planes parallel to {100} to the class 23 we obtain 2/ m 3, conventionally denoted m 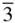 . (Prior to the revision of the International Tables for Crystallography in 1995 this point group was denoted m 3; older textbooks will use this terminology as well.) As is evident from Figure 2.6, this contains a centre of symmetry in addition to the three diads at the intersection of three mutually perpendicular mirror planes and the four triads. The triads therefore become inversion triads,
. (Prior to the revision of the International Tables for Crystallography in 1995 this point group was denoted m 3; older textbooks will use this terminology as well.) As is evident from Figure 2.6, this contains a centre of symmetry in addition to the three diads at the intersection of three mutually perpendicular mirror planes and the four triads. The triads therefore become inversion triads, 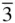 . The multiplicity of the general form { hkl } is 24. It is worth noting from Table 2.3(see below) that when there are no diads along 〈110〉 directions nor mirrors parallel to {110}, { hk 0} and { kh 0} are separate special forms. This occurs in the classes 23 and m
. The multiplicity of the general form { hkl } is 24. It is worth noting from Table 2.3(see below) that when there are no diads along 〈110〉 directions nor mirrors parallel to {110}, { hk 0} and { kh 0} are separate special forms. This occurs in the classes 23 and m 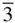 .
.
Replacement of the diads in 23 by tetrads gives 43. Here we notice that diads automatically arise along the 〈110〉 directions, as tabulated in Table 1.2. This class is denoted 432 to indicate the diads because of later development of space groups (see Section 2.11). However, 43 is sufficient to identify it.
Replacement of 2 by 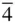 in 23 will be found to produce mirror planes automatically parallel to the {110} planes, and hence passing through the triads. Correspondingly, if mirrors parallel to {110} are added to 23 then the diad axes along the 〈100〉 directions become
in 23 will be found to produce mirror planes automatically parallel to the {110} planes, and hence passing through the triads. Correspondingly, if mirrors parallel to {110} are added to 23 then the diad axes along the 〈100〉 directions become 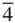 axes. If we have mirror planes passing through the triad axes then parallel to the crystal axes we can have either
axes. If we have mirror planes passing through the triad axes then parallel to the crystal axes we can have either 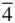 or 4. The first of these classes is
or 4. The first of these classes is 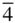 3 m and the second m
3 m and the second m 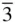 m . (This latter point group was known as m 3 m conventionally prior to the 1995 revision of the International Tables for Crystallography .) In
m . (This latter point group was known as m 3 m conventionally prior to the 1995 revision of the International Tables for Crystallography .) In 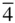 3 m there is no centre of symmetry and there are no additional symmetry elements, other than those indicated in the symbol. The multiplicity of the general form is 24. In
3 m there is no centre of symmetry and there are no additional symmetry elements, other than those indicated in the symbol. The multiplicity of the general form is 24. In 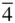 3 m (as in 23), {111} and {1
3 m (as in 23), {111} and {1  1} are separate special forms: each shows four planes parallel to the surfaces of a regular tetrahedron.
1} are separate special forms: each shows four planes parallel to the surfaces of a regular tetrahedron.
Class m 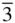 m has mirror planes parallel to {100} and to {110}; therefore, nine mirror planes are present in all. There are six diads, three tetrads, a centre and of course the four triads. All of these can be produced by putting mirrors parallel to both {110} and {100}, coupled with the four triads. Hence the symbol m
m has mirror planes parallel to {100} and to {110}; therefore, nine mirror planes are present in all. There are six diads, three tetrads, a centre and of course the four triads. All of these can be produced by putting mirrors parallel to both {110} and {100}, coupled with the four triads. Hence the symbol m 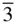 m is used to describe this point group, which is the cubic holosymmetric class. In full notation this would be 4/ m
m is used to describe this point group, which is the cubic holosymmetric class. In full notation this would be 4/ m 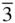 2/ m , to denote the point group symmetry elements as 4/ m along the 〈100〉 directions,
2/ m , to denote the point group symmetry elements as 4/ m along the 〈100〉 directions, 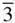 along the 〈111〉 directions and 2/ m along the 〈110〉 directions. The general form has 48 faces.
along the 〈111〉 directions and 2/ m along the 〈110〉 directions. The general form has 48 faces.
Читать дальше

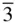 , even though it indicates the defining axis for the system, is never placed first because the triads, or inverse triads, are always at 54.74° (cos −1(1/
, even though it indicates the defining axis for the system, is never placed first because the triads, or inverse triads, are always at 54.74° (cos −1(1/ 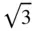 )) to the crystal axes. (In all other systems the defining axis comes first in the symbol – the presence of the diads or inverse diads parallel to at least two axes must be stated to distinguish orthorhombic point groups from monoclinic point groups.)
)) to the crystal axes. (In all other systems the defining axis comes first in the symbol – the presence of the diads or inverse diads parallel to at least two axes must be stated to distinguish orthorhombic point groups from monoclinic point groups.)
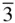 ) always occurs second in the symbol for cubic point groups, and this enables a point group in the cubic system to be distinguished from those in all other crystal systems. In a cubic crystal, mirror planes can run either parallel to {100} planes, as in Figure 2.10a, or else parallel to {110} planes, as in Figure 2.10b. The first alternative is described by putting the symbol m before
) always occurs second in the symbol for cubic point groups, and this enables a point group in the cubic system to be distinguished from those in all other crystal systems. In a cubic crystal, mirror planes can run either parallel to {100} planes, as in Figure 2.10a, or else parallel to {110} planes, as in Figure 2.10b. The first alternative is described by putting the symbol m before 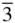 (to give m
(to give m 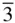 ) and the second by placing m after the 3 (or
) and the second by placing m after the 3 (or 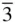 ) to give X 3 m or X
) to give X 3 m or X 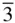 m , where X is an axis other than 3 or
m , where X is an axis other than 3 or 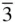 .
.
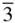 . (Prior to the revision of the International Tables for Crystallography in 1995 this point group was denoted m 3; older textbooks will use this terminology as well.) As is evident from Figure 2.6, this contains a centre of symmetry in addition to the three diads at the intersection of three mutually perpendicular mirror planes and the four triads. The triads therefore become inversion triads,
. (Prior to the revision of the International Tables for Crystallography in 1995 this point group was denoted m 3; older textbooks will use this terminology as well.) As is evident from Figure 2.6, this contains a centre of symmetry in addition to the three diads at the intersection of three mutually perpendicular mirror planes and the four triads. The triads therefore become inversion triads, 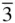 . The multiplicity of the general form { hkl } is 24. It is worth noting from Table 2.3(see below) that when there are no diads along 〈110〉 directions nor mirrors parallel to {110}, { hk 0} and { kh 0} are separate special forms. This occurs in the classes 23 and m
. The multiplicity of the general form { hkl } is 24. It is worth noting from Table 2.3(see below) that when there are no diads along 〈110〉 directions nor mirrors parallel to {110}, { hk 0} and { kh 0} are separate special forms. This occurs in the classes 23 and m 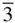 .
.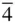 in 23 will be found to produce mirror planes automatically parallel to the {110} planes, and hence passing through the triads. Correspondingly, if mirrors parallel to {110} are added to 23 then the diad axes along the 〈100〉 directions become
in 23 will be found to produce mirror planes automatically parallel to the {110} planes, and hence passing through the triads. Correspondingly, if mirrors parallel to {110} are added to 23 then the diad axes along the 〈100〉 directions become 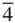 axes. If we have mirror planes passing through the triad axes then parallel to the crystal axes we can have either
axes. If we have mirror planes passing through the triad axes then parallel to the crystal axes we can have either 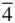 or 4. The first of these classes is
or 4. The first of these classes is 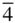 3 m and the second m
3 m and the second m 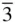 m . (This latter point group was known as m 3 m conventionally prior to the 1995 revision of the International Tables for Crystallography .) In
m . (This latter point group was known as m 3 m conventionally prior to the 1995 revision of the International Tables for Crystallography .) In 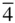 3 m there is no centre of symmetry and there are no additional symmetry elements, other than those indicated in the symbol. The multiplicity of the general form is 24. In
3 m there is no centre of symmetry and there are no additional symmetry elements, other than those indicated in the symbol. The multiplicity of the general form is 24. In 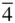 3 m (as in 23), {111} and {1
3 m (as in 23), {111} and {1  1} are separate special forms: each shows four planes parallel to the surfaces of a regular tetrahedron.
1} are separate special forms: each shows four planes parallel to the surfaces of a regular tetrahedron.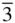 m has mirror planes parallel to {100} and to {110}; therefore, nine mirror planes are present in all. There are six diads, three tetrads, a centre and of course the four triads. All of these can be produced by putting mirrors parallel to both {110} and {100}, coupled with the four triads. Hence the symbol m
m has mirror planes parallel to {100} and to {110}; therefore, nine mirror planes are present in all. There are six diads, three tetrads, a centre and of course the four triads. All of these can be produced by putting mirrors parallel to both {110} and {100}, coupled with the four triads. Hence the symbol m 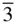 m is used to describe this point group, which is the cubic holosymmetric class. In full notation this would be 4/ m
m is used to describe this point group, which is the cubic holosymmetric class. In full notation this would be 4/ m 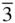 2/ m , to denote the point group symmetry elements as 4/ m along the 〈100〉 directions,
2/ m , to denote the point group symmetry elements as 4/ m along the 〈100〉 directions, 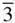 along the 〈111〉 directions and 2/ m along the 〈110〉 directions. The general form has 48 faces.
along the 〈111〉 directions and 2/ m along the 〈110〉 directions. The general form has 48 faces.










