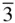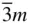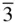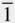The great circle passing through 001 and 010 is the [100] zone, containing planes of the general form (0 kl ). Therefore, the angle between this zone and the primitive must be the angle between [100] and [001], β , as shown in Figure 2.21a. This is because the stereographic projection is a conformal projection (see Appendix 2); that is, one for which angles are faithfully reproduced. Similarly, α and γ can be specified on Figure 2.21a from the triclinic system geometry.
Angles between poles can be determined using Eq. (A3.18). Once the position of the 010 pole (or any other pole of the form hk 0) has been chosen, geometry determines the positions of the remaining poles on the stereogram. Thus, for example, the position of the 001 pole is fixed knowing that it lies in the [100] zone, which has to make an angle of β with the primitive, and that 001 is a given angle from 010, determined for example using Eq. (A3.18). Likewise, the position of a pole 0 kl lying in the [100] zone can be determined, as can the positions of the poles 100, h 0 l , hk 0 and hkl .
While stereographic projections can now be produced routinely via proprietary software packages, it is still instructive to consider further aspects of the geometry of the part of the triclinic stereogram shown in Figure 2.21a in order to gain a full appreciation of the richness of information displayed on stereograms. An ( hkl ) plane of a triclinic crystal is shown in Figure 2.21b. The six angles φ 1– φ 6in Figure 2.21b are the same as those marked in Figure 2.21a.
Thus, for example, φ 1in Figure 2.21b is an angle lying in the (001) plane. It is the angle between the y ‐axis and the vector [ 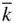 h 0] common to ( hkl ) and (001); that is, the angle between the zone containing (001), ( h 0 l ) and (100) and the zone containing (001), ( hkl ) and ( hk 0). We can therefore mark φ 1on the stereogram. Similarly, φ 5in Figure 2.21b is an angle lying in the (100) plane. It is the angle between the z ‐axis and the vector [0
h 0] common to ( hkl ) and (001); that is, the angle between the zone containing (001), ( h 0 l ) and (100) and the zone containing (001), ( hkl ) and ( hk 0). We can therefore mark φ 1on the stereogram. Similarly, φ 5in Figure 2.21b is an angle lying in the (100) plane. It is the angle between the z ‐axis and the vector [0 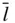 k ] common to ( hkl ) and (100); that is, the angle between the zone containing (100), ( hk 0) and (010) and the zone containing (100), ( hkl ) and (0 kl ). φ 5can therefore also be marked on the stereogram. Proceeding in this way, we can identify all of the angles φ 1– φ 6. We have, from the geometry in Figure 2.21b:
k ] common to ( hkl ) and (100); that is, the angle between the zone containing (100), ( hk 0) and (010) and the zone containing (100), ( hkl ) and (0 kl ). φ 5can therefore also be marked on the stereogram. Proceeding in this way, we can identify all of the angles φ 1– φ 6. We have, from the geometry in Figure 2.21b:
(2.10) 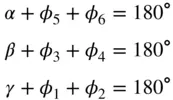
Furthermore, from the triangle on the (001) face in Figure 2.21b we have, using the sine rule:
(2.11) 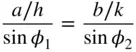
Therefore:
(2.12a) 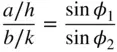
and similarly:
(2.12b) 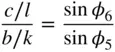
and:
(2.12c) 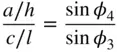
As an aside, we note that the equations in Eq. (2.12)are also of use in finding axial ratios and axial angles from measured angles between planes on single crystal specimens of crystals belonging to the triclinic crystal system; such crystals tend to be minerals or organic materials, rather than metals, the crystal structures of which rarely tend to belong to either the monoclinic or the triclinic systems.
2.9 Special Forms in the Crystal Classes
A summary of the special forms in the various crystal classes for the various crystal systems is given in Table 2.1. The orientation of the axes is that used in this chapter. Monoclinic crystals are in the 2nd setting of Figure 2.6and trigonal crystals are referred to hexagonal axes. There are no special forms in the triclinic system.
2.10 Enantiomorphous Crystal Classes
In some crystal classes the possibility exists of crystals being found in either a right‐handed or a left‐handed modification with the two not being superposable, in the sense that the right hand of the body cannot be superposed upon the left hand. This occurs if the crystal only possesses simple rotation symmetry operations; that is, no symmetry operation of the second kind. Therefore, mirror planes and rotoinversion axes of any degree do not appear in such crystal classes. There are 11 of these classes: 1, 2, 3, 4, 6, 23, 222, 32, 422, 622 and 432.
Some physical methods of examination of crystals cannot determine whether or not there is a centre of symmetry present, such as when stationary single crystals are illuminated by a continuous distribution of X‐ray wavelengths (known as ‘white radiation’) to produce Laue diffraction patterns. This is known as the Laue method. Such diffraction patterns are used for symmetry determination and for the accurate alignment of crystals; they are also useful for time‐resolved macromolecular crystallography using synchrotron radiation. The Laue group is the crystal class to which a particular crystal belongs if a centre of symmetry is added to the symmetry elements already present. The 11 Laue groups are shown in Table 2.2. The loss of symmetry information in time‐resolved macromolecular crystallography is more than compensated for by the ability to capture structural information over subnanosecond timescales in fast chemical reactions such as enzyme reactions.
Table 2.2Laue groups
| System |
Class |
Laue group |
| Cubic |
432,  3 m, 3 m, 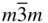 23, 23, 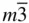 |
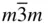 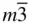 |
| Hexagonal |
622, 6 mm , 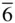 m 2, 6/ mmm 6, m 2, 6/ mmm 6, 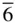 , 6/ m , 6/ m |
6/ mmm 6/ m |
| Tetragonal |
422, 4 mm , 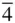 m 2, 4/ mmm 4, m 2, 4/ mmm 4, 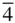 , 4/ m , 4/ m |
4/ mmm 4/ m |
| Trigonal |
32, 3 m , 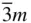 3, 3, 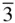 |
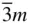 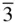 |
| Orthorhombic |
222, 2 mm , mmm |
mmm |
| Monoclinic |
2, m , 2/ m |
2/ m |
| Triclinic |
1, 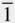 |
 |
Читать дальше

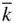 h 0] common to ( hkl ) and (001); that is, the angle between the zone containing (001), ( h 0 l ) and (100) and the zone containing (001), ( hkl ) and ( hk 0). We can therefore mark φ 1on the stereogram. Similarly, φ 5in Figure 2.21b is an angle lying in the (100) plane. It is the angle between the z ‐axis and the vector [0
h 0] common to ( hkl ) and (001); that is, the angle between the zone containing (001), ( h 0 l ) and (100) and the zone containing (001), ( hkl ) and ( hk 0). We can therefore mark φ 1on the stereogram. Similarly, φ 5in Figure 2.21b is an angle lying in the (100) plane. It is the angle between the z ‐axis and the vector [0 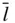 k ] common to ( hkl ) and (100); that is, the angle between the zone containing (100), ( hk 0) and (010) and the zone containing (100), ( hkl ) and (0 kl ). φ 5can therefore also be marked on the stereogram. Proceeding in this way, we can identify all of the angles φ 1– φ 6. We have, from the geometry in Figure 2.21b:
k ] common to ( hkl ) and (100); that is, the angle between the zone containing (100), ( hk 0) and (010) and the zone containing (100), ( hkl ) and (0 kl ). φ 5can therefore also be marked on the stereogram. Proceeding in this way, we can identify all of the angles φ 1– φ 6. We have, from the geometry in Figure 2.21b: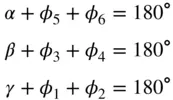
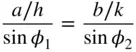
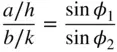
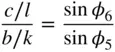
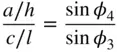
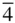 3 m,
3 m, 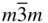 23,
23, 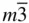
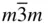
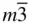
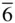 m 2, 6/ mmm 6,
m 2, 6/ mmm 6, 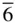 , 6/ m
, 6/ m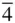 m 2, 4/ mmm 4,
m 2, 4/ mmm 4, 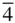 , 4/ m
, 4/ m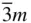 3,
3,