2.13 The 17 Two‐Dimensional Space Groups
The essential elements of how the assignment of a crystal structure to a particular space group imposes restrictions on the possible general and special positions of atoms or ions within a particular unit cell can be illustrated by considering the 17 two‐dimensional space groups (or plane groups). These space groups are shown in Figure 2.24in a manner similar to how they are depicted in the International Tables for Crystallography [3]. If the plane groups are understood, the essential elements of the three‐dimensional space group tables in the International Tables can be understood without difficulty.
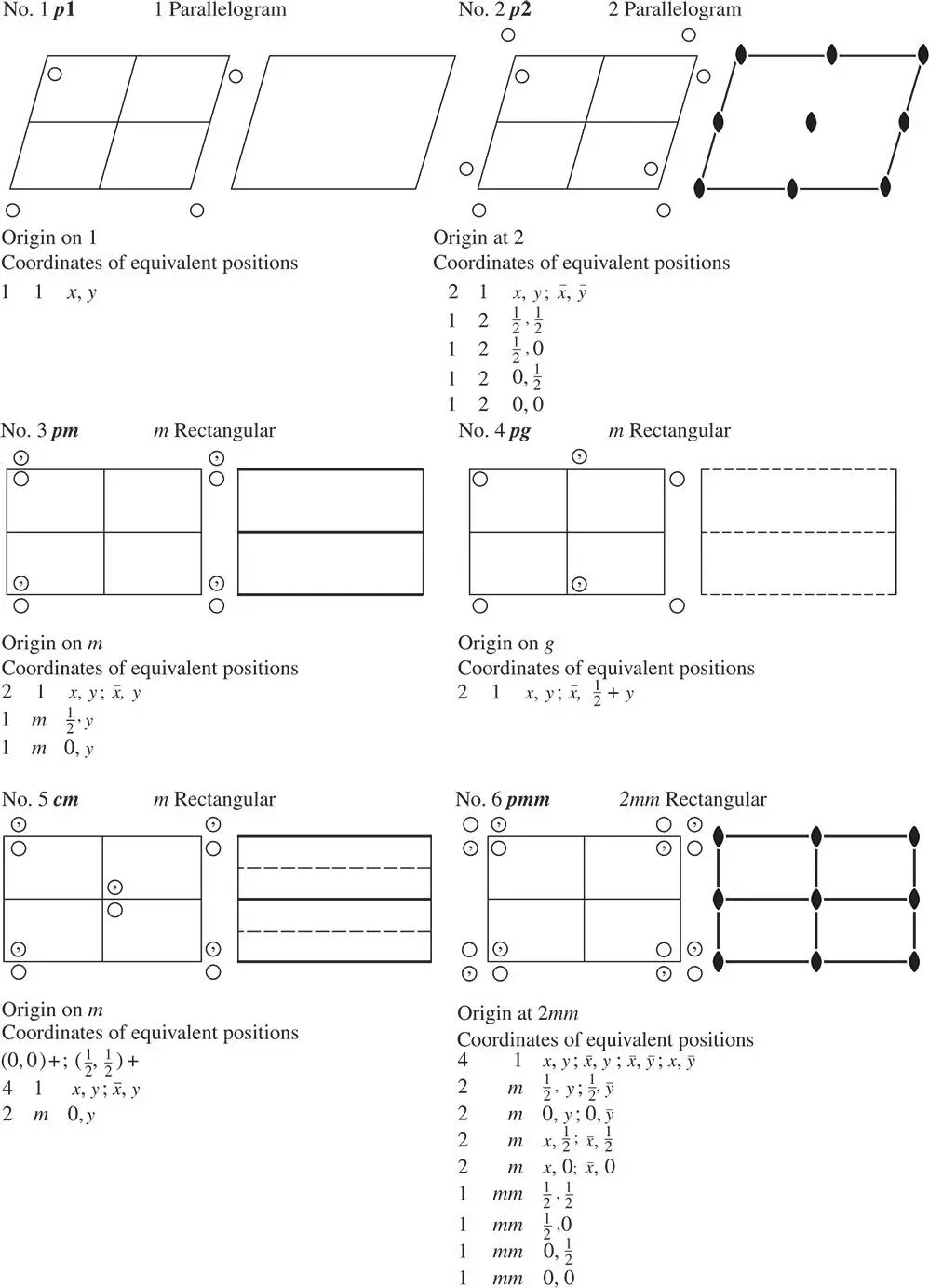
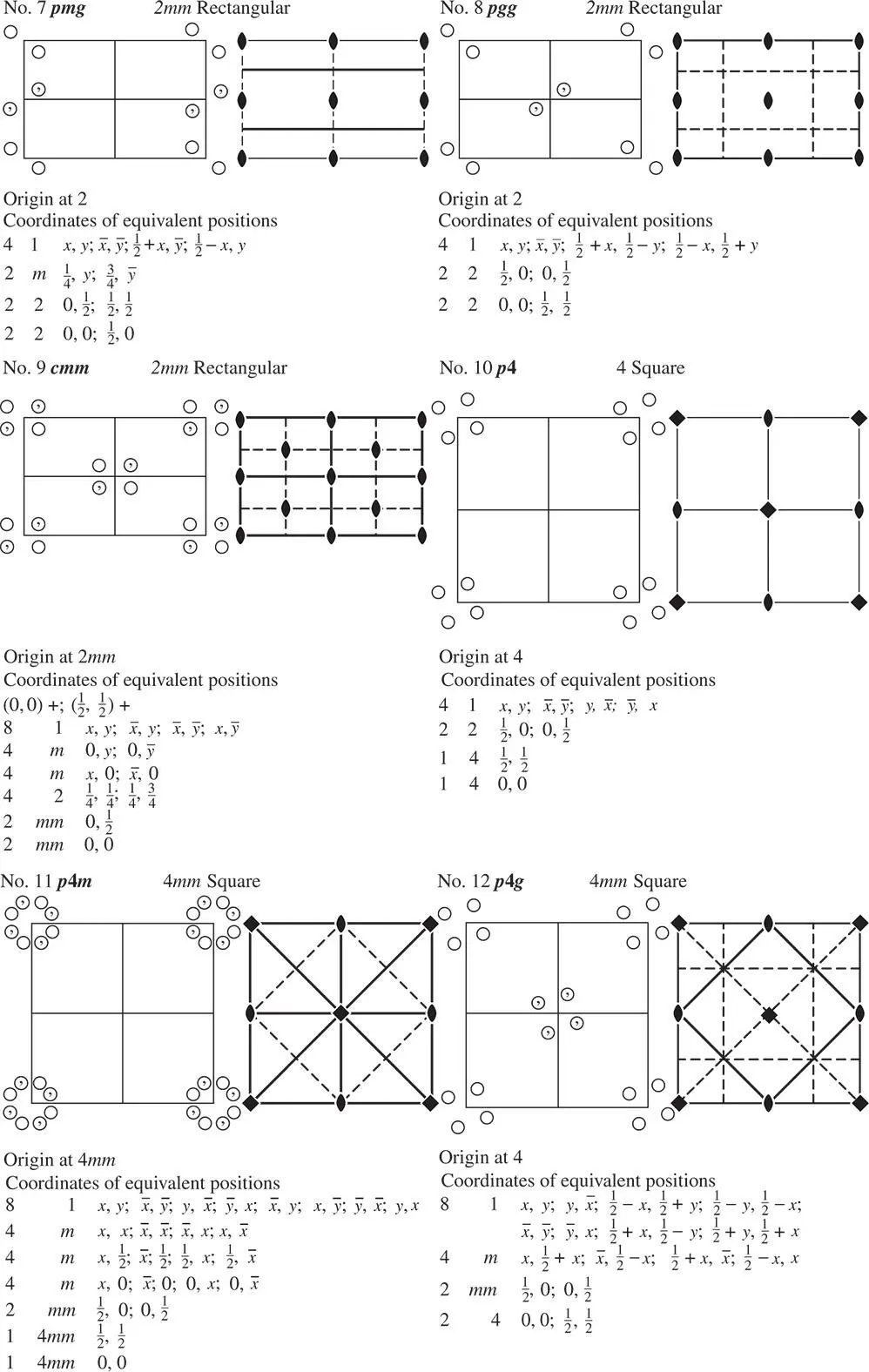
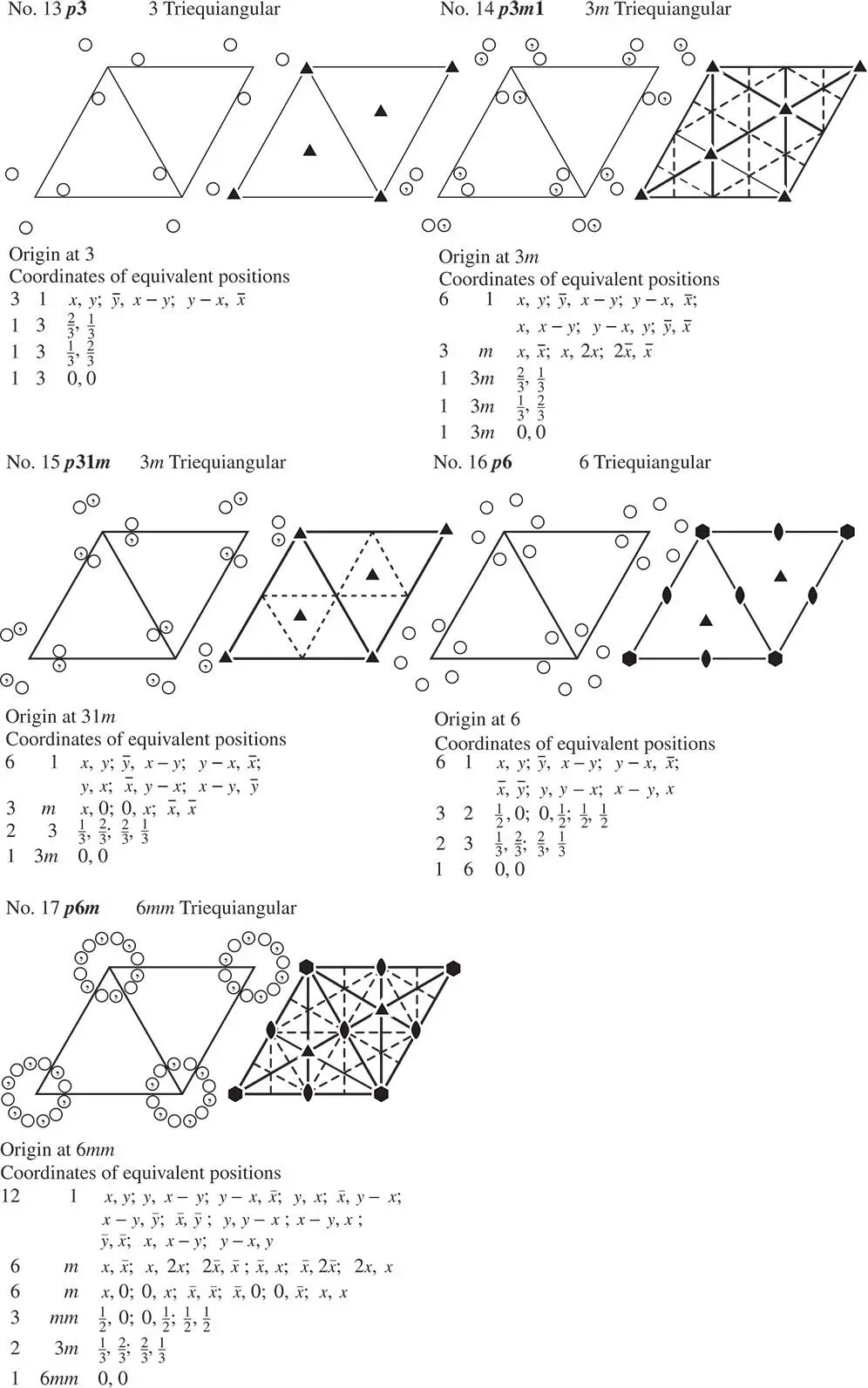
Figure 2.24The 17 two‐dimensional space groups arranged following the International Tables for Crystallography [3]. The headings for each figure read, from left to right, Number, Short Symbol (see Table 2.4), Point Group, Net. Below each figure the columns give the number of equivalent positions, the point group symmetry at those positions and the coordinates of the equivalent positions. The coordinates of positions x and y are expressed in units equal to the cell edge length in these two directions
Space groups are obtained by the application of point group symmetry to finite lattices, the possibility of translation symmetry being taken into account. There are five lattices or nets in two dimensions, shown in Figure 1.14. Following the convention in the International Tables for Crystallography , we shall give them the symbol p for primitive and c for centred. The symbols for twofold, threefold, fourfold and sixfold axes and for the mirror plane are as in Section 2.1. In the most recent editions of the International Tables for Crystallography , the parallelogram net in Figure 1.14a is referred to as an oblique net, and the triequiangular net in Figure 1.14c is referred to as a hexagonal net.
The only additional symmetry element in two dimensions is the glide reflection line: symbol g and denoted by a dashed line in Figure 2.24. It involves reflection and a translation of one‐half of the repeat distance parallel to the line.
The two‐dimensional lattices and the two‐dimensional point groups are combined in Table 2.4to show the space groups that can arise, which are shown in Figure 2.24. In all the diagrams, the x ‐axis runs down the page and the y ‐axis runs across the page, the positive y ‐direction being towards the right. In each of the diagrams the left‐hand one shows the equivalent general positions of the space group; that is, the complete set of positions produced by the operation of the symmetry elements of the space group upon one initial position chosen at random. The total number of general positions is the number falling within the cell, but surrounding positions are also shown to illustrate the symmetry. The right‐hand diagram is that of the group of spatially distributed symmetry operators; that is, the true space (plane) group.
Table 2.4Two‐dimensional lattices, point groups and space groups
| System and lattice symbol |
Point group |
Space group symbols |
Space group number |
| Full |
Short |
| Parallelogram (oblique) p (primitive) |
1 2 |
p 1 p 211 |
p 1 p 2 |
1 2 |
| Rectangular p and c (centred) |
m |
p 1 m 1 p 1 g 1 c 1 m 1 |
pm pg cm |
3 4 5 |
|
2 mm |
p 2 mm p 2 mg p 2 gg c 2 mm |
pmm pmg pgg cmm |
6 7 8 9 |
| Square p |
4 4 mm |
p 4 p 4 mm p 4 gm |
p 4 p 4 m p 4 g |
10 11 12 |
| Triequiangular (hexagonal) p |
3 3 m |
p 3 p 3 m 1 p 31 m |
p 3 p 3 m 1 p 31 m |
13 14 15 |
|
6 6 mm |
p 6 p 6 mm |
p 6 p 6 m |
16 17 |
Note: The two distinct space groups p 3 m 1 and p 31 m correspond to different orientations of the point group relative to the lattice. This does not lead to distinct groups in any other case.
Below each of the diagrams in Figure 2.24, the equivalent general positions and special positions are also indicated. Special positions are positions located on at least one symmetry operator so that repetition of an initial point produces fewer equivalent positions than in the general case. The symmetry at each special position is also given.
The group p 1 is obtained by combining the parallelogram net and a onefold axis of rotational symmetry. There are no special positions in the cell. The group p 2 arises by combining the parallelogram net and a diad. A mirror plane requires the rectangular net ( Section 1.5) and if this net is combined with a single mirror, the space group pm , No. 3, results. Points  and
and  are in mirror relationship to one another. If the mirror in pm is replaced by a glide reflection line, the space group pg results. In No. 4 the glide reflection line g runs normal to the x ‐axis. The centred rectangular lattice necessarily shows a glide reflection line as in cm , No. 5, but only one of these needs to be be present, corresponding to the plane point group m . Since, in this case, the net is multiply primitive, the motif associated with the lattice point at (
are in mirror relationship to one another. If the mirror in pm is replaced by a glide reflection line, the space group pg results. In No. 4 the glide reflection line g runs normal to the x ‐axis. The centred rectangular lattice necessarily shows a glide reflection line as in cm , No. 5, but only one of these needs to be be present, corresponding to the plane point group m . Since, in this case, the net is multiply primitive, the motif associated with the lattice point at ( 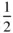 ,
, 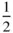 ) is the same as that at (0, 0). Hence the coordinates of equivalent positions, if added to (
) is the same as that at (0, 0). Hence the coordinates of equivalent positions, if added to ( 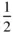 ,
, 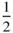 ), give additional equivalent positions.
), give additional equivalent positions.
If two mirror planes at right angles (point group 2 mm ) are combined with the rectangular lattice we get diads at the intersections of the mirrors as in pmm , No. 6. If one or both of the mirrors is replaced by g , the diads no longer lie at the intersections (see pmg , No. 7 and pgg , No. 8). The group cmm , No. 9, necessarily involves the presence of two sets of glide reflection lines, while p 4, No. 10, denotes the square lattice and point group 4, which together necessarily involve the presence of diads. However, mirror planes are not required . If 4 lies at the intersection of two sets of mirrors we have p 4 m , No. 11, the diagonal glide reflection line necessarily being present. However, 4 can also lie at the intersection of two sets of glide reflection lines, in which case again two sets of mirrors arise but the mirrors intersect in diads, giving point group symmetry mm at these points (No. 12). The triequiangular net and point group 3 give the space group p 3 (No. 13). If mirror planes are combined with the triad axis – the combination of the point group 3 m and the triequiangular net – it is found that the mirrors can be arranged in two different ways with respect to the points of the net, yielding p 31 m and p 3 m 1 (Nos. 14 and 15). With the hexagonal point group 6 mm , which necessarily has two sets of mirrors, this duality does not arise and the two space groups are p 6 and p 6 m (Nos. 16 and 17).
Читать дальше




 and
and  are in mirror relationship to one another. If the mirror in pm is replaced by a glide reflection line, the space group pg results. In No. 4 the glide reflection line g runs normal to the x ‐axis. The centred rectangular lattice necessarily shows a glide reflection line as in cm , No. 5, but only one of these needs to be be present, corresponding to the plane point group m . Since, in this case, the net is multiply primitive, the motif associated with the lattice point at (
are in mirror relationship to one another. If the mirror in pm is replaced by a glide reflection line, the space group pg results. In No. 4 the glide reflection line g runs normal to the x ‐axis. The centred rectangular lattice necessarily shows a glide reflection line as in cm , No. 5, but only one of these needs to be be present, corresponding to the plane point group m . Since, in this case, the net is multiply primitive, the motif associated with the lattice point at ( 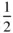 ,
, 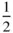 ) is the same as that at (0, 0). Hence the coordinates of equivalent positions, if added to (
) is the same as that at (0, 0). Hence the coordinates of equivalent positions, if added to ( 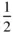 ,
, 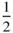 ), give additional equivalent positions.
), give additional equivalent positions.










