2.17 Frequency of Space Groups in Inorganic Crystals and Minerals
Although there are 230 space groups, analyses of the crystal structures of organic compounds and inorganic crystals and minerals show that these structures clearly favour some space groups over others. Thus, for example, almost 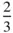 of inorganic crystal structures belong to one of 24 space groups [21]. For organic compounds just two space groups, P 2 1/ c and
of inorganic crystal structures belong to one of 24 space groups [21]. For organic compounds just two space groups, P 2 1/ c and 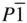 , account for over half the crystal structures solved by 1990 [22], while for monomeric proteins, the space group P 2 12 12 1accounts for almost one third of crystal structures solved by 1995 [23]. Packing and entropic considerations of atoms and molecules, discussed in Chapters 3 and 4, both help to rationalize these observations [21–23]. The consequence of these observations and considerations is that some space groups are markedly less important than others for crystal structure determination [21]. In this context, the choice of Pnma , No. 62, as the three‐dimensional space group to highlight in Section 2.16is deliberate – this space group is the most frequent space group found in inorganic crystals and minerals, accounting for just over 7% of all crystal structures [21], and it is relatively easy to represent in two dimensions in terms of information in the form of diagrams and symmetry data.
, account for over half the crystal structures solved by 1990 [22], while for monomeric proteins, the space group P 2 12 12 1accounts for almost one third of crystal structures solved by 1995 [23]. Packing and entropic considerations of atoms and molecules, discussed in Chapters 3 and 4, both help to rationalize these observations [21–23]. The consequence of these observations and considerations is that some space groups are markedly less important than others for crystal structure determination [21]. In this context, the choice of Pnma , No. 62, as the three‐dimensional space group to highlight in Section 2.16is deliberate – this space group is the most frequent space group found in inorganic crystals and minerals, accounting for just over 7% of all crystal structures [21], and it is relatively easy to represent in two dimensions in terms of information in the form of diagrams and symmetry data.
These point groups and space groups are an extension of the 10 two‐dimensional and 32 three‐dimensional point groups and the 17 two‐dimensional space groups and 230 three‐dimensional space groups. They recognize the effect of an antisymmetry operation on these groups.
Antisymmetry defined by Alan Mackay is ‘the correspondence of faces, points or other crystallographic objects having some property denoted by a positive sign to other faces, points or objects symmetrically related in position, but having the same property denoted with the opposite sign’ [24].
An example of an antisymmetry operation is magnetic spin, so that each atom site can have one of two possible values: spin ‘up’ or spin ‘down’ when the magnetic moments are not randomly arranged, but are instead aligned. A further example is where one atom is coloured one colour, say black, and the other identical atom symmetrically related in position is coloured a different colour, say white.
These groups are known by a variety of names:
magnetic groups,
antisymmetry groups,
Shubnikov groups (after Aleksei Vasilevich Shubnikov, 1887–1970),
Heesch groups (after Heinrich Heesch, 1906–1995, who introduced the concept of antisymmetry in his 1930 paper [25]),
dichromatic groups,
black‐and‐white groups.
Groups where equal and opposite black and white objects are exactly superposed are termed grey groups.
The principle behind the extension of the ‘conventional’ point groups and space groups can be illustrated in two dimensions by considering the five two‐dimensional Bravais lattices ( Figure 1.14). If these five two‐dimensional lattices are centred by (lattice) points of a different colour, the number of permissible Bravais lattices increases from 5 to 10, as shown below in Figure 2.26[24].
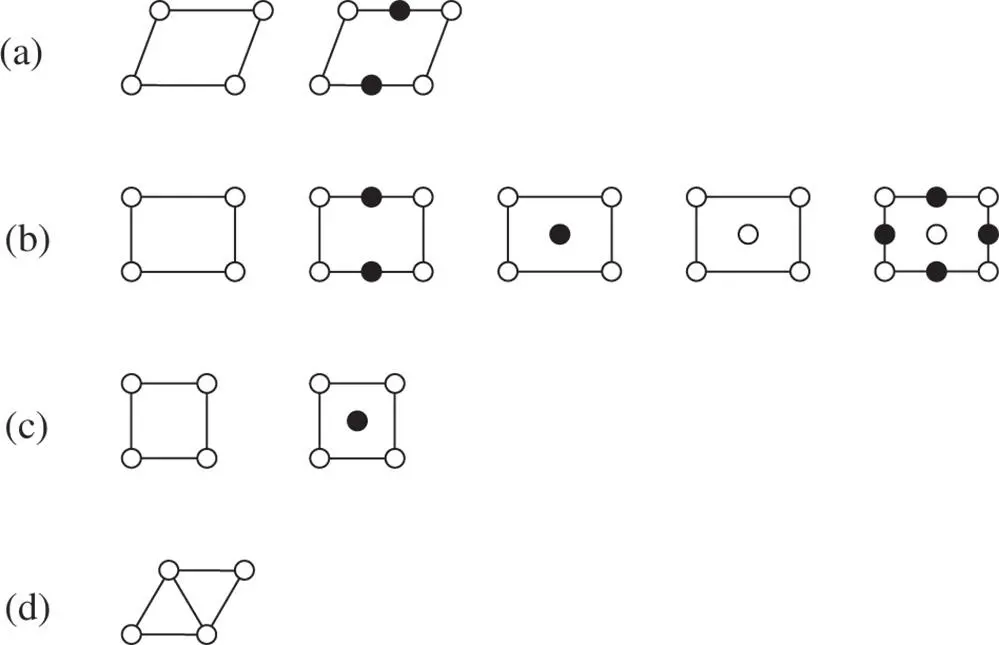
Figure 2.26The 10 black‐and‐white plane lattices: (a) parallelogram (oblique), (b) rectangular, (c) square, (d) equiangular (hexagonal) (after [24])
Here, the five ‘conventional’ two‐dimensional Bravais lattices consistent with translational symmetry have lattice points shown as circles. The five new Bravais lattices which arise from the centring are shown as lattices with the same numbers of circles and dots per unit cell.
In two dimensions there are in total 46 black‐and‐white point groups, to which can be added 17 ‘ordinary’ plane groups and 17 grey groups, giving 80 plane groups in total. In three dimensions there are 1651 Shubnikov space groups: 230 ‘ordinary’ space groups, 230 grey groups, 674 groups where antisymmetry alone generates further groups and 517 where antitranslations and antisymmetry generate further groups [26].
An example of a material where these considerations are relevant is MnO below its Curie temperature of 120 °C. Above 120 °C MnO has the NaCl crystal structure ( Section 3.5.1, Figure 3.16). As is shown in Figure 2.27, the effect of antisymmetry, in this case antiferromagnetic coupling, has the effect of doubling the actual magnetic unit cell relative to the chemical unit cell [27].
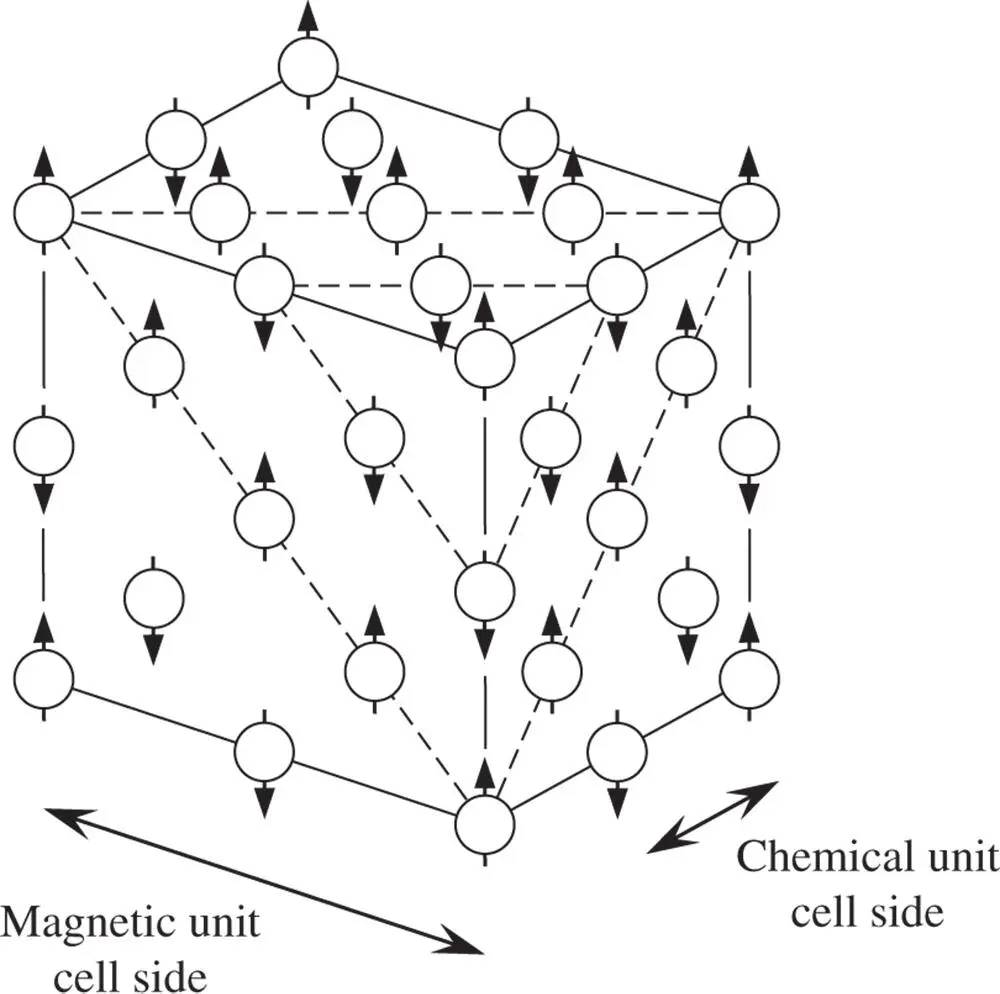
Figure 2.27The effect of antiferromagnetic coupling on the size of the unit cell in MnO. In alternate {111} planes, shown as dotted lines, Mn atoms are either spin ‘up’ or spin ‘down’. As a result, the magnetic unit cell has a cell size twice that of the chemical unit cell. For ease of representation, only Mn atoms are shown in this diagram
An extended introduction to magnetic groups is given in chapter 3.6 of [3]. A complete discussion and descriptions of the magnetic groups is given in the recent book by Litvin [28]. The book by Shubnikov and Kopstik has, in addition, a discussion of coloured symmetry groups – groups relating objects of more than two colours, together with a full set of references to prior work in this area [26].
Material in Appendices 1–3 may be useful; in Problem 2.12 the material in Appendix 4 may also be useful .
1 2.1 Using Figure 2.13, confirm that in the four‐index notation for a plane with indices (hkil):( Eq. (2.2).) Confirm also that the condition for a four‐index vector [UVTW] to lie in a four‐index plane (hkil) is:( Eq. (2.5).)
2 2.2 Show that the angle γ between any of the crystal axes and the unique triad axis in a trigonal crystal is given by:
3 2.3 The corners of a wooden model of a cube are cut off to make equal faces of the form {111}. The first four new faces are cut in positions (111), (11), (11) and (1), in that order. Draw sketch stereograms to show the symmetry elements shown by the model after each new face is formed. What is the crystal system of the model in each case?
4 2.4Sketch stereograms showing the operation of the undermentioned symmetry elements on two distinct poles, each in a general position, and insert the symmetry elements themselves, except the centre of symmetry:centre of symmetryvertical plane of symmetryhorizontal plane of symmetryvertical axes 2, 3, 4, 6vertical inversion axes , , , horizontal axes 2, 4horizontal inversion axis .The symbol is not used in conventional point group notation. Draw sketch stereograms of the poles of one general form for each possible value of X and hence derive the conventional symbols that are actually used.
5 2.5In which of the trigonal classes 3, , 3m, 32, and m does a rhombohedron occur as a special form? In what class is the rhombohedron the general form?Which of the tetragonal classes 4, , 4/m, 422, 4mm, 2m, and 4/mmm have closed forms as their general forms?To which of the cubic classes 23, m, 432, 3m and mm could a crystal belong which had the shape of (i) an octahedron, (ii) a tetrahedron or (iii) an icositetrahedron? (The icositetrahedron is the name given to the {112} form with 24 faces.)
Читать дальше

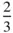 of inorganic crystal structures belong to one of 24 space groups [21]. For organic compounds just two space groups, P 2 1/ c and
of inorganic crystal structures belong to one of 24 space groups [21]. For organic compounds just two space groups, P 2 1/ c and 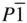 , account for over half the crystal structures solved by 1990 [22], while for monomeric proteins, the space group P 2 12 12 1accounts for almost one third of crystal structures solved by 1995 [23]. Packing and entropic considerations of atoms and molecules, discussed in Chapters 3 and 4, both help to rationalize these observations [21–23]. The consequence of these observations and considerations is that some space groups are markedly less important than others for crystal structure determination [21]. In this context, the choice of Pnma , No. 62, as the three‐dimensional space group to highlight in Section 2.16is deliberate – this space group is the most frequent space group found in inorganic crystals and minerals, accounting for just over 7% of all crystal structures [21], and it is relatively easy to represent in two dimensions in terms of information in the form of diagrams and symmetry data.
, account for over half the crystal structures solved by 1990 [22], while for monomeric proteins, the space group P 2 12 12 1accounts for almost one third of crystal structures solved by 1995 [23]. Packing and entropic considerations of atoms and molecules, discussed in Chapters 3 and 4, both help to rationalize these observations [21–23]. The consequence of these observations and considerations is that some space groups are markedly less important than others for crystal structure determination [21]. In this context, the choice of Pnma , No. 62, as the three‐dimensional space group to highlight in Section 2.16is deliberate – this space group is the most frequent space group found in inorganic crystals and minerals, accounting for just over 7% of all crystal structures [21], and it is relatively easy to represent in two dimensions in terms of information in the form of diagrams and symmetry data.












