Subtle differences in the nomenclature used here for the two‐dimensional space groups and that used in the various editions of the International Tables for Crystallography, such as choosing to describe space group No. 7 as p 2 mg rather than pmg , reflect the fact that for this two‐dimensional space group the presence of a mirror plane at right angle to a glide plane generates the diad. Similarly, in space group No. 17, the presence of one set of mirrors and the sixfold axes generates the second set of mirrors, and so the space group can be described either as p 6 m or p 6 mm ( Table 2.4).
2.14 Nomenclature for Point Groups and Space Groups
The nomenclature we have introduced in this chapter to describe point groups and space groups conforms to a notation known as the Hermann–Mauguin notation arising from the work of Carl Hermann [14] and Charles‐Victor Mauguin [15] and used in the Internationale Tabellen zur Bestimmung von Kristallstrukturen , edited by Hermann and published in 1935. However, another notation for describing point group and space group symmetry is also in common use. This second notation, known as the Schoenflies notation, is named after Arthur Moritz Schoenflies [13]. This latter notation is used in particular in physical chemistry in connection with molecular symmetry and molecular spectroscopy [16], and it is also useful when considering group theoretical aspects of point groups and space groups [17]. The equivalence between the Hermann–Mauguin notation and the Schoenflies notation is discussed in detail by Hans Burzlaff and Helmuth Zimmermann in chapter 3.3 of [3]. The reason why the Hermann–Mauguin notation might be preferred over the Schoenflies notation is neatly summarized by Phillips [2]: ‘ each space group symbol [in the Hermann–Mauguin notation] conveys all the essential information, whereas we must always have a catalogue at hand to follow an arbitrary serial numbering such as that of Schoenflies’ (p. 340).
2.15 Groups, Subgroups, and Supergroups
It is evident from the discussion in this chapter on point groups and space groups that each point group and space group consists of a self‐consistent finite set of symmetry operations. Therefore, point groups and space groups can be described in the formalism of group theory [17–19]. A group G is a set of elements g 1, g 2, g 3… g nwhich conform to the following four conditions [19]:
1 The product gigj of any two group elements must be another element within the group.
2 Group multiplication is associative: (gigj)gk = gi(gjgk).
3 There is a unique group element I called the identity element belonging to G so that its operation on a member of the group g is such that Igi = giI = gi.
4 Each element within the group has a unique inverse; that is, for each gi there is a unique element gi−1 so that gigi−1 = gi−1 gi = I.
Thus, for example, following the example of the point group mmm used by de Jong [5], p. 20, the eight group elements within this point group are: the identity, I ; three 180° rotations about the x ‐, y ‐ and z ‐axes; three reflections in the (100), (010) and (001) planes; and a centre of symmetry. A subgroup of these symmetry elements is found in 2 mm : the identity, a 180° rotation about the x ‐axis and two reflections in the (010) and (001) planes. Other subgroups are the point groups 222, 2/ m , m , 2,  , and 1. Conversely, the point group mmm is clearly a supergroup for 2 mm and 222.
, and 1. Conversely, the point group mmm is clearly a supergroup for 2 mm and 222.
Similar principles apply to subgroups and supergroups of space groups. Thus, for example, following Hans Wondratschek in chapter 8 in Volume A of the revised, fifth edition of the International Tables for Crystallography [20], the space group P 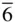 2 m is one member of the group whose minimal nonisomorphic supergroup is P 6 3/ mcm ; it has as maximal nonisomorphous subgroups P
2 m is one member of the group whose minimal nonisomorphic supergroup is P 6 3/ mcm ; it has as maximal nonisomorphous subgroups P 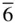 , P 321, P 31 m and Pm 2 m . (Groups are termed isomorphic if they have an equivalent group multiplication structure, but differ in the nature of the elements constituting them [19]. Thus, for example, the point groups 2/ m , 222 and 2 mm are isomorphic: all three have four elements within the group and the same multiplication structure within them.)
, P 321, P 31 m and Pm 2 m . (Groups are termed isomorphic if they have an equivalent group multiplication structure, but differ in the nature of the elements constituting them [19]. Thus, for example, the point groups 2/ m , 222 and 2 mm are isomorphic: all three have four elements within the group and the same multiplication structure within them.)
2.16 An Example of a Three‐Dimensional Space Group
To illustrate the principles we have outlined in Sections 2.12– 2.14, an example of an entry from in Volume A of the revised, fifth edition of the International Tables for Crystallography [20] is shown in Figure 2.25. In the more recent sixth, revised edition of these Tables , the data tabulated in the revised, fifth edition on subgroups and supergroups of the two‐ and three‐dimensional space groups and shown in Figure 2.25has been moved to Volume A1.
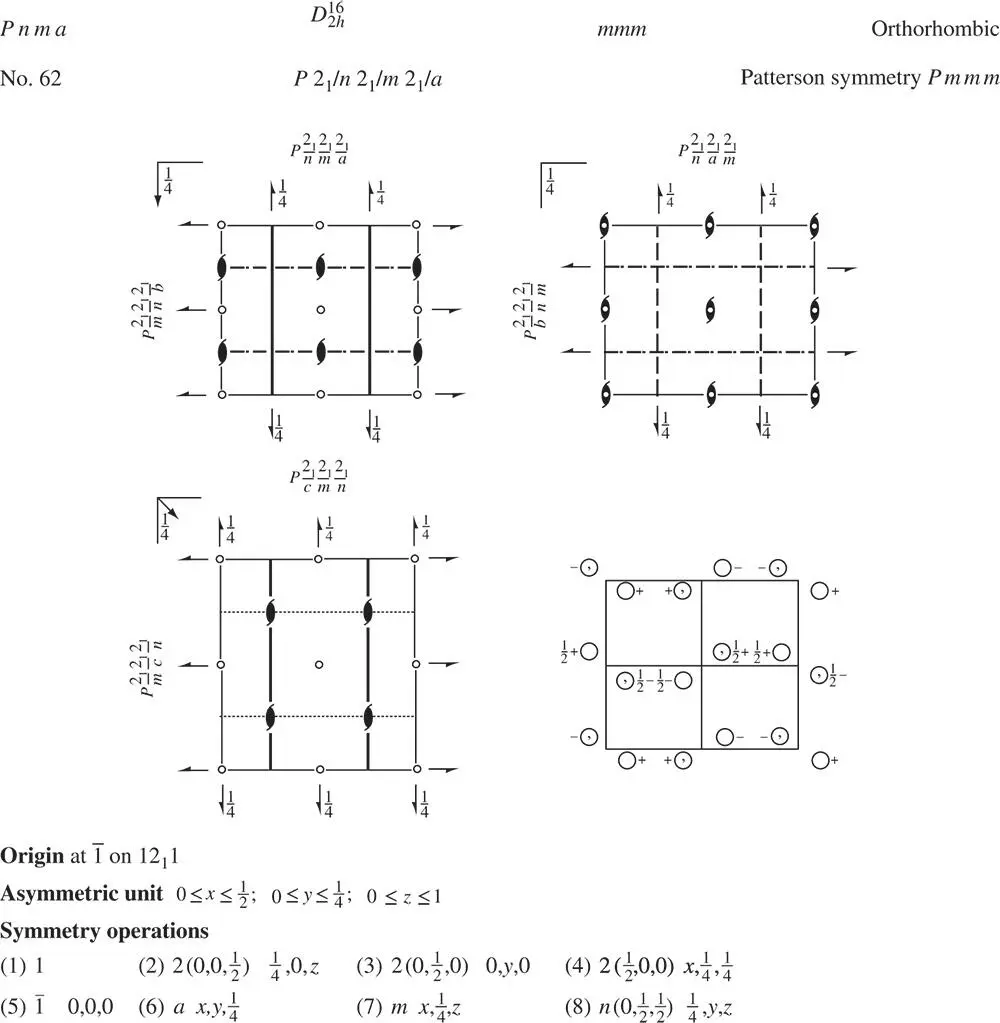
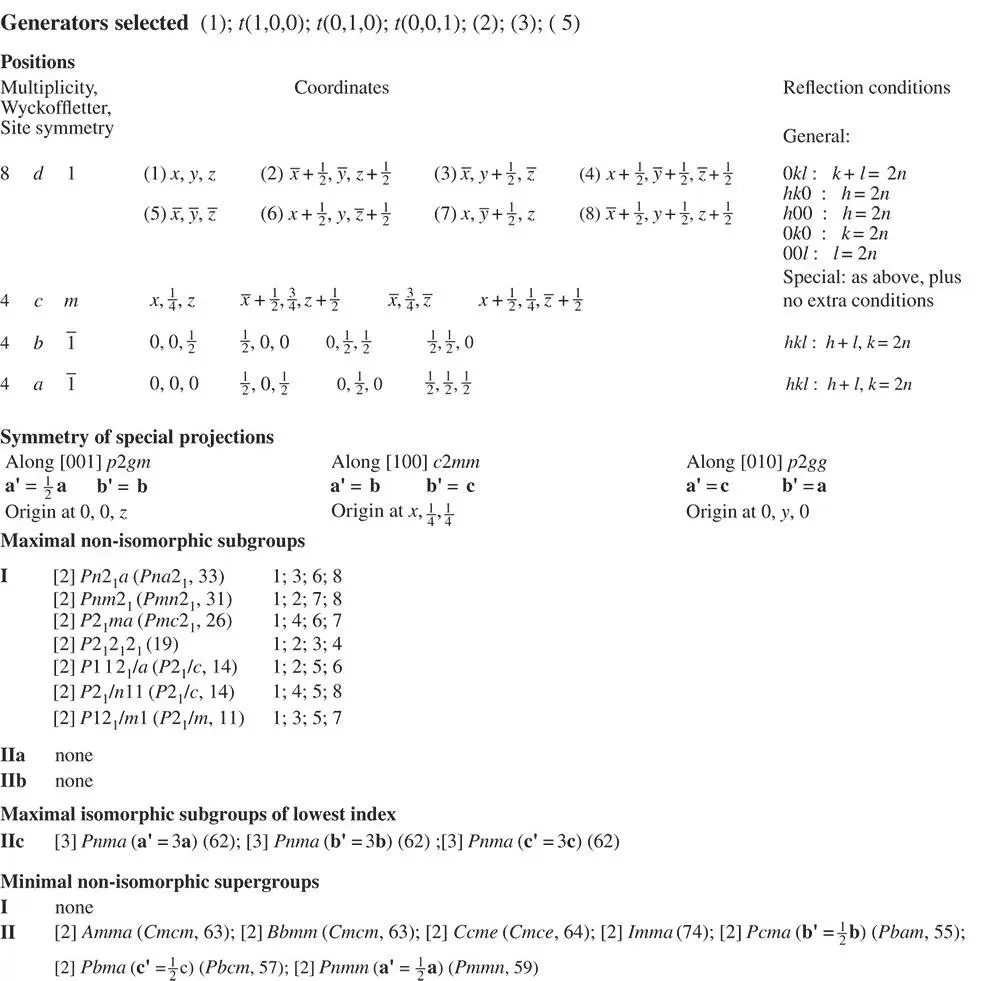
Figure 2.25An example of a space group.
Source: Taken from [20].
It is apparent from the Hermann–Mauguin notation of this space group, Pnma , No. 62, that crystals with this space group symmetry belong to the orthorhombic crystal system, point group mmm . The Schoenflies notation 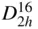 indicates that the space group is dihedral (or two‐sided; from the ‘ D ’), that it has a twofold rotation axis (from the ‘2’), that there is in addition a mirror plane perpendicular to this twofold axis (from the ‘ h ’ subscript) and that it is the 16th of 28 such space groups
indicates that the space group is dihedral (or two‐sided; from the ‘ D ’), that it has a twofold rotation axis (from the ‘2’), that there is in addition a mirror plane perpendicular to this twofold axis (from the ‘ h ’ subscript) and that it is the 16th of 28 such space groups 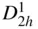 …
… 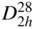 (space groups 47–74 inclusive), all of which are space groups derived from the mmm point group.
(space groups 47–74 inclusive), all of which are space groups derived from the mmm point group.
The full Hermann–Mauguin notation for this space group is P 2 1/ n 2 1/ m 2 1/ a , showing that there are three mutually perpendicular sets of screw diads in addition to the mirror, m , and the diagonal, n , and axial, a , glide planes. The diagrams of the symmetry elements of the group follow the principles in Figure 2.24, with the use of standard graphical symbols for n (parallel to (100)) and a (parallel to (001)). The projections in the top left‐hand corner and the bottom right‐hand corner are both down [001], the one in the top right‐hand corner down [010] and the one in the bottom left‐hand corner down [100].
The asymmetric unit is ‘a (simply) connected smallest part of space from which, by application of all symmetry operations of the space group, the whole of space is filled exactly’ [20]. The listing under the heading ‘Symmetry Operations’ in Figure 2.25is a summary of the various geometric descriptions of each of the eight symmetry operations in the space group, numbered (1)–(8). Thus, for example, here the second of these, 2 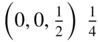 , 0, z , defines the screw diad parallel to [001] intersecting the x – y plane at (
, 0, z , defines the screw diad parallel to [001] intersecting the x – y plane at ( 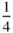 , 0). The ‘Generators Selected' define the order in which the coordinates of the symmetrically equivalent positions are produced; for example, the coordinates related by symmetry to the general position x , y , z in the space group. (1) is the identity operation, showing that in this case integral lattice translations produce the equivalent point in adjacent unit cells. After the ‘Positions', which follow the protocol described in Section 2.12, and the ‘Symmetry of Special Projections', which are self‐explanatory, a summary is given of subgroups and supergroups related to the space group under consideration, following the methodology set out in chapter 2 of [20]. Finally, the reflection conditions listed under ‘Positions’ specify the systematic absences which occur under kinematical diffraction conditions, such as X‐ray diffraction.
, 0). The ‘Generators Selected' define the order in which the coordinates of the symmetrically equivalent positions are produced; for example, the coordinates related by symmetry to the general position x , y , z in the space group. (1) is the identity operation, showing that in this case integral lattice translations produce the equivalent point in adjacent unit cells. After the ‘Positions', which follow the protocol described in Section 2.12, and the ‘Symmetry of Special Projections', which are self‐explanatory, a summary is given of subgroups and supergroups related to the space group under consideration, following the methodology set out in chapter 2 of [20]. Finally, the reflection conditions listed under ‘Positions’ specify the systematic absences which occur under kinematical diffraction conditions, such as X‐ray diffraction.
Читать дальше

 , and 1. Conversely, the point group mmm is clearly a supergroup for 2 mm and 222.
, and 1. Conversely, the point group mmm is clearly a supergroup for 2 mm and 222.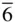 2 m is one member of the group whose minimal nonisomorphic supergroup is P 6 3/ mcm ; it has as maximal nonisomorphous subgroups P
2 m is one member of the group whose minimal nonisomorphic supergroup is P 6 3/ mcm ; it has as maximal nonisomorphous subgroups P 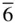 , P 321, P 31 m and Pm 2 m . (Groups are termed isomorphic if they have an equivalent group multiplication structure, but differ in the nature of the elements constituting them [19]. Thus, for example, the point groups 2/ m , 222 and 2 mm are isomorphic: all three have four elements within the group and the same multiplication structure within them.)
, P 321, P 31 m and Pm 2 m . (Groups are termed isomorphic if they have an equivalent group multiplication structure, but differ in the nature of the elements constituting them [19]. Thus, for example, the point groups 2/ m , 222 and 2 mm are isomorphic: all three have four elements within the group and the same multiplication structure within them.)

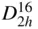 indicates that the space group is dihedral (or two‐sided; from the ‘ D ’), that it has a twofold rotation axis (from the ‘2’), that there is in addition a mirror plane perpendicular to this twofold axis (from the ‘ h ’ subscript) and that it is the 16th of 28 such space groups
indicates that the space group is dihedral (or two‐sided; from the ‘ D ’), that it has a twofold rotation axis (from the ‘2’), that there is in addition a mirror plane perpendicular to this twofold axis (from the ‘ h ’ subscript) and that it is the 16th of 28 such space groups 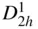 …
… 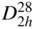 (space groups 47–74 inclusive), all of which are space groups derived from the mmm point group.
(space groups 47–74 inclusive), all of which are space groups derived from the mmm point group.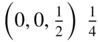 , 0, z , defines the screw diad parallel to [001] intersecting the x – y plane at (
, 0, z , defines the screw diad parallel to [001] intersecting the x – y plane at ( 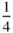 , 0). The ‘Generators Selected' define the order in which the coordinates of the symmetrically equivalent positions are produced; for example, the coordinates related by symmetry to the general position x , y , z in the space group. (1) is the identity operation, showing that in this case integral lattice translations produce the equivalent point in adjacent unit cells. After the ‘Positions', which follow the protocol described in Section 2.12, and the ‘Symmetry of Special Projections', which are self‐explanatory, a summary is given of subgroups and supergroups related to the space group under consideration, following the methodology set out in chapter 2 of [20]. Finally, the reflection conditions listed under ‘Positions’ specify the systematic absences which occur under kinematical diffraction conditions, such as X‐ray diffraction.
, 0). The ‘Generators Selected' define the order in which the coordinates of the symmetrically equivalent positions are produced; for example, the coordinates related by symmetry to the general position x , y , z in the space group. (1) is the identity operation, showing that in this case integral lattice translations produce the equivalent point in adjacent unit cells. After the ‘Positions', which follow the protocol described in Section 2.12, and the ‘Symmetry of Special Projections', which are self‐explanatory, a summary is given of subgroups and supergroups related to the space group under consideration, following the methodology set out in chapter 2 of [20]. Finally, the reflection conditions listed under ‘Positions’ specify the systematic absences which occur under kinematical diffraction conditions, such as X‐ray diffraction.










