Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers
Здесь есть возможность читать онлайн «Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Fundamentals of Numerical Mathematics for Physicists and Engineers
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Fundamentals of Numerical Mathematics for Physicists and Engineers: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Fundamentals of Numerical Mathematics for Physicists and Engineers»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Fundamentals of Numerical Mathematics for Physicists and
Engineers
Provides a modern perspective of numerical mathematics by introducing top-notch techniques currently used by numerical analysts Contains two parts, each of which has been designed as a one-semester course Includes computational practicals in Matlab (with solutions) at the end of each section for the instructor to monitor the student's progress through potential exams or short projects Contains problem and exercise sets (also with solutions) at the end of each section is an excellent book for advanced undergraduate or graduate students in physics, mathematics, or engineering. It will also benefit students in other scientific fields in which numerical methods may be required such as chemistry or biology.

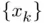 is said to be converged to the desired tolerance
is said to be converged to the desired tolerance 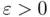 after
after 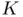 iterations if
iterations if  ,
, 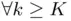 .
.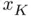 , it is always advisable to check the magnitude of
, it is always advisable to check the magnitude of  in order to confirm if the method has succeeded. The code below is a simple implementation of the bisection method using the tolerance criterion previously described:
in order to confirm if the method has succeeded. The code below is a simple implementation of the bisection method using the tolerance criterion previously described: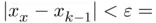
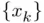 seems to be a Cauchy Sequence 6 (that is,
seems to be a Cauchy Sequence 6 (that is, 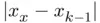 decreases with increasing
decreases with increasing 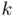 ), its convergence is guaranteed. While a convergent sequence must necessarily be of Cauchy type, the reverse statement is, in general, not true (although here it will be assumed to be). Second, the quantity
), its convergence is guaranteed. While a convergent sequence must necessarily be of Cauchy type, the reverse statement is, in general, not true (although here it will be assumed to be). Second, the quantity 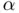 has disappeared from the convergence criteria. In other words, once
has disappeared from the convergence criteria. In other words, once 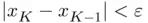 for some
for some 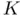 and beyond, we only know that the sequence has converged (in the practical sense) to some value
and beyond, we only know that the sequence has converged (in the practical sense) to some value 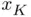 , that henceforth will play the role of the numerical root within the prescribed tolerance.
, that henceforth will play the role of the numerical root within the prescribed tolerance.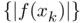 , usually called the residuals . Since this quantity should approach zero when
, usually called the residuals . Since this quantity should approach zero when 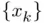 converges to a root, the reader may wonder why
converges to a root, the reader may wonder why 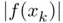 should not be used as a measure for stopping the iterations. The reason is that the residual is not always a reliable measure (although it is often used in practice to decide convergence). We will address this question later in this chapter, when we introduce the concept of condition number of a root .
should not be used as a measure for stopping the iterations. The reason is that the residual is not always a reliable measure (although it is often used in practice to decide convergence). We will address this question later in this chapter, when we introduce the concept of condition number of a root .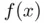 is differentiable and that the root is close to some initial guess
is differentiable and that the root is close to some initial guess 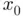 . To get a better estimation of the root we assume that, close to
. To get a better estimation of the root we assume that, close to 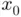 , the function
, the function 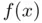 can be approximated by its tangent line
can be approximated by its tangent line 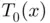 at the point
at the point  plotted in gray below. In other words, we locally approximate
plotted in gray below. In other words, we locally approximate 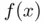 by its first order Taylor expansion
by its first order Taylor expansion 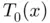 at
at 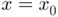 :
: