Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

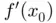where is the value of the derivative of 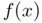at 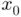. The motivation for approximating 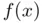by 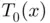is simple: if 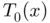is a reasonably good approximation of 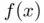, then the solution of should be a reasonable good estimation of the solution of 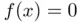. Let 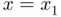be the solution of 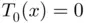satisfying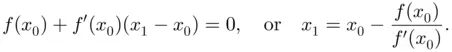

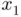(1.7)

The resulting abscissa where 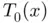intercepts the 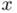‐axis is the new (hopefully more accurate) estimation of the root. The process can be repeated approximating 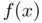by its Taylor expansion 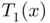at 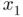(straight gray line below the curve) in order to obtain an even better estimation 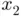satisfying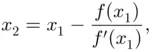

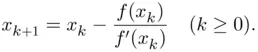
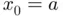(1.8)

and so on, leading to the iterative formula:

Newton's Iteration:

(1.9)

A simple implementation of Newton's method can be found in the next code, whose structure essentially differs from the one seen in the bisection in two main aspects. First, the code needs an initial guess as starting point, instead of an interval. Second, in addition to the string name corresponding to the M‐file function 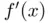fun, the code also needs the one associated with in the argument 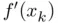dfun. Providing the M‐file for the exact derivative entails both analytical differentiation and its subsequent programming, both being error‐prone tasks. While this is the correct procedure, it is sometimes advisable to let the computer do the job by approximating the value of by the ratio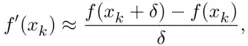

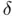(1.10)

where is a small increment ( 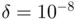in our code). This approximation of the derivative, along with the suitability of the chosen 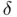, will be properly justified later in the chapter devoted to numerical differentiation. 9 The reader may check that there are no noticeable differences when using either the exact or the approximate derivative ( 1.10).

% Code 2: Newton's method for solving f(x) = 0 % Input: 1. a: initial guess % 2. tol: tolerance so that abs(x_k+1 - x_k) < tol % 3. itmax: maximum number of iterations allowed % 4. fun: function's name % 5. dfun: derivative's name % (If dfun = ‘0’, then f'(x) is approximated) % Output: 1. xk: resulting sequence % 2. res: resulting residuals % 3. it: number of required iterations function [xk,res,it] = newton(a,tol,itmax,fun,dfun) xk = [a]; fk = feval(fun,xk); res = abs(fk); it = 0; tolk = res(1); dx = 1e-8 ; while it < itmax & tolk > tol if dfun == ‘0’ dfk = (feval(fun,xk(end)+dx)-fk)/dx; else dfk = feval(dfun,xk(end)); end xk = [xk, xk(end) - fk/dfk]; fk = feval(fun,xk(end)); res = [res abs(fk)]; tolk = abs(xk(end)-xk(end-1)); it = it + 1; end

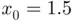Let us compare the performance of Newton's method with the bisection by applying both algorithms to solve the cubic equation ( 1.2) starting from the same initial guess . The first two columns of Table 1.1outline the sequences 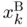and 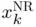resulting from the bisection and Newton–Raphson methods, respectively. While the bisection method requires almost 50 iterations to achieve full accuracy, Newton's method does the same job in just 5. In fact, Newton–Raphson's sequence nearly doubles the number of converged digits from one iterate to the next, whereas in the bisection sequence this number grows very slowly (and sometimes even decreases, as seen from 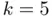to 6). This is better understood when looking at the third and fourth columns of Table 1.1, where we have included the absolute error corresponding to both methods 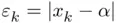, where 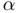is the reference value given in the exact expression ( 1.3), and whose numerical evaluation with Matlab is .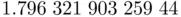