Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

We can rigorously prove the quadratic convergence of Newton's method by evaluating the limit ( 1.11) for

(1.15)

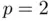
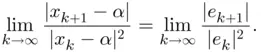
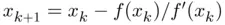Before calculating the limit above, first notice that Newton's iteration can be expressed in terms of the errors 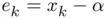. Since 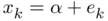we may write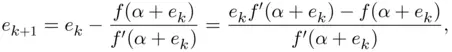

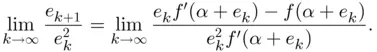
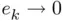and therefore

Since when 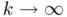, we may define 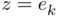as a continuous variable that approaches zero so that we can rewrite the previous limit as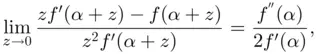

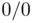where we have used L'Hôpital's rule to solve the indeterminate form . Therefore we conclude that Newton's method has quadratic convergence with asymptotic error constant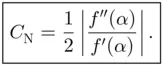

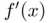(1.16)

One of the drawbacks of Newton's method is that we must supply the derivative of the function at every iteration. As mentioned before, the derivative can be approximated using ( 1.10) so there is no need for providing a supplementary function for the evaluation . Either in the exact or approximate version of Newton's method, we need two function evaluations per iteration. There are situations where two or more evaluations per iteration may be computationally expensive, such as in the case of extending Newton's method to solve systems of nonlinear equations, as we will address in Part II. Now, let us assume that we have to provide a Newton‐like iteration without explicitly appealing to the derivative of 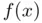and with just one evaluation of 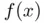per iteration.

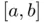Assume that we have identified an interval such that 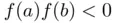. The key point is to provide an estimation 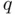of the slope 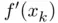of the function at the 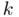th iterate and substitute Newton's iteration by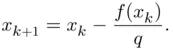

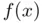(1.17)

Provided that does not oscillate very much within 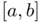, a reasonable estimation of 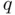is the slope 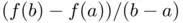provided by the mean value theorem. In this case, the expression ( 1.17) leads to what is usually termed as the chord method :

Chord Iteration:

(1.18)

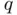The chord method can be improved by updating at every iteration with a new quantity 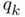obtained from the values of the 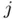th iterates 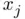and their images 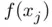obtained at the previous stages 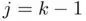and 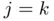: