Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers
Здесь есть возможность читать онлайн «Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Fundamentals of Numerical Mathematics for Physicists and Engineers
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Fundamentals of Numerical Mathematics for Physicists and Engineers: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Fundamentals of Numerical Mathematics for Physicists and Engineers»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Fundamentals of Numerical Mathematics for Physicists and
Engineers
Provides a modern perspective of numerical mathematics by introducing top-notch techniques currently used by numerical analysts Contains two parts, each of which has been designed as a one-semester course Includes computational practicals in Matlab (with solutions) at the end of each section for the instructor to monitor the student's progress through potential exams or short projects Contains problem and exercise sets (also with solutions) at the end of each section is an excellent book for advanced undergraduate or graduate students in physics, mathematics, or engineering. It will also benefit students in other scientific fields in which numerical methods may be required such as chemistry or biology.

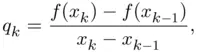
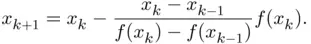
 by taking the initial values
by taking the initial values 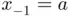 and
and 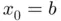 , so that the first iterate
, so that the first iterate 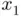 is the same as the one obtained with the chord method. It should be clear that both chord and secant methods involve just the new evaluation
is the same as the one obtained with the chord method. It should be clear that both chord and secant methods involve just the new evaluation 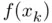 per iteration, the remaining terms being previously computed (and stored) in the past.
per iteration, the remaining terms being previously computed (and stored) in the past.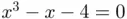 starting from the same initial interval
starting from the same initial interval 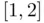 , as was done with Newton's and bisection methods. Figure 1.2b shows the resulting convergence history of the two methods. From the two sets of data of Figure 1.2b we may conclude that while the chord method seems to converge linearly, the secant methods converges superlinearly with an approximate order
, as was done with Newton's and bisection methods. Figure 1.2b shows the resulting convergence history of the two methods. From the two sets of data of Figure 1.2b we may conclude that while the chord method seems to converge linearly, the secant methods converges superlinearly with an approximate order 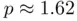 . It can be formally proved that the exact convergence order of the chord method is
. It can be formally proved that the exact convergence order of the chord method is 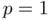 , whereas for the secant method the order is the golden ratio
, whereas for the secant method the order is the golden ratio 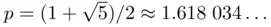 (see exercises at the end of the chapter).
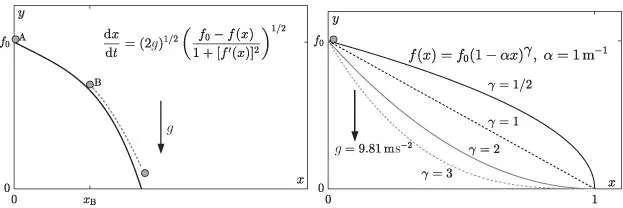
(see exercises at the end of the chapter). initially at rest is released from the highest point of the surface A of height
initially at rest is released from the highest point of the surface A of height 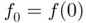 , as shown in the following figure. The object slowly starts to slide under the effects of gravity until it reaches point B at which it loses contact with the surface. The goal of this practical is to determine the abscissa
, as shown in the following figure. The object slowly starts to slide under the effects of gravity until it reaches point B at which it loses contact with the surface. The goal of this practical is to determine the abscissa 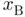 of that point.
of that point.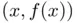 , i.e. still in contact with the surface, is
, i.e. still in contact with the surface, is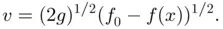
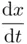 is given by the expression in the figure on the left. Imposing that there is no horizontal acceleration at point B (i.e.
is given by the expression in the figure on the left. Imposing that there is no horizontal acceleration at point B (i.e. 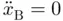 ) show that (excluding points where
) show that (excluding points where 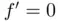 )
)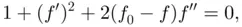
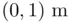 , find the abscissas
, find the abscissas 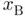 for
for 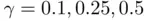 , and 0.9.
, and 0.9.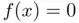 usually involve parameters and constants coming from known external data. For example, Eq. ( 1.5) for the quantum energy levels depend on the well's depth
usually involve parameters and constants coming from known external data. For example, Eq. ( 1.5) for the quantum energy levels depend on the well's depth 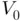 and width
and width 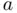 , as well as on the mass of the particle
, as well as on the mass of the particle 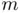 . Therefore, it is obvious that changing the value of
. Therefore, it is obvious that changing the value of 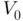 ,
, 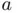 , or
, or 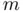 in ( 1.5) will change the value of the corresponding energy levels
in ( 1.5) will change the value of the corresponding energy levels 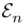 . In particular, we may also expect that if the parameters are changed just by a tiny amount, then the changes in the solutions should also be very small.
. In particular, we may also expect that if the parameters are changed just by a tiny amount, then the changes in the solutions should also be very small.










