For an authoritative study of different root‐finding methods for nonlinear scalar equations, I strongly recommend Dahlquist and Björk's Numerical Methods in Scientific Computing , Vol. I. The reader will find there detailed mathematical proofs of the convergence of many algorithms, as well as other very important topics that have not been covered in this chapter, such as Fixed‐Point Iteration , Minimization or the solution of algebraic equations and deflation . That chapter also addresses the Termination Criteria problem (i.e. when to stop the iteration) in depth and with mathematical rigor.
For a different approach to the root‐finding problem, Acton's Numerical Methods that Work is an alternative. The reader will find in that text very clear geometrical explanations of why different root‐finding methods may have convergence problems. Acton's book also provides deep insight into the technical aspects of root‐finding algorithms, as well as very useful tips and strategies.
Practical 1.2 Throwing Balls and Conditioning
A ball is thrown from the lowest point of a hill 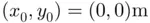 with initial angle
with initial angle 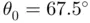 and speed
and speed 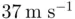 (see the figure below). The height of the hill is given by the expression
(see the figure below). The height of the hill is given by the expression 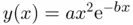 , where
, where 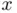 and
and 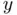 are measured in meters,
are measured in meters, 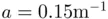 , and
, and 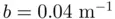 .
.
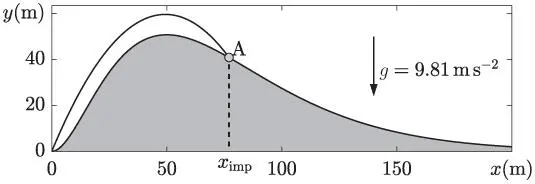
1 Edit a Matlab .m function corresponding to the equation whose solution is the abscissa where the parabola and the hill's profile intersect (for arbitrary initial speed and angle and , respectively).
2 Using Newton's method, find the abscissa of the point A where the ball impacts with the hill. Provide your result with at least five exact figures.
3 With the same initial speed, represent the impact abscissa for initial angles within the range .
4 Find the minimum initial angle that allows the ball to impact beyond , i.e. to the right of the hill's peak. Provide your result with at least three exact figures.
5 Explore the order of convergence of the root‐finding method when computing the minimum angle in (d). Do you observe an increase in the number of iterations required to achieve the desired accuracy? If so, explain what may be the reason for that phenomenon.
The symbol (A) means that the problem has to be solved analytically, whereas (N) means to use numerical Matlab codes. Problems with the symbol * are slightly more difficult.
1 1. (A) Consider the bisection method starting from the interval . Let be the resulting bisection sequence satisfying . Let be a given tolerance.How many iterations are required in order to satisfy that ?Once that tolerance has been reached, how many iterations should be added to have one more digit of precision?
2 2. (N) Apply the bisection algorithm to solve the equations over the intervals indicated below. Provide the numerical approximation of the root with at least 10 significant digits and also report how many bisections were required to achieve that accuracy., ., ., .
3 3. (A) Show that the chord method starting within the interval with has linear convergence to the root and obtain its corresponding asymptotic error constant . If for linear convergence, what constraints does this condition impose? Will the method converge linearly to a double root?
4 4. (A)* Show that the secant method converges superlinearly with order of convergence . As a hint, use Taylor's expansion to show that the errors obey (to the lowest order) the recurrence: .Next, assume that the absolute error obeys the relation , with in order to provide the value of the exponent as well as the asymptotic error constant .
5 5. (N) Using your own codes for the chord and secant methods, solve the equation starting from the interval and reproduce the results of Figure 1.2b.
6 6. (N) Regula Falsi or false position method: this root‐finding algorithm is in essence a globally convergent version of the secant method. Starting from the interval satisfying , proceed with the iterationwhere is the last iterate satisfying , that is,You need to modify your secant method code by storing the history of the iterates in order to include the condition above.Solve again the cubic starting from the interval and compute its local order of convergence based on the sequence obtained. What order can you identify?Solve (see Figure 1.4b) starting from initial intervals containing either or and convince yourself that the method is globally convergent within those intervals. In particular, verify for a few values of that .
7 7. (A) Applying Newton's method to a certain equation leads to the iteration , with . Find the original equation or, equivalently, find the purpose of such iteration and its corresponding limit .
8 8. (A) We apply Newton's method to solve starting from . How many iterations are required to obtain the root with an error of ? Solve the problem analytically. After that, verify your estimation numerically.
9 9. (A) For , find the value of the quantity Hint: is the limit of the sequence
10 10. (A–N) One technique to accelerate Newton's method for roots of multiplicity consists of replacing the original equation by the auxiliary one , where .If is a root of with multiplicity , find the limit .If the modified Newton's iteration using the auxiliary equation reads , find .If we use the original Newton's method to solve starting from , find the minimum number of iterations such that .Repeat (c) using the auxiliary equation.
11 11. (A–N) Steffensen's root‐finding method is given by the iterationStarting from the initial guess , apply the method to solve . What order of convergence can you identify?Solve starting also from . Do you observe the same exponent as in part (a)?(*) Find the exact order of convergence of the method for simple roots, as well as its corresponding asymptotic constant.
12 12. (A–N) Halley's 13 root‐finding method is an algorithm that improves Newton's quadratic convergence when solving . In this case, the method solves the auxiliary equation , where and is assumed to be positive and differentiable within the domain containing the root.Find the resulting iterative formula in terms of , , and .Find the root of within using Halley's method starting from . Can you identify the order of convergence ?
Читать дальше

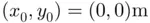 with initial angle
with initial angle 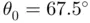 and speed
and speed 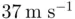 (see the figure below). The height of the hill is given by the expression
(see the figure below). The height of the hill is given by the expression 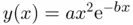 , where
, where 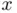 and
and 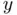 are measured in meters,
are measured in meters, 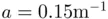 , and
, and 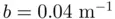 .
.











