Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

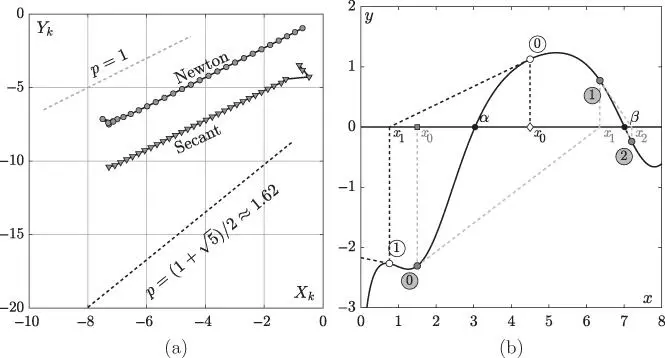
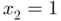Figure 1.4(a) Convergence history of Newton's and secant methods when the sequences approach the double root of equation 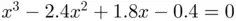. The 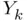ordinates corresponding to the secant method (triangles) have been shifted downwards three units to avoid overlap between the two sets of data and help visualize. (b) Newton's method iterates for the solution of .

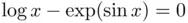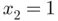Figure 1.4a shows the result of applying Newton's and secant methods to find the double ill‐conditioned root of the equation 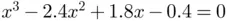studied in Section 1.6. Newton's iteration is started from 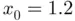, whereas the secant has been initialized from the interval that contains the root. The reader may check that in this case Newton's and secant methods lose their quadratic and golden ratio orders, respectively, both exhibiting linear convergence, as shown in Figure 1.4a. Double or ill‐conditioned roots appear in physics more frequently than one may expect, particularly in problems where the transcendental equation to be solved is the result of imposing some kind of critical or threshold condition (we refer the reader to Practical 1.2, for example).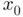

In general, root‐finding methods converge to the desired solution only if the initial guess is really close to the sought root, i.e. most of the methods are just locally convergent . In practice, a root‐finding algorithm starting from an initial guess 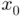moderately far away from the root could easily lead to a sequence 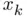that may wander from one point to another of the real axis, eventually diverging to infinity or converging to a solution (not necessarily the sought one). Figure 1.4b illustrates this phenomenon by showing the result of computing the roots of the function 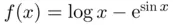using Newton's method starting from different initial guesses. The first two roots of 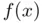are located at 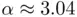and 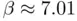(black bullets in Figure 1.4b). In this example, we initialize Newton's method from two initial guesses reasonably close (but not too close) to 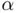. To guide the eye, we have indicated the history of each of the two sequences by encircled numbering of their ordinates. The first sequence starts at 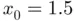(gray square) and Newton's first iterate 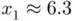is already very close to 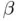, to which the sequence eventually converges (gray dashed lines and symbols). The second sequence starts from 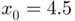(white diamond), unfortunately leading to a location 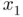where Newton's algorithm predicts a negative second iterate 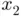, which is not even within the function's domain due to the logarithmic term.

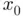From the previous example we can conclude that forecasting the fate of a Newton's sequence based on the location of the initial guess is usually impossible. In the first case, we may have naturally expected the sequence to approach 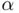instead of 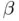(because of its initial proximity to the former one). In the second case, we could have also naturally expected the sequence to converge at least to either one of the two roots, but never such a dramatic failure of the iteration. We recommend the reader to explore the complex convergence properties of Newton's method by starting the iteration from a wide range of initial guesses located between 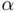and 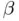. The reader may also repeat the experiment with the secant or chord algorithms to conclude that the behavior of the sequences is also unpredictable when using these methods.

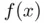Under particular circumstances, there are certain root‐finding methods that always converge to the same root, regardless of the initial guess from which they have been started. In general, for a given function with a unique root 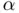in the open interval 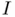, a root‐finding method is said to be globally convergent within 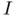if 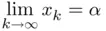for all initial guesses 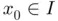. The bisection method or the Regula Falsi 12 method are examples of globally convergent algorithms. However, these and other univariate globally convergent methods are not always easily adaptable to solve systems of nonlinear equations.