Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

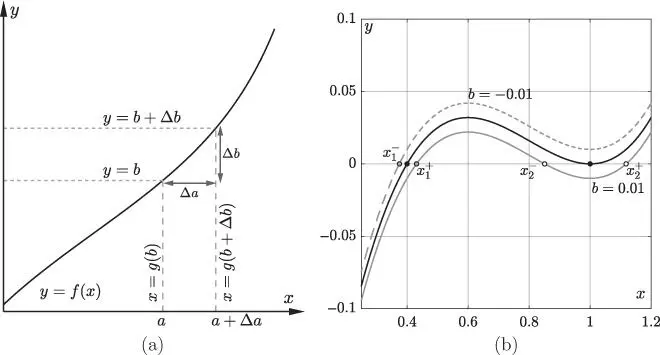
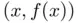Figure 1.3(a) Graph intercepting ordinates 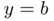and 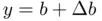at abscissas 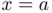and 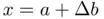, respectively. (b) Roots of the equation 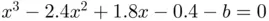for 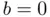(solid black curve), 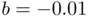(dashed gray), and 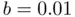(solid gray).

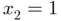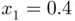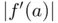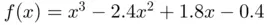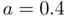From the previous analysis, we can clearly conclude that the double root is more sensitive (or ill‐conditioned) than the simple root . This phenomenon could have been predicted in advance just by evaluating the denominator appearing in ( 1.22) with and or 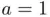, since 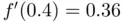, whereas .

In general, for a given numerical problem, it is common practice to quantify its conditioning by the simple relation

(1.23)

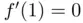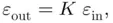
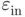where and 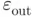are the size of the variations introduced in the input data and their corresponding deviation effect in the outcome solution, respectively, and is a positive constant known as the condition number of the problem. The quantity 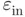may represent uncertainties in the parameters, numerical noise or, within the context of this book, numerical inaccuracies due to limited machine precision. The condition number 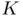must be understood as a noise amplifier , which magnifies small uncertainties. A condition number of order 1 is an indication of well‐conditioning , whereas a problem with 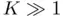is definitely ill‐conditioned .

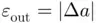By comparing ( 1.23) with ( 1.22), we can easily identify as the displacement exhibited by the root, 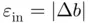as the numerical uncertainty in the evaluation of 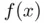, and

(1.24)

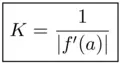
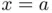as the condition number of the root . As we will see in Section 1.6, the performance of Newton's method can be affected if the root we are looking for is ill‐conditioned.

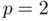Newton's method converges properly only under certain conditions. One required condition is that the initial guess from which the iteration is initiated must be sufficiently close to the root, that is, a local initial guess. In that sense, it is said that Newton's method has only local convergence . Even if the sequence converges to the root, the order may not be always , as in Figure 1.2a.

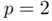It is a common misconception that every single method has its associated local order of convergence (Newton's has , secant has 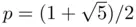, etc.) In actuality, the order also depends on the conditioning of the root to which our sequence approaches. For example, the asymptotic constant from Newton's method 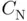appearing in ( 1.16) is proportional to 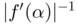. As a consequence, if 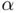is a double root and, accordingly, 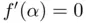, the convergence criterion ( 1.11) is no longer valid since is not bounded. 11