Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

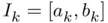Bisection Method: Given such that 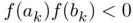, compute 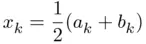and set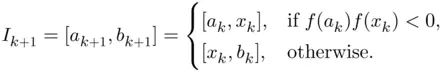

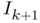This general rule that provides from 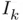is an example of what is generally termed as algorithm , 5 i.e. a set of mathematical calculations that sometimes involves decision‐making. Since this algorithm must be repeated or iterated , the bisection method described above constitutes an example of what is also termed as an iterative algorithm .

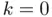Now we revisit the concept of tolerance seen from the point of view of the bisection process. For , the estimation of the root was 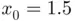, which is the midpoint of the interval 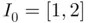, whereas for 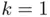we obtain a narrower region of existence of such root, as well as its corresponding improved estimation 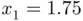. In other words, for 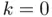the root lies within 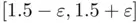, with a tolerance 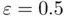, whereas for 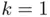the interval containing the root is 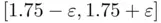, with 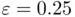. Overall, after 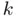bisections, the tolerance is 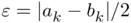, becoming halved in the next iteration.

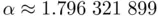If we evaluate the radicals that appear in ( 1.3) with a scientific calculator, we can check that Cardano's analytical solution is approximately . Expression ( 1.3) is mathematically elegant, but not very practical if one needs an estimation of its numerical value. For 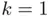we already have that estimation nearly within a 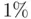or relative error. The reader may keep iterating further to provide better approximations 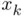of 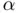, overall obtaining the sequence 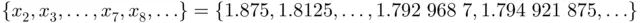. A natural question is whether this sequence has a limit. This leads to the mathematical concept of convergence of a sequence:

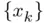Convergence (Exact): The sequence is said to be convergent to 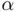if 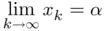or, equivalently, if , where .

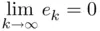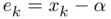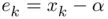The difference appearing in the previous definition is called the error associated with 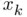. However, since 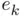may be positive or negative and we are just interested in the absolute discrepancy between 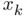and the root 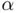, it is common practice to define the absolute error 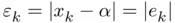of the 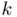th iterate. Checking convergence numerically using the previous definition has two main drawbacks. The first one is that we do not know the value of 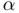, which is precisely the goal of root‐finding. The second is that in practice we cannot perform an infinite number of iterations in order to compute the limit as 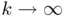, and therefore we must substitute the convergence condition by a numerically feasible one. For example, looking at the sequence resulting from the bisection method, it is clear that the absolute difference of two consecutive elements decreases when increasing 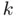(for example, 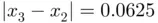and ). Since, by construction, the bisection sequence satisfies 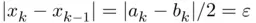, it is common practice to consider a sequence as converged when this difference becomes smaller than a prescribed threshold or tolerance :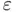