Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers

(1.1)

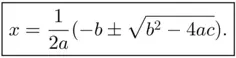
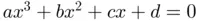An obvious question is whether there is an expression similar to Eq. (1.1) providing the roots or zeros of the cubic equation . The answer is yes, and such expression is usually termed as Cardano's formula . 1 We will not detail here the explicit expression of Cardano's formula but, as an example, if we apply such formulas to solve the equation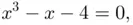

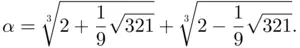
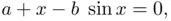
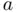(1.2)

we can obtain one of its roots:

(1.3)

There are similar formulas to solve arbitrary quartic equations in terms of radicals, but not for quintic or higher degree polynomials, as proposed by the Italian mathematician Paolo Ruffini in 1799 but eventually proved by the Norwegian mathematician Niels Henrik Abel around 1824.

What we have described is just a symptom of a more general problem of mathematics: the impossibility of solving arbitrary equations analytically. This is a problem that has serious implications in the development of science and technology since physicists and engineers frequently need to solve complicated equations. In general, equations that cannot be solved by means of algebraic methods are called transcendental or nonlinear equations, i.e. equations involving combinations of rational, trigonometric, hyperbolic, or even special functions. An example of a nonlinear equation arising in the field of classical celestial mechanics is Kepler's equation 2

(1.4)

where and 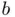are known constants. Another popular example can be found in quantum physics when solving Schrödinger's equation for a particle of mass 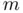in a square well potential of finite depth 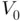and width 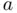. In this problem, the admissible energy levels 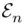corresponding to the bounded states are the solutions of any of the two transcendental equations 3 :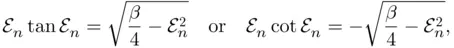

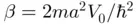(1.5)

where and 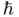is the reduced Planck constant. In this chapter, we will study different methods to obtain approximate solutions of algebraic and transcendental or nonlinear equations such as ( 1.2), ( 1.4), or ( 1.5). That is, while Cardano's formula ( 1.3) provides the exact value 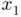of one of the roots of ( 1.2), the methods we are going to study here will provide just a numerical approximation of that root. If you have a rigorous mathematical mind you may feel a bit disappointed since it seems always preferable to have an exact analytical expression rather than an approximation. However, we should first clarify the actual meaning of exact solution within the context of physics.

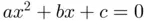It is obvious that if the coefficients appearing in the quadratic equation are known to infinite precision, then the solutions appearing in ( 1.1) are exact. The same can be said for Cardano's solution ( 1.3) of cubic equation ( 1.2). However, equations arising in physics or engineering such as ( 1.4) or ( 1.5) frequently involve universal constants (such as Planck constant 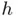, the gravitational constant 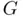, or the elementary electric charge 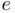). All universal constants are known with limited precision. For example, the currently accepted value of the Newtonian constant of gravitation is, according to NIST, 4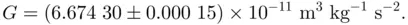

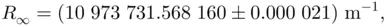
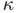As of 2019, the most accurately measured universal constant is

known as Rydberg constant . In other words, the most accurate physical constant is known with 12 digits of precision. Other equations may also contain empirical parameters (such as the thermal conductivity or the magnetic permeability 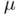of a certain material), which are also known with limited (and usually much less) precision. Therefore, the solutions obtained from equations arising in empirical sciences or technology (even if they have been obtained by analytical methods) are, intrinsically, inaccurate.

Current standard double precision floating point operations are nearly 10 000 times more accurate than the most precise universal constant known in nature. In this book, we will study how to take advantage of this precision in order to implement computational methods capable of satisfying the required accuracy constraints, even in the most demanding situations.