Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers
Здесь есть возможность читать онлайн «Alvaro Meseguer - Fundamentals of Numerical Mathematics for Physicists and Engineers» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Fundamentals of Numerical Mathematics for Physicists and Engineers
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Fundamentals of Numerical Mathematics for Physicists and Engineers: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Fundamentals of Numerical Mathematics for Physicists and Engineers»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Fundamentals of Numerical Mathematics for Physicists and
Engineers
Provides a modern perspective of numerical mathematics by introducing top-notch techniques currently used by numerical analysts Contains two parts, each of which has been designed as a one-semester course Includes computational practicals in Matlab (with solutions) at the end of each section for the instructor to monitor the student's progress through potential exams or short projects Contains problem and exercise sets (also with solutions) at the end of each section is an excellent book for advanced undergraduate or graduate students in physics, mathematics, or engineering. It will also benefit students in other scientific fields in which numerical methods may be required such as chemistry or biology.

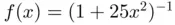 (solid black curve) using equispa... Figure 2.4 Lebesgue functions
(solid black curve) using equispa... Figure 2.4 Lebesgue functions 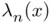 associated with sets of equispaced nodes (2.... Figure 2.5 Interpolation of
associated with sets of equispaced nodes (2.... Figure 2.5 Interpolation of 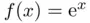 with equispaced nodes. (a)
with equispaced nodes. (a) 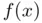 (solid black) and...Figure 2.6 Chebyshev nodes (hollow circles) as the horizontal projection of ...Figure 2.7 Lebesgue functions and constants associated with the Chebyshev no...Figure 2.8 Interpolation of the function
(solid black) and...Figure 2.6 Chebyshev nodes (hollow circles) as the horizontal projection of ...Figure 2.7 Lebesgue functions and constants associated with the Chebyshev no...Figure 2.8 Interpolation of the function 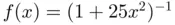 (solid black curve) using Chebysh...Figure 2.9 Interpolation of the function
(solid black curve) using Chebysh...Figure 2.9 Interpolation of the function 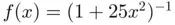 using Chebyshev nodes. (a) Pointw...
using Chebyshev nodes. (a) Pointw...
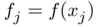 of a ...Figure 3.2 From top to bottom, finite difference formulas (3.3), (3.4), (3.5...Figure 3.3 Centered difference formula (3.5) applied on a set of equidistant...
of a ...Figure 3.2 From top to bottom, finite difference formulas (3.3), (3.4), (3.5...Figure 3.3 Centered difference formula (3.5) applied on a set of equidistant...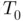 (solid black),
(solid black), 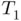 (dashed black),
(dashed black), 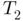 (solid...Figure 4.6 Absolute quadrature error in the Clenshaw–Curtis quadrature appro...Figure 4.7 Computation of the length
(solid...Figure 4.6 Absolute quadrature error in the Clenshaw–Curtis quadrature appro...Figure 4.7 Computation of the length 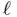 of the ellipse
of the ellipse 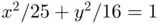 . (a) We compute the ...Figure 4.8 Semi‐logarithmic plot of the absolute quadrature errors correspon...Figure 4.9 Cotangent transformation
. (a) We compute the ...Figure 4.8 Semi‐logarithmic plot of the absolute quadrature errors correspon...Figure 4.9 Cotangent transformation 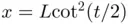 applied on the abscissas
applied on the abscissas 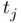 (4.89) for Figure 4.10 Absolute quadrature error
(4.89) for Figure 4.10 Absolute quadrature error 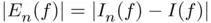 of cotangent quadrature formula (4.8...Figure 4.11 Hyperbolic tangent transformation
of cotangent quadrature formula (4.8...Figure 4.11 Hyperbolic tangent transformation 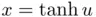 applied on the abscissas
applied on the abscissas 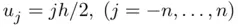 ....Figure 4.12 Absolute quadrature errors
....Figure 4.12 Absolute quadrature errors 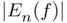 of the approximation of integral (4...
of the approximation of integral (4...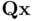 is the reflection of
is the reflection of 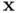 across the line
across the line 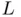 ....Figure 5.3 (a) Properties (5.137). (b) There are two possible reflectors (ac...Figure 5.4 QR‐factorization of a non‐square matrix
....Figure 5.3 (a) Properties (5.137). (b) There are two possible reflectors (ac...Figure 5.4 QR‐factorization of a non‐square matrix 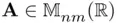 .Figure 5.5 Classical Gram–Schmidt (CGS) algorithm.Figure 5.6 CGS and QR‐factorization equivalence.Figure 5.7 Near parallelism between
.Figure 5.5 Classical Gram–Schmidt (CGS) algorithm.Figure 5.6 CGS and QR‐factorization equivalence.Figure 5.7 Near parallelism between 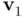 and
and 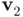 results in a vector
results in a vector 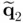 with very ...
with very ...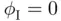 and new solu...Figure 6.5 Continuation methods. (a) Natural continuation fails in the prese...Figure 6.6 Level curve
and new solu...Figure 6.5 Continuation methods. (a) Natural continuation fails in the prese...Figure 6.6 Level curve 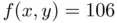 of Himmelblau's function (6.46). (a) Starting the s...
of Himmelblau's function (6.46). (a) Starting the s...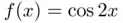 . (a) Fourier coefficients
. (a) Fourier coefficients 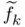 provided by Code 22. (b) Dis...Figure 7.2 Sampling process. (a) The ordinates
provided by Code 22. (b) Dis...Figure 7.2 Sampling process. (a) The ordinates  (gray circles) are the samp...Figure 7.3 (a) The signal
(gray circles) are the samp...Figure 7.3 (a) The signal 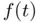 is sampled using
is sampled using 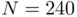 measurements every
measurements every 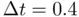 time uni...Figure 7.4 Fourier differentiation of function
time uni...Figure 7.4 Fourier differentiation of function 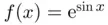 . (a) Sampled function at
. (a) Sampled function at 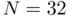 ...Figure 7.5 Exponential convergence of Fourier differentiation of function
...Figure 7.5 Exponential convergence of Fourier differentiation of function 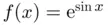 ....Figure 7.6 Differentiation of function
....Figure 7.6 Differentiation of function 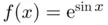 in Fourier space, following Figure ...
in Fourier space, following Figure ...










