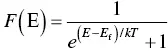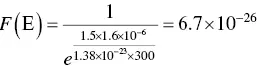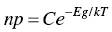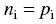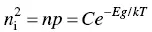George Domingo - Semiconductor Basics

For our purposes, we will look at the results of their quantum statistics: the Fermi–Dirac function, or F‐D function for short, which both scientists developed independently in 1926.

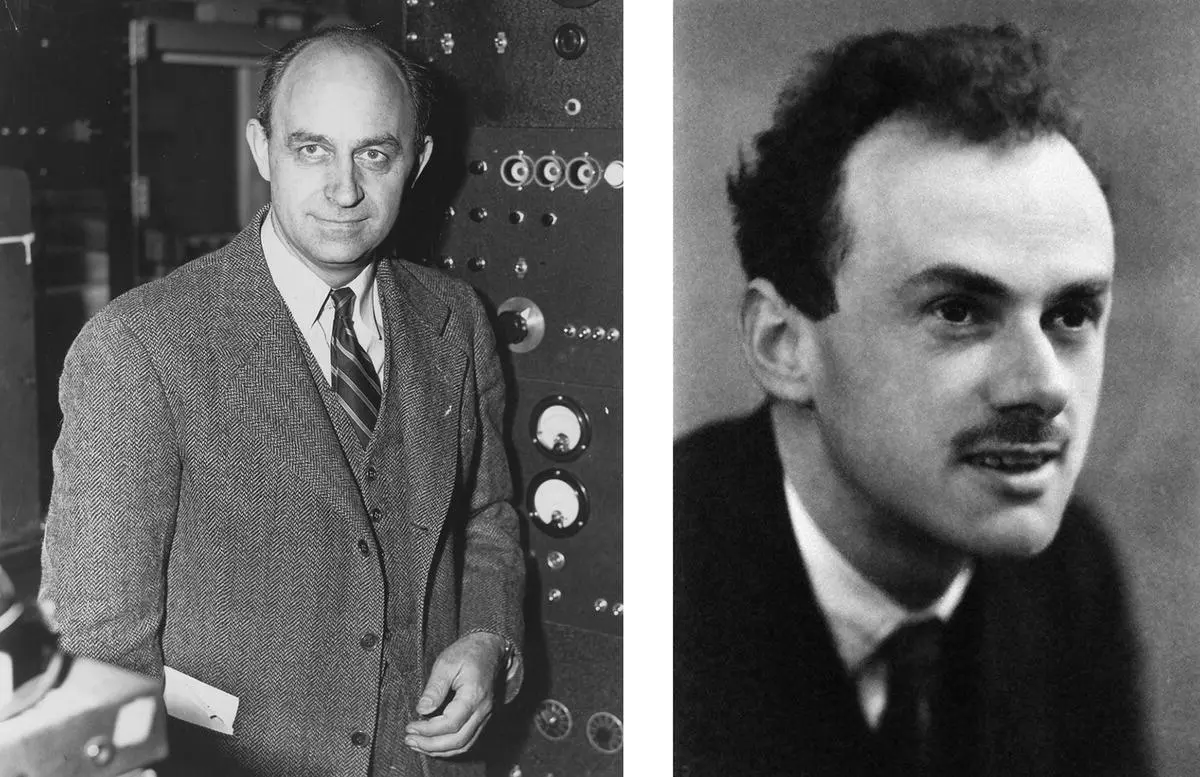
Figure 2.12 Enrico Fermi (left) and Paul Dirac (right), who developed the statistics for particles that obey the quantum physics theory.

Source: https://en.wikipedia.org/wiki/Enrico_Fermi#/media/File:Enrico_Fermi_1943‐49.jpg (left); https://en.wikipedia.org/wiki/Paul_Dirac#/media/File:Dirac_4.jpg (right).

Ludwig Boltzmann (1844–1906), an Austrian physicist, developed his Boltzmann distribution function, which related the behavior of gases and their pressure to their temperature. This applied only to classical particles. The F‐D equation applies the quantum mechanical theory to particles that behave under the Pauli exclusion principle. By the way, these statistics apply to all particles that obey the Pauli exclusion postulate, not just electrons, and these particles are called fermions .

Anyway, the F‐D formula is

(2.1)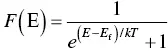

where F (E) is the probability that an energy level E is occupied by an electron, E is the energy of that specific level, E fis the Fermi level, k is the Boltzmann constant ( k = 1.38 × 10 −23m 2kg/s 2T), and T is the temperature in units Kelvin. Note that the only variable for a given energy is the temperature.

At absolute zero, T = 0, the term e (E–E f )/kTis equal to infinity if E < E fand zero if E > E f(remember that e raised to plus infinity is infinity and e raised to minus infinity is zero). Therefore, the F‐D function tells us that at absolute zero all energy levels above E fare empty, and its probability of occupancy is zero, and all energy levels below E fare full, with a 100% probability of being occupied, as I said earlier. As the temperature increases to room temperature (300 K), a slight probability exists that there are some electrons in the higher allowed energy levels, i.e. in the conduction band, and a loss of electrons in the allowed energy levels, the valence band. The F‐D function is symmetrical, as it should be. It confirms mathematically what we saw intuitively and graphically in Figure 2.8. You can see right away that the probability of allowed energy bands greater than 0.1 eV above the Fermi level at 300 K is only 2%, and if we go 0.3 eV above the Fermi level, it goes down to about 10 −7or just one electron in 10 million sites ( Figure 2.13).

Let me now show you graphically how the F‐D statistics represent mathematically exactly what I have just explained. Figure 2.14is the same as Figure 2.13, except that I have exchanged the axes and drawn only one curve: the 300 K (room temperature) curve. Figure 2.14shows that at the Fermi level, the probability of electrons occupying an energy level is 50%, assuming, of course, that there are allowed energy levels in that range. Allowed energy levels higher than the Fermi level have a lower and lower probability of being occupied ( Figure 2.15). As the energy increases, the probability of having an electron occupying a valid energy level decreases, quickly going to zero. If the energy decreases, the opposite is true: at some point, 100% of all the allowed energies will be occupied by electrons. This F‐D curve at 300 K never changes. To change the shape, we need to change the temperature, as shown in Figure 2.13. In Figure 2.15, notice that the F‐D functions on the right for each energy band are identical to each other and also identical to the one in Figure 2.14, except that they are smaller to fit the figure. In the case of the insulator (A), the probability that there are any electrons in the conduction band is as close to nothing as it can get, if you consider that the energy gap is 3 eV, the Fermi level is in the middle, and the difference between the lowest level and the Fermi level is 1.5 eV. If I insert this energy difference in Eq. (2.1), I get the probability that the lowest energy in the conduction band is occupied:

(2.2)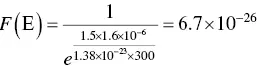

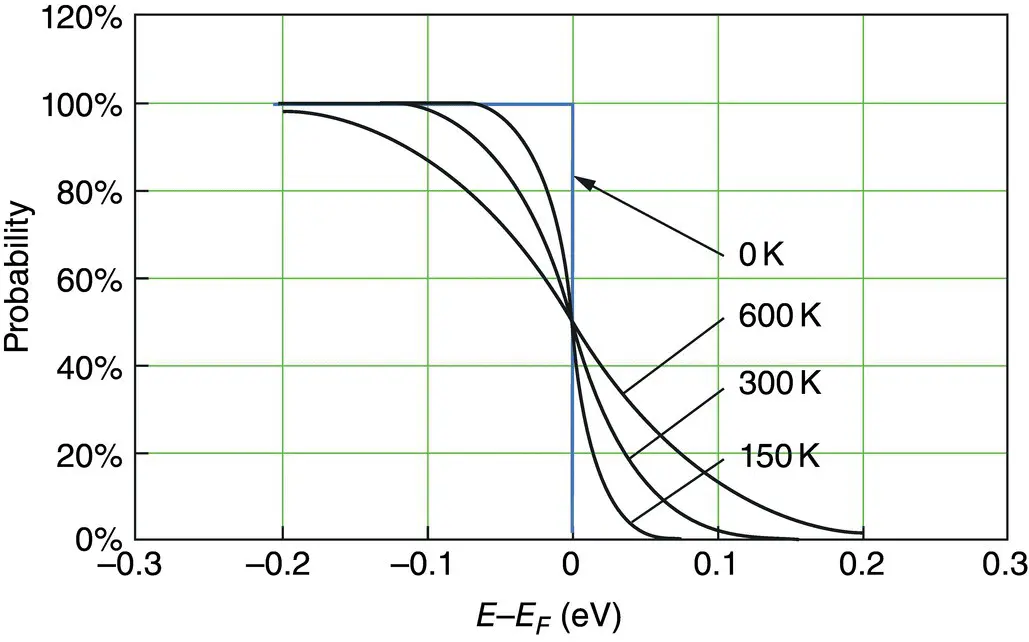
Figure 2.13 The probability that electrons are free as a function of the difference between their energy and the Fermi energy. As the temperature increases, the probability that there are free particle also increases.

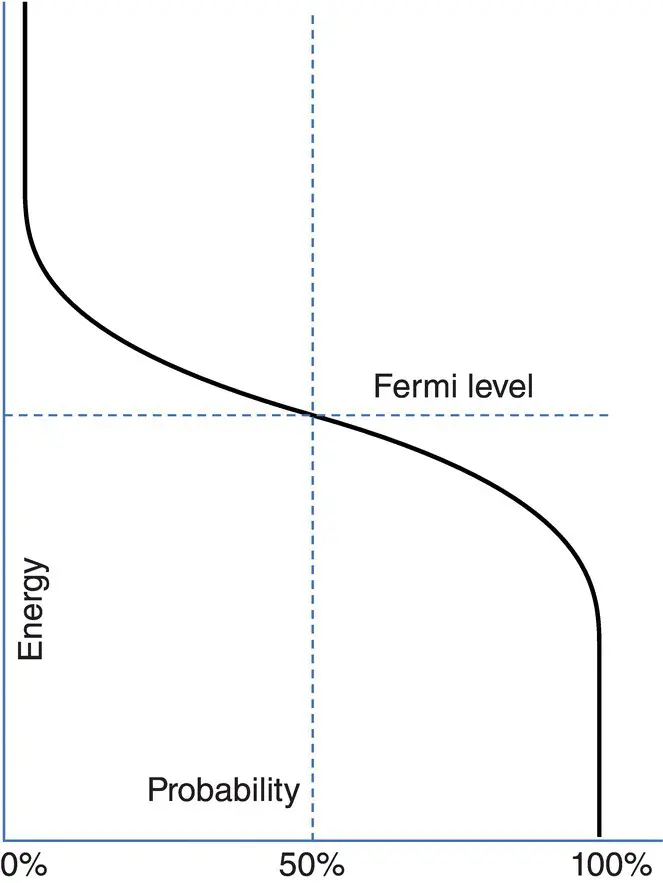
Figure 2.14 The F‐D function at room temperature.

Figure 2.15 The F‐D functions on the side of the energy bands of insulators (A), conductors (B), and semiconductors (C) show how many electrons and holes will be at any of the energy values.

This is practically nothing at all.

The case of the conductor (B) is exactly the opposite. At room temperature, the lower energies of a conductor's conduction band are full of electrons, and the valence band has lots of empty sites, that is, holes.

The semiconductor (C) is in the middle. Very few electrons have energies large enough to be in the conduction band. Silicon has an energy gap equal to 1.11 eV. So, since the Fermi level is in the middle, the lowest energy of the silicon's conduction band is 0.555 eV above the Fermi level. If I use this number in Eq. (2.1), the probability that there is an electron in this lowest of the allowed energy location is 5 × 10 −10: very low, but not zero, as I mentioned in Section 2.4.

The same statistical analysis tells us that the product of electrons and holes is given by

(2.3)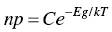

where C is a constant, Eg is the energy difference between the conduction and valence bands (that is, the energy gap), k is the Boltzmann constant, and T is the temperature in degrees Kelvin. Notice that C , Eg , and k are all constants. The only variable in this equation is the temperature, T . In an intrinsic semiconductor – that is, one without any impurities whatsoever – the number of electrons must be identical to the number of holes:

(2.4)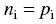

Therefore,

(2.5)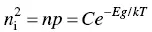

that is, the product of the number of free electrons and free holes in a material is always the same at a given temperature.