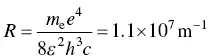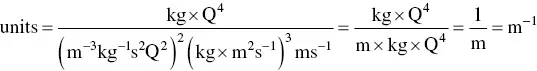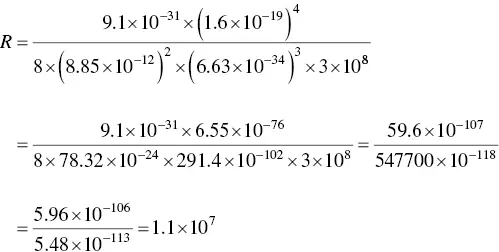George Domingo - Semiconductor Basics

Based on previous theoretical and experimental work, Bohr proposed his planetary model of the atom with discrete and stable energy levels. His model included all the developments of atomic theory known to that date and explained the previous optical observations and measurements beautifully by considering how electrons move from one level to another by accepting or releasing packets of energy.

If you are comfortable with these conclusions, you are ready to go to the next chapter. You may peruse the three following appendices for a few more details.

Four quantum numbers uniquely define an electron:

The principal quantum number, n, defines the orbits and, therefore, the energy of the electrons. The energy released or absorbed as the electrons change orbits is determined exclusively by the value of n. The allowed values of n are any positive integers: 1, 2, 3, 4, etc.

Electrons have two spins: up and down.

Electrons also have angular momentum. The angular quantum number, ℓ, is associated with the shape of the orbits. The value of ℓ is also an integer number between 0 and n.

The magnetic quantum number, ml, is associated with the orientation of the orbits. It is also an integer number between –ℓ and +ℓ.

Electrons follow these rules:

The electrons in the first orbit, n = 1, can have two spins, but both ℓ and ml are 0. Thus the first orbit can hold only two electrons.

The electrons in the second orbit, n = 2, can have two spins and two angular quantum numbers (ℓ equal to 0 or 1). Associated with ℓ = 0, only one ml value is possible, ml = 0. But for ℓ = 1, there are three possible values of ml: −1, 0, and +1. So, the total number of electrons in the second orbit is eight: that is, four ml times two spins each.

You can do the calculations and prove that the third orbit can hold up to 18 electrons, and so on.

Figure 1.16shows one way of visualizing these levels, including the relative energy of the orbits of the Bohr atom and the order in which the orbits are filled. At 0 K absolute temperature, the electrons first fill up the 1s band (two electrons), the next two electrons reside in the 2s band, and the next six are in the 2p band, etc., climbing up the energy level stairs. Note that level 4s fills up before 3d. (By the way, the letters mean s for sharp, p for principle, d for diffuse, and f for fundamental.)

Another point you may wonder about is why we write the 3d level at higher energy than the 4s level. There is quite a debate about explaining this. It has to do with the attraction and repulsion of electrons and protons, and I will leave it at that.

Figure 1.16 Subshell electron capacity. Notice that the number of sites in each level increases as the energy level, n , increases. Also notice that the 3d level has lower energy than the 4s level.

Figure 1.17shows the portion of the periodic table that contains the elements used in semiconductors, showing how many electrons are in the upper shells. All the lower shells are full. Silicon, for example, has 14 electrons, so the electrons fill up bands 1s (2), 2s (2), 2p (6), 3s (2), and 2p (the last 2). If you superimpose these numbers into Figure 1.16, you see that the two lowest energy levels are full, but energy level n = 3 (s + p) has four electrons, with the possibility of accepting another four (in the 2p level) to complete its orbit.

Consider another element that is used a great deal in semiconductors: antimony, Sb. It has 51 electrons. By looking again at Figure 1.16, we find the last occupied level is 5p, with three electrons. All the lower levels are full. Thus, the last occupied energy level, level 5, has five electrons – two in 5s and three in 5p levels – which gives it a chemical valence of 5. We will use these numbers in the next chapter to explain the difference between insulators, conductors, and semiconductors.

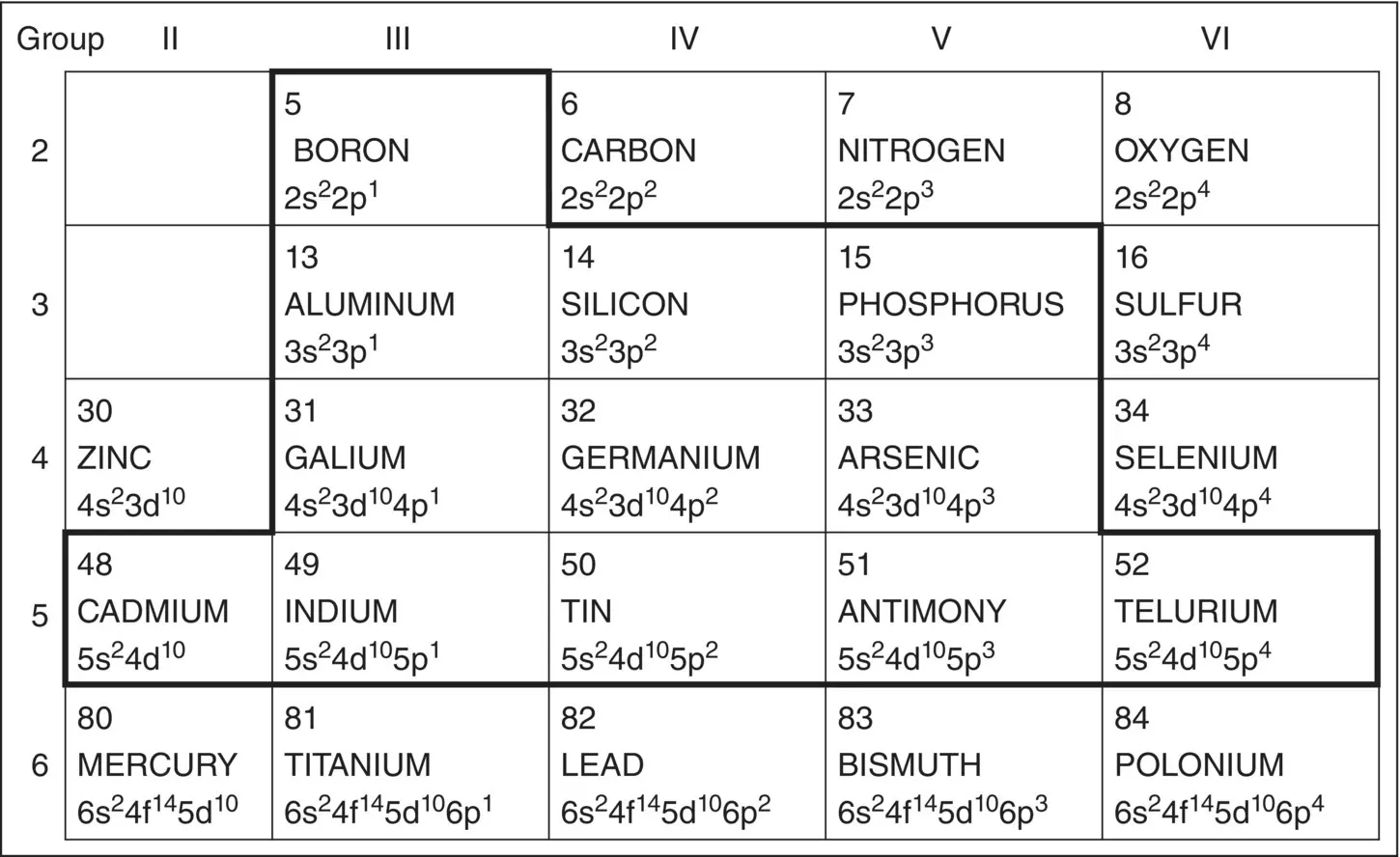
Figure 1.17 Portion of the periodic table emphasizing elements used in semiconductors.

To complete some of the details of this chapter, the Rydberg constant can be calculated from more basic units. It is

(1.6)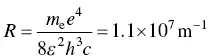

where m eis the mass of the electron ( m e= 9.1 × 10 −31kg), e is the electronic charge ( e = 1.6 × 10 −19C), ε is the permittivity of the material, that is the product of the relative permittivity of the material (e.g. for hydrogen ε r= 253.8) times the permittivity of free space ( ε 0= 8.85 × 10 −12m −3kg −1s 2C 2), h is Planck's constant ( h = 1.06 × 10 −34J s), and c is the speed of light ( c = 3 × 10 8m s −1). All of these quantities are fundamental physical constants.

One thing that we often forget or do not check is the fact that any measurement is composed of a numerical value and a unit. In Eq. (1.6)I show several quantities, each of which has a number and unit(s). The result has to agree with the numerical calculation and the units. Very few people check the units when they perform an operation, which can result in mistakes (remember the fiasco when the Mars orbiter failed because of the confusion between metric and English units). So, let me do this with Eq. (1.6). First the units:

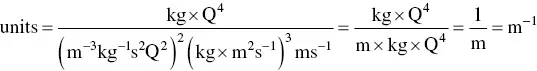
Look at the three terms in the denominator. There are meter (m) terms in the denominator with exponents −6 + 6 + 1 = 1 m, so only one meter unit remains in the denominator. Similarly, with the exponents of the kilograms, there are −2 + 3 = 1 in the denominator. There are four Qs in the denominator, and the seconds in the denominator cancel out (4 – 3 – 1 = 0). Now the kilograms and the coulombs in the numerator cancel those in the denominator, leaving only the reciprocal of a meter as the remaining unit, in agreement with Eq. (1.6).

Now let's do the numbers.

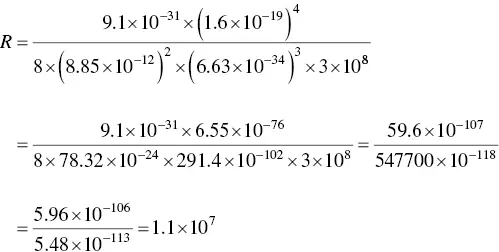
This agrees with the published result.

We saw in the previous chapter that an atom's electrons have precise energy values (we represent them as orbits or levels). We also saw that electrons must have distinct quantum numbers (designations), which limits the number of electrons in an atom that can have a given energy. As atoms have more and more electrons, the electrons have to occupy higher and higher energy levels. An electron must absorb from somewhere the exact energy needed to jump from one level to a higher one. When it falls back to a lower level, it donates the same amount of energy. This is what happens in a gaseous state where the atoms are separated by large distances and do not interact with each other. This model beautifully explains the absorption and emission spectral lines of the elements, the sun, and the stars.