George Domingo - Semiconductor Basics

In this chapter, we are going to push the atoms closer and closer together until we form a solid. Now the atoms and electrons start interacting with each other and forming bonds, which is what keeps them together in a crystallographic structure. As we push them together, the energy levels have to separate because, in a system, according to Pauli's exclusion principle, no two electrons can have the same quantum number. The levels split into bands. Depending on how the bands spread, the material behaves like a conductor, an insulator, or a semiconductor.

Finally, we will analyze the specific case of semiconductors and how the electrons fit into the bands. We will also see how the lack of an electron, which we call a hole , is equivalent to a positive charge.

From the previous chapter, we know that an atom has discrete energy levels, and electrons – unless disturbed by a packet of energy – stay in a stable orbit. We show these energy levels as lines, as in Figure 2.1.

We also saw in the previous chapter that the Pauli exclusion principle states that no two electrons can share the same quantum numbers. If we push together two hydrogen atoms so that they interact and form a single system, the energy levels of the electrons in one atom must have slightly different values than the electrons in the other atom. I show this in Figure 2.2. What was a single level in hydrogen gas, with all the atoms separated by very large distances and acting as independent systems, now becomes two slightly different levels – yes, they are very, very close to each other, but they are still different. This ensures that all the electrons in the system, which is now composed of two atoms, have different quantum numbers.

Figure 2.1 Energy levels in a Bohr atom (left) corresponding to the Bohr energy orbits (right).

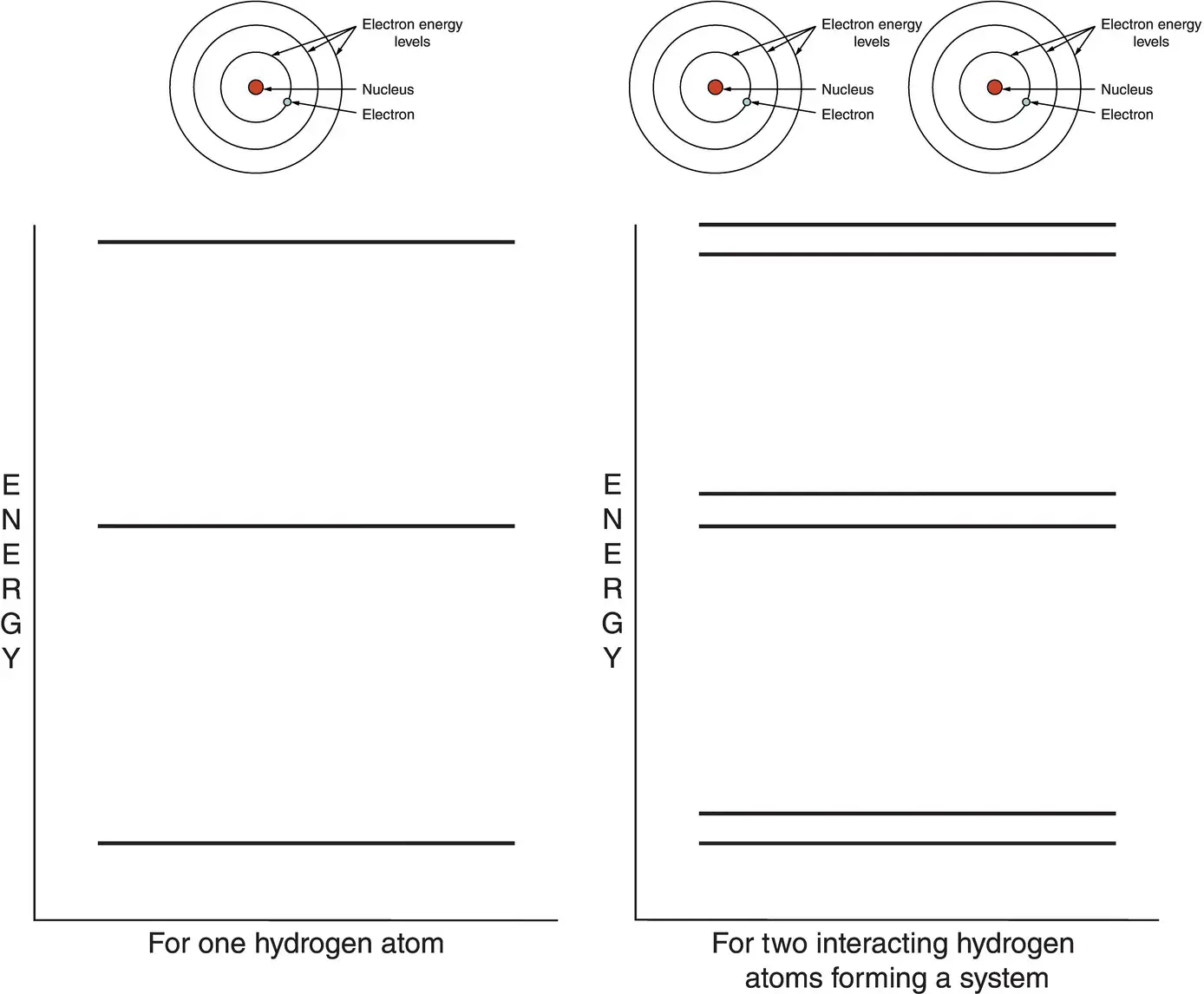
Figure 2.2 When two hydrogen atoms are so close that they form a single system (right), the Pauli exclusion principle requires that their energy levels be different.

Now consider the case of a solid. There are approximately 5 × 10 22silicon atoms per cm 3, that is, a 5 followed by 22 zeros in a space a little smaller than a sugar cube. We can no longer talk about discrete energy levels, as we did with a single hydrogen atom or hydrogen gas. Now we need to talk about energy bands ( Figure 2.3). (Try to draw 10 22lines on a piece of paper!)

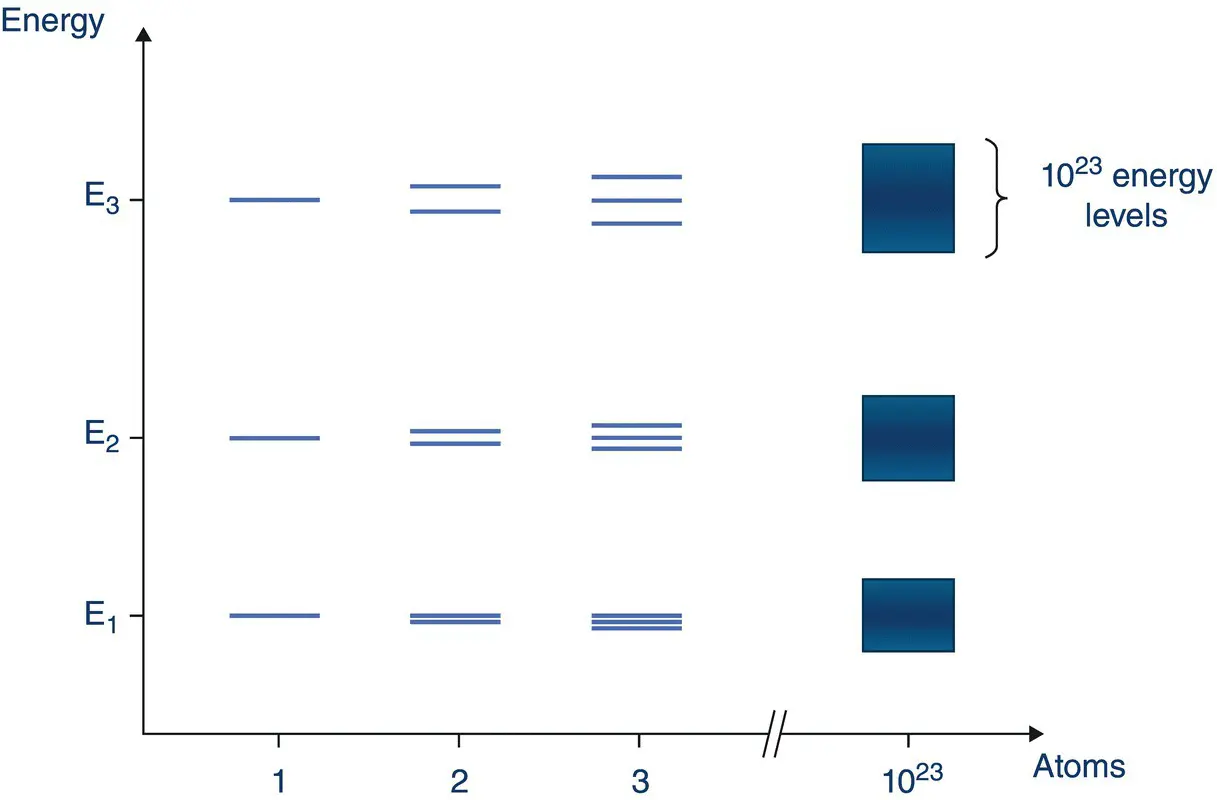
Figure 2.3 From energy levels in a gas where the electrons in the atoms are separated (left) to energy bands in a solid where the atoms are in such proximity that they interact with each other (right).

Energy bands explain the difference between an insulator, a metal, and a semiconductor. Everything depends on how many electrons are in the atom's outer energy level, that is, the valence band level, how the atoms share electrons when they form a solid, and what the separation is between the bands.

Imagine a chamber filled with a gas. The atoms are bouncing around without interfering with each other. Now we start shrinking the chamber, making the distance between atoms – the interatomic distance, a – smaller and smaller ( Figure 2.4).

When a , the interatomic distance, is very large (infinity) at the right of Figure 2.4, the atoms are so far separated that the electrons do not interact with each other. When they are that separated, all the individual atoms have the same energy levels. As the distance between atoms gets smaller, at some point the atoms (beginning with those in the outer orbits) start interacting, and the energy levels begin broadening to satisfy Pauli's exclusion principle. Nature determines the actual interatomic distance, a , in a solid. In silicon, for example, the interatomic distance (called the lattice constant in crystals) is 5.431 angstroms (5.431 Å: an A with a tiny o on top). An angstrom is equal to 1 × 10 −10m.

Note in Figure 2.4that as the interatomic distance gets smaller, the levels start separating in different ways. At the solid's equilibrium spacing, the separation between the first and second bands, A and B, is very large; between the second and third levels, B and C, there is a separation, but it is much smaller. Finally, there is no separation between the third, fourth, and fifth bands (C, D, and E). They encroach on each other. This is expected, because the electrons in the outer bands start to interact before the inner ones do.

At absolute zero (0 K, –273°C, –460°F), there is no energy whatsoever in the system, and all electrons are at the lowest allowed orbit; in a solid, they are all in the lowest possible energy band. We call the highest energy band occupied with some electrons at 0 K the valence band, and we call the next energy band above it – which is totally empty of electrons – the conduction band. You'll see why in a minute. We call the energy separation between the two bands the energy gap ( Eg ) because no electrons are allowed to have these in‐between energies. Here are all the possible cases at absolute zero:

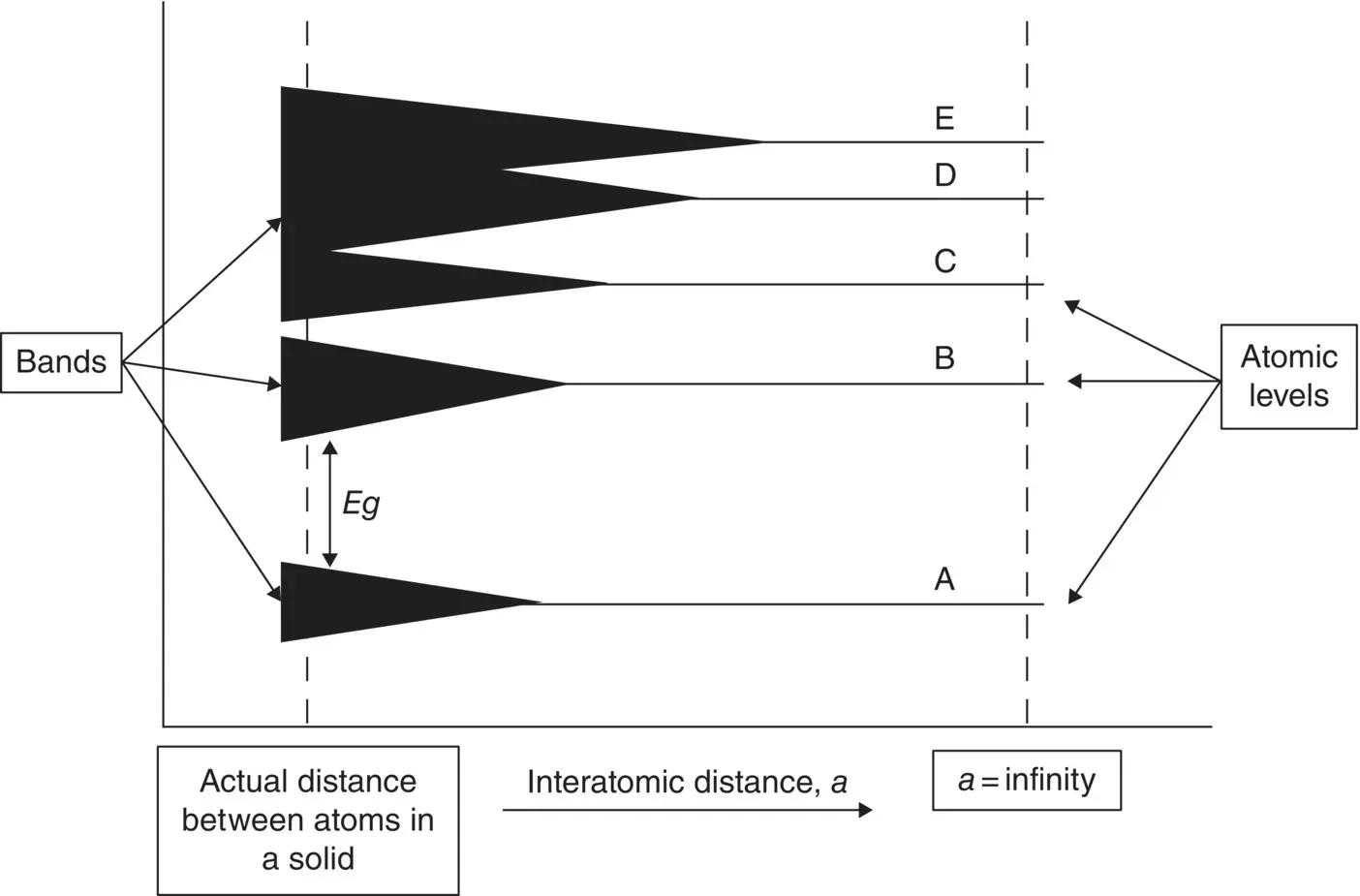
Figure 2.4 Atomic levels split into bands as the interatomic distance between atoms becomes smaller, forming energy bands and energy gaps as soon as they are close enough to interact with each other.

1 The valence band is full of electrons; there is no space for any more.

2 The valence band is not full of electrons. There are empty spaces that can accept additional electrons.

3 The conduction band is separated from the valence band with a small energy gap, such as the separation of levels B and C.

4 The conduction band is separated from the valence band with a large energy gap, such as that between A and B.

5 There is no separation at all between two bands such as C and D or D and E. The conduction band touches or falls inside the valence band.

Let's take a look at each of these cases.

Let's consider first the situation in which the valence band is full of electrons (case 1) and there is a large gap separating the valence and conduction bands (case 4). I illustrate this in Figure 2.5. Imagine that the valence band is a parking lot full of cars (electrons), and above it is the conduction band, equivalent to an empty freeway. The cars in the parking lot cannot move because there is no space for them to go to. No cars are on the freeway, so there is no movement up there, either. If I apply a voltage to this material (right, in Figure 2.5), nothing moves. The gap between the parking lot and the freeway is too large for cars to jump, and thus no matter what voltage I apply, the electrons cannot move; there is no current flowing in this material at all. This is the case for insulators . No electrons can move under an applied voltage.

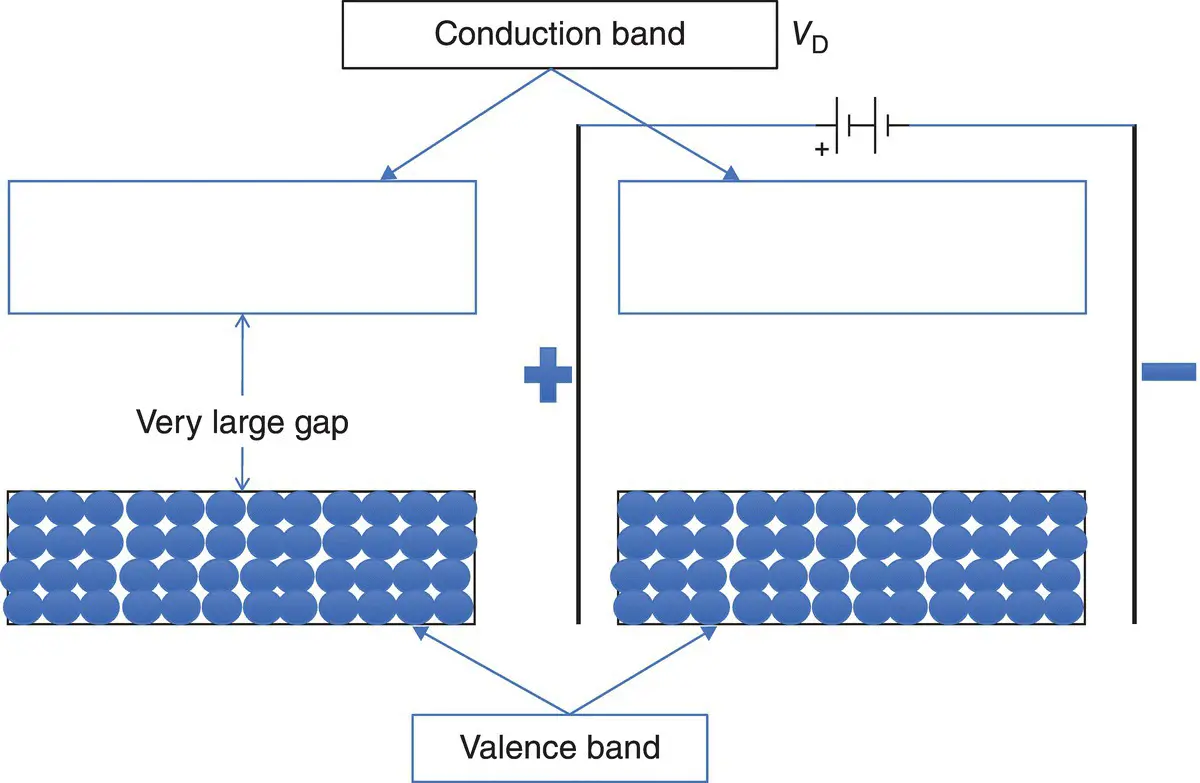
Figure 2.5 In an insulator, the valence band is full of electrons, the conduction band is empty, and the separation between the two bands is very large.