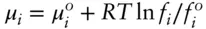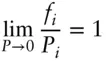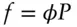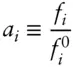2 At the opposite end is the case where Xi is very small. Here interactions between component i molecules are extremely rare, and the behavior of μi is essentially controlled by interactions between i and those of the solvent. While the behavior of μi is not ideal, it is nonetheless a linear function of ln Xi. This is the region where Henry's law holds. Let's define the constant η (eta) such that for conditions where Henry's law holds: Figure 3.8 Schematic plot of the chemical potential of component i in solution as a function of ln Xi. Here μ° is the chemical potential of pure i at the pressure and temperature of the diagram. After Nordstrom and Munoz (1986).(3.38) Comparing this equation with eqn. 3.10, we see that η is merely another form of the Henry's law constant; whereas h has units of pressure, η is dimensionless. The compositional dependence of the chemical potential in the Henry's law region can be expressed as:(3.39) This equation can be rewritten as:(3.40) By definition, η is independent of composition at constant T and P and can be regarded as adding or subtracting a fixed amount to the standard state chemical potential (a fixed amount to the intercept in Figure 3.8). By independent of composition, we mean it is independent of Xi, the mole fraction of the component of interest. η will depend on the nature of the solution. For example, if Na is our component of interest, ηNa will not be the same for an electrolyte solution as for a silicate melt. We can define a new term, μ*, as:(3.41) Substituting eqn. 3.40 into 3.39 we obtain:(3.42) When plotted against ln Xi, the chemical potential of i in the range of very dilute solutions is given by a straight line with slope RT and intercept μ* (the intercept is at Xi = 1 and hence ln Xi = 0 and μi = μ*). Thus, μ* can be obtained by extrapolating the Henry's law slope to X = 1. We can think of μ* as the chemical potential in the hypothetical standard state of Henry's law behavior at X = 1.
3 The third region of the plot is that region of real solution behavior where neither Henry's law nor Raoult's law apply. In this region, μ is not a linear function of ln X. We will introduce a new parameter, activity, to deal with this region.
The tools we have introduced to deal with ideal solutions and infinitely dilute ones are based on observations of the gaseous state: Raoult's law and Henry's law. We will continue to make reference to gases in dealing with real solutions that follow neither law. While this approach has a largely historical basis, it is nevertheless a consistent one. So following this pattern, we will first introduce the concept of fugacity, and derive from it a more general parameter, activity .
In the range of intermediate concentrations, the partial pressure of the vapor of component i above a solution is generally not linearly related to the mole fraction of component i in solution. Thus, the chemical potential of i cannot be determined from equations such as 3.26, which we derived on the assumption that the partial pressure was proportional to the mole fraction. To deal with this situation, chemists invented a fictitious partial pressure, fugacity . Fugacity may be thought of as the “escaping tendency” of a real gas from a solution. It is defined to have the same relationship to chemical potential as the partial pressure of an ideal gas:
(3.43) 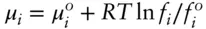
where ƒ° is the standard-state fugacity, which is analogous to standard-state partial pressure. We are free to choose the standard state, but the standard state for ƒ° and μ° must be the same. If we choose our standard state to be the pure substance, then ƒ° is identical to P °, but we may wish to choose some other standard state where this will not be the case. Since the behavior of real gases approaches ideal at low pressures, the fugacity will approach the partial pressure under these circumstances. Thus the second part of the definition of fugacity is:
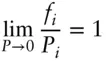
For an ideal gas, fugacity is identical to partial pressure. Since, as we stated above, fugacity bears the same relationship to chemical potential (and other state functions) of a nonideal substance as pressure of a nonideal gas, we substitute fugacity for pressure in thermodynamic equations.
The relationship between pressure and fugacity can be expressed as:
(3.44) 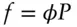
where φ is the fugacity coefficient . The fugacity coefficient expresses the difference in the pressure between a real gas and an ideal gas under comparable conditions. Kerrick and Jacobs (1981) fitted the Redlich–Kwong equation (eqn. 2.15) to observations on the volume, pressure and volume of H 2O and CO 2to obtain values for the coefficients a and b in eqn. 2.15. From these, they obtained fugacity coefficients for these gases at a series of temperatures and pressures. These are given in Table 3.1; Example 3.2illustrates their use.
Table 3.1 H 2O and CO 2fugacity coefficients.
| H 2O |
|
T (°C) |
|
|
| P (MPa) |
400 |
600 |
800 |
1000 |
| 50 |
0.4 |
0.78 |
0.91 |
|
| 200 |
0.2 |
0.52 |
0.79 |
0.94 |
| 400 |
0.21 |
0.54 |
0.84 |
1.03 |
| 600 |
0.28 |
0.67 |
1.01 |
1.22 |
| 800 |
0.4 |
0.89 |
1.27 |
1.49 |
| CO2 |
|
T (°C) |
|
| P (MPa) |
377 |
577 |
777 |
977 |
| 50 |
1.02 |
1.1 |
1.12 |
1.12 |
| 200 |
1.79 |
1.86 |
1.82 |
1.75 |
| 400 |
4.91 |
4.18 |
3.63 |
3.22 |
| 600 |
13.85 |
9.48 |
7.2 |
5.83 |
| 800 |
38.73 |
21.33 |
14.15 |
10.44 |
From Kerrick and Jacobs (1981).
3.6.3 Activities and activity coefficients
Fugacities are thermodynamic functions that are directly related to chemical potential and can be calculated from measured P–T–V properties of a gas, though we will not discuss how. However, they have meaning for solids and liquids as well as gases, since solids and liquids have finite vapor pressures. Whenever a substance exerts a measurable vapor pressure, a fugacity can be calculated. Fugacities are relevant to the equilibria between species and phase components, because if the vapor phases of the components of some solid or liquid solutions are in equilibrium with each other, and with their respective solid or liquid phases, then the species or phase components in the solid or liquid must be in equilibrium. One important feature of fugacities is that we can use them to define another thermodynamic parameter, the activity, a :
(3.45) 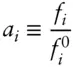
ƒ° is the standard state fugacity. Its value depends on the standard state you choose. You are free to choose a standard state convenient for whatever problem you are addressing.
Читать дальше