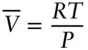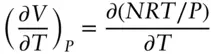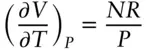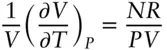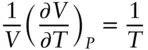Energy is the capacity to produce change. It is a fundamental property of any system, and it should be familiar from physics. By choosing a suitable reference frame, we can define an absolute energy scale. However, it is changes in energy that are generally of interest to us rather than absolute amounts. Work and heat are two of many forms of energy. Heat, or thermal energy, results from random motions of molecules or atoms in a substance and is closely related to kinetic energy. Work is done by moving a mass, M , through some distance, x = X , against a force F :
(2.1) 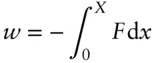
where w is work and force is defined as mass times acceleration:
(2.2) 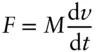
(the minus sign is there because of the convention that work done on a system is positive, work done by a system is negative). This is, of course, Newton's first law. In chemical thermodynamics, pressure–volume work is usually of more interest. Pressure is defined as force per unit area:
(2.3) 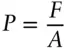
Since volume is area times distance, we can substitute eqn. 2.3and d V = A d x into eqn. 2.1and obtain:
(2.4) 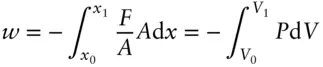
Thus, work is also done as a result of a volume change in the presence of pressure.
Potential energy is energy possessed by a body by virtue of its position in a force field, such as the gravitational field of the Earth, or an electric field. Chemical energy will be of most interest to us in this book. Chemical energy is a form of potential energy stored in chemical bonds of a substance. Chemical energy arises from the forces involved in the interaction between atoms and electrons. Internal energy, which we denote with the symbol U , is the sum of the potential energy arising from these forces as well as the kinetic energy of the atoms and molecules (i.e., thermal energy) in a substance. It is internal energy that will be of most interest to us.
We will discuss all these fundamental variables in more detail in the next few sections.
2.2.2 Properties of state
Properties or variables of a system that depend only on the present state of the system, and not on the manner in which that state was achieved, are called variables of state or state functions . Extensive properties depend on total size of the system. Mass, volume, and energy are all extensive properties. Extensive properties are additive, the value for the whole being the sum of values for the parts. Intensive properties are independent of the size of a system, for example temperature, pressure, and viscosity. They are not additive, for example, the temperature of a system is not the sum of the temperature of its parts. In general, an extensive property can be converted to an intensive one by dividing it by some other extensive property. For example, density is the mass per volume and is an intensive property. It is generally more convenient to work with intensive rather than extensive properties. For a single component system not undergoing reaction, specification of three variables (two intensive, one extensive) is generally sufficient to determine the rest, and specification of any two intensive variables is generally sufficient to determine the remaining intensive variables.
A final definition is that of a pure substance . A pure substance is one that cannot be separated into fractions of different properties by the same processes as those considered. For example, in many processes, the compound H 2O can be considered a pure substance. However, if electrolysis were involved, this would not be the case.
Equations of state describe the relationship that exists among the state variables of a system. We will begin by considering the ideal gas law and then very briefly consider two more complex equations of state for gases.
The simplest and most fundamental of the equations of state is the ideal gas law . *It states that pressure, volume, temperature, and the number of moles of a gas are related as:
(2.5) 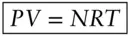
where P is pressure, V is volume, N is the number of moles, T is thermodynamic, or absolute temperature (which we will explain shortly), and R is the ideal gas constant †(an empirically determined constant equal to 8.314 J/mol-K, 1.987 cal/mol-K, or 82.06 cc-atm/deg-mol). This equation describes the relation between two extensive (mass-dependent) parameters, volume and the number of moles, and two intensive (mass-independent) parameters, temperature and pressure. We earlier stated that if we defined two intensive and one extensive system parameter, we could determine the remaining parameters. We can see from eqn. 2.5that this is indeed the case for an ideal gas. For example, if we know N , P , and T , we can use eqn. 2.5to determine V .
The ideal gas law, and any equation of state, can be rewritten with intensive properties only. Dividing V by N we obtain the molar volume , 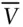 . Substituting
. Substituting 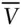 for V and rearranging, the ideal gas equation becomes:
for V and rearranging, the ideal gas equation becomes:
(2.6) 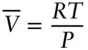
The ideal gas equation tells us how the volume of a given amount of gas will vary with pressure and temperature. To see how molar volume will vary with temperature alone, we can differentiate eqn. 2.6with respect to temperature, holding pressure constant, and obtain:
(2.7) 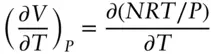
which reduces to:
(2.8) 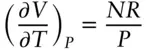
It would be more useful to know the fractional volume change rather than the absolute volume change with temperature, because the result in that case does not depend on the size of the system. To convert to the fractional volume change, we simply divide the equation by V :
(2.9) 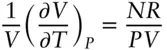
Comparing eqn. 2.9with eqn. 2.5, we see that the right-hand side of the equation is simply 1/ T , thus
(2.10) 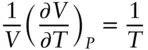
The left-hand side of this equation, the fractional change in volume with change in temperature, is known as the coefficient of thermal expansion, α:
Читать дальше

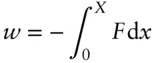
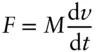
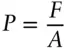
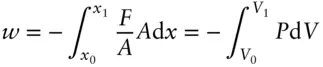
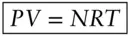
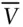 . Substituting
. Substituting 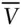 for V and rearranging, the ideal gas equation becomes:
for V and rearranging, the ideal gas equation becomes: