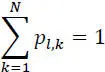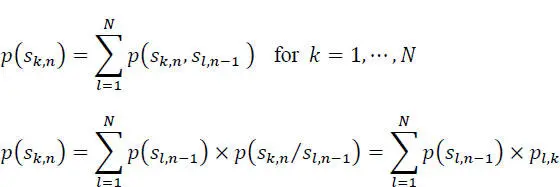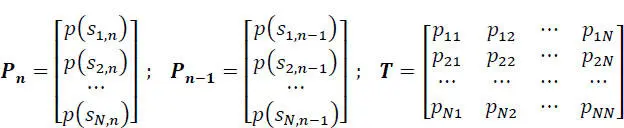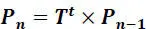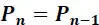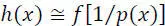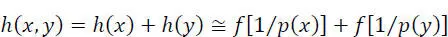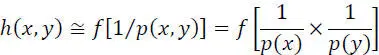2
Measurement of Information of a Discrete Source and Channel Capacity
2.1. Introduction and definitions
The purpose of a message is to provide information to a recipient. Information, like energy, for that matter, is a fundamental notion, which is part of our daily life. It can be transported (transmitted), stored (memorized) and transformed (processed).
The value of information lies in the surprise effect it causes; it is all the more interesting because it is less predictable . As a result, information is assimilated to an event of a random nature, considered, in the following, as a random variable.
The measure of the information is then given by measuring the uncertainty of an event system , that is to say, the random choice of an event in a set of possible and distinct events.
We will use the terms message or sequence to indicate any finite sequence of symbols taken in an alphabet A = { } of a discrete source: a finite set of predetermined symbols, for example:
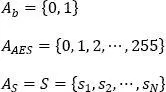
We will use the term discrete source of information Sn to indicate the system selecting, from the set of symbols from As = S , the symbols to transmit:
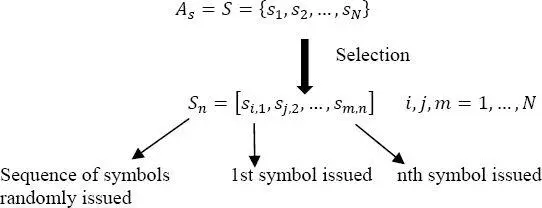
The choice of sm,n is carried out according to a given probability law, which can be steady temporally or variable over time.
2.2. Examples of discrete sources
2.2.1. Simple source (memoryless)
This is a source for which the probability of the occurrence of a symbol does not depend on the previous symbols:
[2.1] 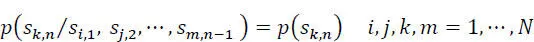
[2.2] 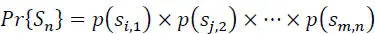
2.2.2. Discrete source with memory
It is a source for which the probability of occurrence of a symbol depends on the symbols already emitted (statistical dependence) and on instants 1, 2, ..., n where they have been emitted:
[2.3] 
If the source is in addition stationary then the dependence is only on the ranks and not on the moments when the symbols have been transmitted, so:
[2.4] 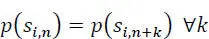
that is, the statistical properties are independent of any temporal translation . We can consider that a text written in any language is an example of such a source.
2.2.3. Ergodic source: stationary source with finite memory
The ergodicity of an information source implies that a temporal average calculated over an infinite duration is equal to the statistical average.
2.2.4. First order Markovian source (first order Markov chain)
First order Markov sources play an important role in several domains, for example, in (Caragata et al . 2015), the authors used such a source to model the cryptanalysis of a digital watermarking algorithm.
It is characterized by:
[2.5] 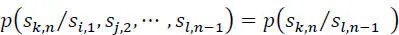
with:
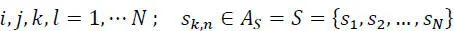
The probability 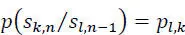 = pl,k is called transition probability from state l to state k , and:
= pl,k is called transition probability from state l to state k , and:
[2.6] 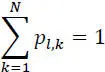
The probability that at time n the source is in the state k is:
[2.7] 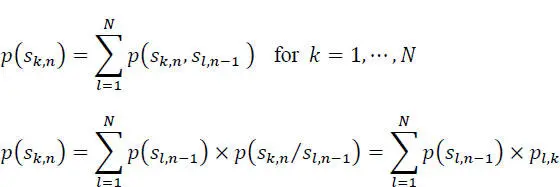
By introducing matrix notations:
[2.8] 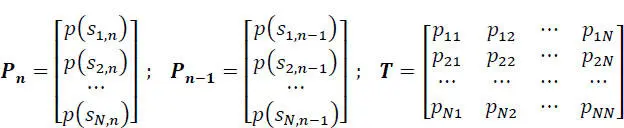
Taking into account the relationship [2.8], the relation [2.7]is also written as:
[2.9] 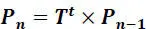
where Tt is the transposed matrix of transition probabilities.
Moreover, if the source is, stationary, then:
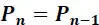
in other words, the probabilities of the occurrence of the symbols do not depend on n. It is the same for the transition probabilities pl,k , then the relation [2.9]is written:
[2.10] 
where P 0is the matrix of probabilities governing the generation of symbols by the source at the initial instant n = 0.
2.3. Uncertainty, amount of information and entropy (Shannon’s 1948 theorem)
The realization of an event x of probability p(x) conveys a quantity of information h(x) related to its uncertainty. h(x) is an increasing function of its improbability 1/ p ( x ):
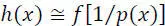
If an event x is certain, then p( x ) = 1, the uncertainty is zero and therefore the quantity of information h( x ) brought by its realization is null.
Moreover, let us consider the realization of a pair of independent events x and y . Their joint realization leads to the amount of information it brings being the sum of the quantities of information brought by each of them:
[2.11] 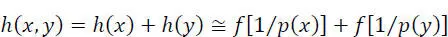
but ft( x,y ) is also written:
[2.12] 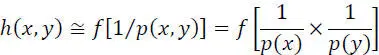
Читать дальше

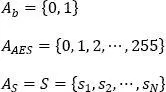

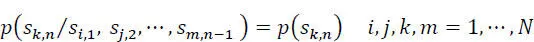
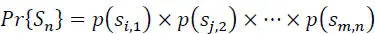

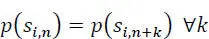
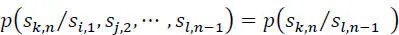
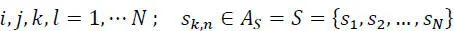
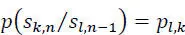 = pl,k is called transition probability from state l to state k , and:
= pl,k is called transition probability from state l to state k , and: