Ross Anderson - Security Engineering

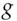The first public-key encryption scheme to be published, by Whitfield Diffie and Martin Hellman in 1976, has a fixed primitive root and uses 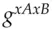modulo 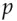as the key to a shared-key encryption system. The values 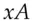and 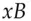can be the private keys of the two parties.

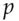Let's walk through this. The prime and generator 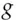are common to all users. Alice chooses a secret random number 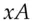, calculates 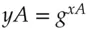and publishes it opposite her name in the company phone book. Bob does the same, choosing a random number 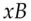and publishing 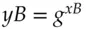. In order to communicate with Bob, Alice fetches 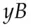from the phone book, forms 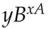which is just 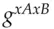, and uses this to encrypt the message to Bob. On receiving it, Bob looks up Alice's public key 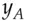and forms 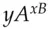which is also equal to 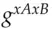, so he can decrypt her message.

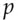Alternatively, Alice and Bob can use transient keys, and get a mechanism for providing forward security. As before, let the prime and generator 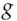be common to all users. Alice chooses a random number 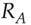, calculates and sends it to Bob; Bob does the same, choosing a random number 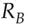and sending 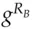to Alice; they then both form 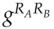, which they use as a session key (see Figure 5.18).

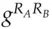Alice and Bob can now use the session key to encrypt a conversation. If they used transient keys, rather than long-lived ones, they have managed to create a shared secret ‘out of nothing’. Even if an opponent had inspected both their machines before this protocol was started, and knew all their stored private keys, then provided some basic conditions were met (e.g., that their random number generators were not predictable and no malware was left behind) the opponent could still not eavesdrop on their traffic. This is the strong version of the forward security property to which I referred in section 5.6.2. The opponent can't work forward from knowledge of previous keys, however it was obtained. Provided that Alice and Bob both destroy the shared secret after use, they will also have backward security: an opponent who gets access to their equipment later cannot work backward to break their old traffic. 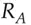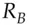In what follows, we may write the Diffie-Hellman key derived from and as 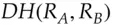when we don't have to be explicit about which group we're working in, and don't need to write out explicitly which is the private key 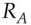and which is the public key .

Figure 5.18 : The Diffie-Hellman key exchange protocol

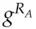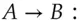
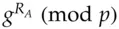
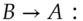
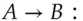
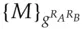
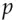Slightly more work is needed to provide a full solution. Some care is needed when choosing the parameters and 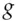; we can infer from the Snowden disclosures, for example, that the NSA can solve the discrete logarithm problem for commonly-used 1024-bit prime numbers 6. And there are several other details which depend on whether we want properties such as forward security.