Yong Bai - Deepwater Flexible Risers and Pipelines

In order to get acceptable results from FEM, points which are not in correspondence of the gaps between wires are chosen to investigate the contact pressure, and the selected points are shown in Figure 4.19.

The average results among the outcomes are compared to the theoretical ones, as shown in Figures 4.21and 4.22. As they show good accordance, Eq. (4.9)could be used as a rough estimation to carry out the contact pressure between the two different layers.

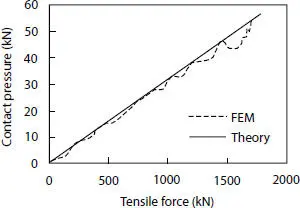
Figure 4.21 Contact pressure between pressure armor and inner tensile armor layer.

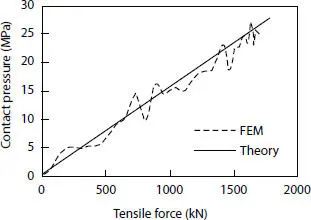
Figure 4.22 Contact pressure between tensile armor layers.

The evaluation in terms of stresses regards the tensile armor is conducted, being the one that provides most of the strength in the longitudinal direction. The theoretical model assumes that strain and stress is axisymmetric, i.e., the stress for all the wires at the same pipe cross section is assumed to be the same. Von Mises stress contour plot of the outer tensile armor layer is shown in Figure 4.23, with its active view cut in z plane. Selecting the points from all the wires located at the mid-span and comparing their stresses and strain with the theoretical results as shown in Figure 4.24, it can be observed that, even if there are some fluctuations, their amplitude is still not high.

A random wire from each layer was chosen to conduct the comparison between the Mises stress and the elongation, as shown in Figures 4.25and 4.26. The comparison between the trends leads to a remarkable confidence in terms of stress behavior.

Once the validity of the theoretical model is proved, it is extended in order to consider the contribution of the external pressure. Longitudinal displacements are applied at a constant rate until 20 mm, while constant pressure equal to 20 MPa is applied on the outer surface of the tensile armor layer. Only the contribution of the tensile armor is considered as previously explained in Figure 4.20. As it was expected, the presence of the pressure armor in the profile of the pipe makes the structure stiff enough in radial direction so that the hydrostatic pressure does not affect the tensile capacity of the pipe in a notable way, which is just slightly reduced, as shown in Figure 4.27, where T stands for pure tensile load and TP stands for combined tensile and external pressure loads.

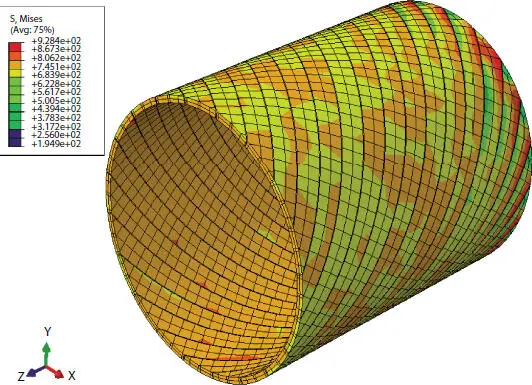
Figure 4.23 Mises stress—outer layer of wires.

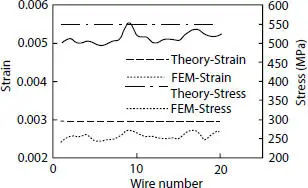
Figure 4.24 Strain and stress distribution for outer tensile armor layer.

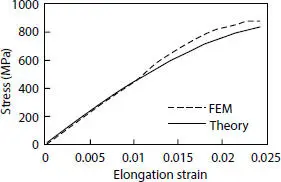
Figure 4.25 Mises stress comparison for inner tensile armor layer.

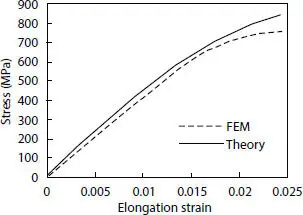
Figure 4.26 Mises stress comparison for outer tensile armor layer.

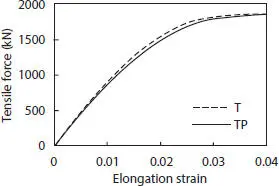
Figure 4.27 Tensile strength comparison for the pipe subjected to pure tension and combined external and tensile loads.

In this section, the reference case of “metallic strip flexible pipes” subjected to pure tensile load is included, which is regarded as Case 1. The study has already been developed in [16] for a range of MSFP which does not include the pressure armor layer in the profile. It has been observed that, found out that, for this kind of pipe, the tensile force is mainly due to the PE layers.

Based on MSFP’s structure, the extra pressure armor layer is added in its inner reinforcement cross-section design, regarded as Case 2. As previously shown, the contribution to the overall radial stiffness induced by the pressure armor allows the possibility of neglecting the innermost and outermost HDPE layers. The tensile armor layers, existing in Case 3, are substituted by four steel strip reinforced layers accounting for thickness h = 0.5 mm. The detailed longitudinal profile of Case 2 is illustrated in Figure 4.28. For this numerical campaign, the inner diameter and the loading condition are the same as the previous case. The theoretical model is extended to the new geometry, for which the coefficients expressed in Eqs. (4.11)and (4.12)should be modified by considering the variation in terms of number of layers and thickness, which can be expressed as

(4.15)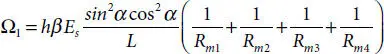

(4.16)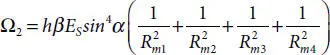

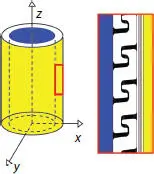
Figure 4.28 MSFP-based reinforced longitudinal profile.

Tensile forces comparison for those pipes with three different configurations is shown in Figure 4.29. As expected, the strength provided by MSFP is the lowest. In fact, for the same inner diameter, the MSFP shows a decrement in axial resistance equal to 81.07% compared to the case which includes two tensile armor layers. At the same time, it is possible to see the improvement in terms of tensile capacity when the pressure armor is included in the MSFP design equal to 81.53%, which results from the comparison between Case 1 and Case 2. When both the pressure and tensile armor layers are included in the design, the high strength in radial direction is not only provided by the pressure armor but also by the tensile armor due to its relevant thickness. Thus, reducing the thickness of the wires not only affects the tensile capacity itself but also the loss of the external capacity.

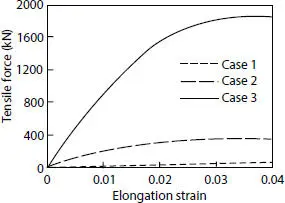
Figure 4.29 Tensile force comparison.

Being the elongation of the pipe strictly related to its weight, which mostly depends on the amount of the reinforcement needed as well as the water depth, it is possible to assert that the steel strip reinforcements in terms of axial strength of the pipe are suitable for shallow waters. On the other hand, the contribution of thick steel wires is suitable for extreme loading conditions such as for deep water design. It is noteworthythat for both Cases 2 and 3, the contribution of the radial stiffness induced by pressure armor plays an important role in terms of axial capacity of the pipe.