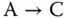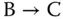DNA- and RNA-Based Computing Systems

Take the addition a + b = c as an example. The corresponding chemical reactions are designed as

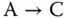
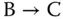
where the concentrations of molecular types A, B, and C represent the values of a , b , and c , respectively. As both the inputs A and B are transferred to C, the concentration of C is the sum of the initial concentrations of A and B, namely, the values of a and b .

Digital signal processing (DSP) modules such as filters and fast Fourier transform (FFT) processors are of good importance and perform a wide variety of functions. CRN is a novel alternative to traditional application‐specific integrated circuits (ASICs) to implement DSP algorithms since they are also applicable to the field of molecular computing. Methods for implementing DSP algorithms using synchronous, RGB, and asynchronous schemes have been demonstrated in detail by [23,24,33,34] (Figures 3.7and 3.8).

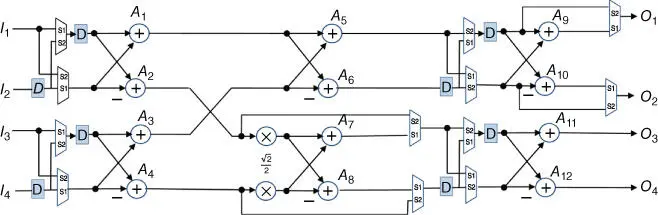
Figure 3.7A folded eight‐point four‐parallel real‐valued FFT processor.

Source: From Jiang et al. [25]. Reproduced with the permission of American Chemical Society.

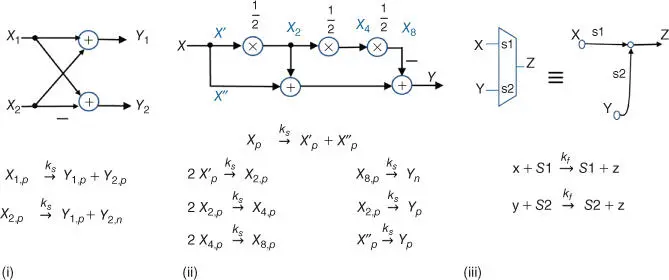
Figure 3.8Molecular reactions for each element of the FFT processor in Figure 3.7.

Source: From Jiang et al. [25]. Reproduced with the permission of American Chemical Society.

In the field of synthetic chemical circuits, DNA‐based logic gates played a crucial role. One interesting idea is to develop DNA circuit construction techniques and scale it up, which can help us to build larger molecular circuits systematically. In [35], starting from simple building blocks called DNA gate motif, the authors developed an abstract model for the design of large‐scale DNA circuits. The authors show that following the proposed method, circuits such as feed forward digital circuits can be effectively constructed. Stemming from this construction method, Qian and Winfree [36] presents a design of relatively complex digital logic circuits in DNA computing systems. The design is based on dual‐rail representation [18] and “seesaw” gate motif [35,36], which enables logic operations such as AND, OR, and NOT to be implemented by DNA strand displacement reactions. Such logic gates are proved cascadable, and a four‐bit square root DNA circuit is constructed as a design case to validate the scalability and computing capability of DNA logic circuits.

In 2011, an experimental method to implement neural network computation was proposed [37]. With DNA displacement reactions that implement linear threshold function, traditional computation in neural networks can be performed in molecular computing systems. A simple but interesting experiment called Hopfield associative memory validates the functionality of the system. In 2018, a more powerful DNA reaction implementation of neural network computing was provided [38]. Based on winner‐take‐all mechanism [39], computation in neural networks such as weighted summation and thresholding of binary input data can be performed in DNA reactions with high accuracy. An example of recognizing handwritten numbers from Modified National Institute of Standards and Technology (MNIST) database [40] shows that such seemingly complex computations are able to be handled by DNA strand displacement reactions. Though training in these two works is performed in silicon‐based computers, the applications show the potential of DNA materials in building scaled functional computing systems. In 2018, implementation of probabilistic switching circuits based on DNA strand displacement reactions was proposed [41]. In the fabricated system, input signals can be converted to output signals with predefined probabilities, and experiments proved the functionality of such DNA circuits.

To conclude, the designs of molecular computing systems present a design hierarchy. Starting from employing data representation methods such as fractional encoding, researchers build basic molecular circuit modules such as logic gates and clock generator. Based on that, more complex functions, e.g. DSP and neural network computation, can be realized. There are various applications in silicon‐based hardware that can be implemented by the interaction of chemical materials, which will be the main focus of future research.

This research was supported in part by NSFC under grants 61871115 and 61501116, in part by the Jiangsu Provincial NSF for Excellent Young Scholars under grant BK20180059, in part by the Six Talent Peak Program of Jiangsu Province under grant 2018‐DZXX‐001, in part by the Distinguished Perfection Professorship of Southeast University, in part by the Fundamental Research Funds for the Central Universities, and in part by the SRTP of Southeast University.

1 1 Soloveichik, D., Cook, M., Winfree, E., and Bruck, J. (2008). Nat. Comput. 7: 615–633.

2 2 Cook, M., Soloveichik, D., Winfree, E., and Bruck, J. (2009). Programmability ofchemical reaction networks. In: Algorithmic Bioprocesses, Natural Computing Series (eds. A. Condon, D. Harel, J.N. Kok, et al.), 543–584. Berlin Heidelberg: Springer.

3 3 Chen, H., Doty, D., and Soloveichik, D. (2014). Nat. Comput. 13: 517–534.

4 4 Cummings, R., Doty, D., and Soloveichik, D. (2016). Nat. Comput. 15: 245–261.

5 5 Chalk, C., Kornerup, N., Reeves, W., and Soloveichik, D. (2018). Composable rate‐independent computation in continuous chemical reaction networks. In: International Conference on Computational Methods in Systems Biology, 256–273. Springer.

6 6 Soloveichik, D., Seelig, G., and Winfree, E. (2010). Proc. Natl. Acad. Sci. U.S.A. 107: 5393–5398.

7 7 Chen, Y., Dalchau, N., Srinivas, N. et al. (2013). Nat. Nanotechnol. 8: 755–762.

8 8 Vasic, M., Soloveichik, D., and Khurshid, S. (2020). CRN++: molecular programming language. Nat. Comput. 19. Springer: 1–17.

9 9 Huang, D., Jiang, J.R., Huang, R., and Cheng, C. (2012). Compiling program control flows into biochemical reactions. In: 2012 IEEE/ACM International Conference on Computer‐Aided Design (ICCAD), 361–368.

10 10 Wang, B., Chalk, C., and Soloveichik, D. (2019). DNA: single instruction, multiple data computation with DNA strand displacement cascades. In: International Conference on DNA Computing and Molecular Programming, 219–235. Springer.

11 11 McQuarrie, D.A. (1967). J. Appl. Probab. 4: 413–478.

12 12 Shea, A., Fett, B., Riedel, M.D., and Parhi, K. (2010). Writing and compiling code into biochemistry. In: Biocomputing 2010, 456–464. World Scientific.

13 13 Murphy, N., Petersen, R., Phillips, A. et al. (2018). J. R. Soc. Interface 15: 20180283.

14 14 Thubagere, A.J., Thachuk, C., Berleant, J. et al. (2017). Nat. Commun. 8: 14373.

15 15 Beaver, D. (1995). DNA Based Comput. 27: 29–36.

16 16 Qian, L., Soloveichik, D., and Winfree, E. (2011). Efficient Turing‐universal computation with DNA polymers. In: DNA Computing and Molecular Programming (Lecture Notes in Computer Science), vol. 6518, 123–140.

17 17 Salehi, S.A., Parhi, K.K., and Riedel, M.D. (2017). Chemical reaction networks for computing polynomials. ACS Synth. Biol. 6 (1): 76–83, ACS Publications.