DNA- and RNA-Based Computing Systems

18 18 Chen, H.L., Doty, D., and Soloveichik, D. (2014). ACM Conference on Innovations in Theoretical Computer Science, 313–326.

19 19 Horn, F. and Jackson, R. (1972). Arch. Ration. Mech. Anal. 47: 81–116.

20 20 Cheng, B. and Riedel, M. (2009). Stochastic transient analysis of biochemical systems and its application to the design of biochemical logic gates. In: Biocomputing 2009, 4–14.

21 21 Jiang, H., Riedel, M.D., and Parhi, K.K. (2013). Digital logic with molecular reactions. In: 2013 IEEE/ACM International Conference on Computer‐Aided Design (ICCAD), 721–727. IEEE.

22 22 Ge, L., Zhong, Z., Wen, D. et al. (2016). IEEE Trans. Mol. Biol. Multi‐Scale Commun. 3: 33–47.

23 23 Jiang, H., Kharam, A.P., Riedel, M.D., and Parhi, K.K. (2010). A synthesis flow for digital signal processing with biomolecular reactions. In: 2010 IEEE/ACM International Conference on Computer‐Aided Design (ICCAD), 417–424. IEEE.

24 24 Jiang, H., Riedel, M.D., and Parhi, K.K. (2011). Synchronous sequential computation with molecular reactions. In: Proceedings of the 48th Design Automation Conference, 836–841.

25 25 Jiang, H., Salehi, S.A., Riedel, M., and Parhi, K.K. (2013). ACS Synth. Biol. 2: 245–254.

26 26 Kharam, A., Jiang, H., Riedel, M., and Parhi, K.K. (2011). Binary counting with chemical reactions. In: Biocomputing 2011, 302–313.

27 27 Li, M., Ge, L., You, X., and Zhang, C. (2018). Basic arithmetics based on analog signal with molecular reactions. In: 2018 IEEE International Conference on Communications (ICC), 1–6. IEEE.

28 28 Fett, B. and Riedel, M.D. (2008). Module locking in biochemical synthesis. In: 2008 IEEE/ACM International Conference on Computer‐Aided Design, 758–764. IEEE.

29 29 Salehi, S.A., Liu, X., Riedel, M.D., and Parhi, K.K. (2018). Sci. Rep. 8: 8312.

30 30 Liu, X. and Parhi, K.K. (2020). Molecular and DNA artificial neural networks via fractional coding. IEEE Trans. Biomed. Circuits Syst. 14 (3): 490–503.

31 31 Liu, X. and Parhi, K.K. (2019). Training DNA perceptrons via fractional coding. In: 2019 53rd Asilomar Conference on Signals, Systems, and Computers. IEEE.

32 32 Liu, X. and Parhi, K.K. (2019). Computing radial basis function support vector machine using DNA via fractional coding. In: Proceedings of the 56th Annual Design Automation Conference 2019, 1–6.

33 33 Salehi, S.A., Jiang, H., Riedel, M.D., and Parhi, K.K. (2015). IEEE Trans. Mol. Biol. Multi‐Scale Commun. 1: 249–264.

34 34 Salehi, S.A., Riedel, M.D., and Parhi, K.K. (2014). Asynchronous discrete‐time signal processing with molecular reactions. In: 2014 48th Asilomar conference on signals, systems and computers, 1767–1772. IEEE.

35 35 Qian, L. and Winfree, E. (2011). J. R. Soc. Interface 8: 1281–1297.

36 36 Qian, L. and Winfree, E. (2011). Science 332: 1196–1201.

37 37 Qian, L., Winfree, E., and Bruck, J. (2011). Nature 475: 368–372.

38 38 Cherry, K.M. and Qian, L. (2018). Nature 559: 370–376.

39 39 Maass, W. (2000). Neural Comput. 12: 2519–2535.

40 40 Li, D. (2012). IEEE Signal Process Mag. 29: 141–142.

41 41 Wilhelm, D., Bruck, J., and Qian, L. (2018). Proc. Natl. Acad. Sci. U.S.A. 115: 903–908.

Dmitry M. Kolpashchikov1,2* and Aresenij J. Kalnin3

1University of Central Florida, Chemistry Department, 4111 Libra Drive, Orlando, FL, 32816‐2366, USA

2University of Central Florida, Burnett School of Biomedical Sciences, 6900 Lake Nona Blvd, Orlando, FL, 32816, USA

3SCAMT Institute, Laboratory of Molecular Robotics and Biosensor Materials, 9 Lomonosova Street, St. Petersburg, 191002, Russian Federation

Electronic microprocessor systems are based on semiconductor logic gates, which employ electronic input and output signals and power supplies [1]. A critical feature, which contributes to the undoubted success of electronic circuits, is input–output signal homogeneity: the same electron voltage value emerging as an output of one gate can be admitted as an input of another gate. Such connections of logic gates can achieve selected functions of varying complexity. This very large‐scale integration is a crucial component of modern silicon processors [2,3]. The development of more powerful microprocessors depends on continued progress in miniaturizing their components. However, if current trends continue, conventional silicon chips will soon reach their physical limits [4]. Several research groups have created molecular ensembles that perform logic operations [2,3,5–9]. Even though small‐scale integration of logic elements has been achieved, there is still a lack of examples of universal large‐scale integration. Therefore, the challenges of component integration must be further addressed to advance the molecular computation field, as well as for its practical implementations [2,3].

DNA has been considered as an excellent candidate both for in vitro computation [10] and as a convenient building block for molecular switches and other devices [11–13]. Pioneered by Stojanovic [14], a great number of nucleic acid‐based logic gates of various designs have been proposed in the last 17 years [15–26]. Despite significant progress in the design of individual molecular logic gates, there is still a great challenge in solving the following technical problems: achieving high scale integration of molecular logic units, precise localization of the molecular gates in nano‐environment for efficient inter‐gate communication, and achieving reusability of DNA hardware [27–30]. Moreover, connecting the gates to an appropriate interface for convenient communication with human users is needed [31,32].

This chapter describes approaches for connecting DNA logic gates in circuits with the emphasis on (i) deoxyribozyme (Dz) logic gates, (ii) strand displacement (seesaw) logic gates, and (iii) DNA logic gates connected via four‐way junctions (4WJs). Most common problems on the way toward creating long chains of communicating DNA logic gates are discussed.

The logic gate designed by Stojanovic et al. [14] took advantage of deoxyribozymes – nonnaturally occurring DNA sequences that catalyze chemical reactions [33,34]. One of most commonly used deoxyribozyme classes in DNA‐based molecular computation is a class of RNA‐cleaving deoxyribozymes (RCDZ). The design principles for RCDZ‐based two‐input AND gate (2iAND) are shown in Figure 4.1. A DNA strand containing an RCDZ catalytic core and two substrate‐binding arms is rendered inactive by the two inactivating stems. Binding the two oligonucleotide inputs I1 and I2 to the input‐recognition loop modules unwind the inactivating stems, thus enabling binding of a fluorogenic F substrate (F sub). The cleavage of F sub results in fluorescent increase due to the separation of the fluorophore from quencher. Importantly, when added separately, I1 and I2 are unable to restore the catalytic activity of RCDZ, which ensures the appropriate logic behaviours of the 2iAND construct. NOT, OR, ANDNOT, and even three‐input ANDNOTANDNOT gates can be designed by following similar principles of RCDZ core activation and inactivation [35,36]. Splitting the RCDZ core in two halves enables designing the gates that can process up to five inputs (e.g. 5iAND gate shown in Figure 4.1b) [37]. RCDZ logic gates have been used to build complex systems including automatons that can play Tic‐Tac‐Toe game with human, which utilize over hundreds of logic gates [38,39] (reviewed in [11]).

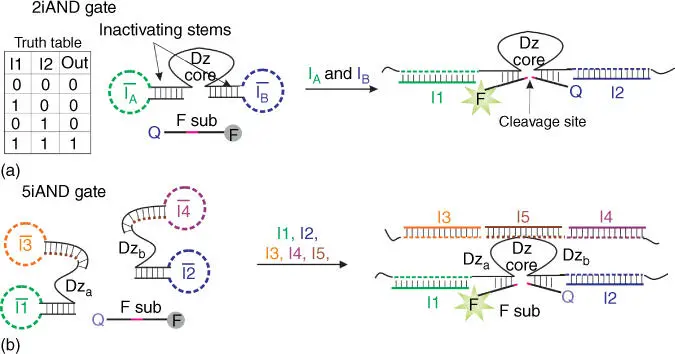
Figure 4.1Examples of deoxyribozyme‐based logic gates. (a) One of the first DNA logic gates: deoxyribozyme (Dz)‐based two‐input AND gate (2iAND)[14]. Input‐recognition modules are in green and blue. Upon hybridization of inputs I Aand I B, the substrate‐binding arms are unblocked, which restores RCDZ activity to cleave a fluorophore‐ and quencher‐labeled reporter substrate (F sub). FAM is fluorescein; Q is a dark quencher of fluorescence. (b) Dz‐based five‐input AND gate (5iAND). Dz catalytic core regains activity only when all five oligonucleotide inputs ( I1–I5) are present. I1, I2, I3, and I4open the inactivating stems, while I5bridges strands Dz aand Dz btogether to form a catalytic core [37].