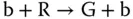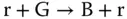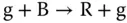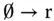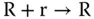After defining the various input signals in a biochemical system with one of the three types of encoding representations mentioned above, the system can be solved through ordinary differential equations (ODEs). For CRN analysis, mass action kinetics is considered as a proper kinetic scheme [19]. For mass action kinetics, the rate of a chemical reaction is proportional to the product of concentrations of reactants. For instance, consider a reaction given by
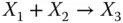
Since the reaction fires at a rate proportional to [ X 1][ X 2], or [rate of reaction] ∝ k [ X 1][ X 2], where k is rate constant associated with the reaction, we can model the reaction by ODEs as follows:
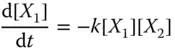
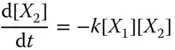
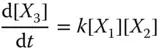
ODE simulation is a continuous deterministic model of chemical kinetics.
An alternative approach to achieving mass action kinetics modeling is referred to as stochastic simulation [20]. Compared with deterministic modeling, stochastic simulation is discrete and stochastic, and the computation is based on probabilities.
Many researchers have investigated methods to implement digital logic with molecular reactions, including combinational components and sequential components. For combinational components, the inverter is the simplest but very important logic gate since other more complicated structures such as NAND gates, adders, and multipliers will make use of it. In a biochemical system, it can be implemented by implementing the transfers between the molecular types representing 0 and 1, respectively [21]. The simplification methods for digital combinational logic have been studied in [22].
Take the AND gate as an example for two‐input logic gates implemented by molecular reactions [21]. Suppose the inputs of the gate are X and Y and the output is Z , respectively. The inputs and output signals are represented by the concentration of X 0/ X 1, Y 0/ Y 1, and Z 0/ Z 1. If the value of X is 0, then all X 1will be transferred to X 0. According to the target logic function, the chemical reactions are designed as
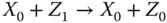
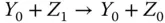
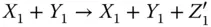
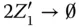
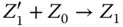
where 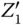 represents an indicator to generate Z 1and can be transferred to an external sink indicated by the fourth reaction. The analysis of inverter and AND gate implementation with molecular reactions can be applied to explain other complex gates such as NOR, XOR, and NAND [21], which form the basic blocks for modules like multipliers and digital signal processors.
represents an indicator to generate Z 1and can be transferred to an external sink indicated by the fourth reaction. The analysis of inverter and AND gate implementation with molecular reactions can be applied to explain other complex gates such as NOR, XOR, and NAND [21], which form the basic blocks for modules like multipliers and digital signal processors.
For sequential components, all modules are under control of the clock signals. Sequential digital logic circuits can be classified into two categories, synchronous circuits and asynchronous circuits, depending on whether the circuits are governed by a global clock or not. A sustained‐chemical‐oscillator‐based synchronization mechanism is introduced to implement synchronous circuits with molecular reactions, which have been widely studied by the synthetic biology community. An example is “red‐green‐blue” (RGB) oscillator [23–25], which is first proposed by [23] and can be used to establish an order for the transformation of molecular quantities in the counter implemented by molecular reactions. The RGB oscillator is also useful for generating a global clock as the designers wish. Reactions in an RGB oscillator are assigned to one of the three categories – red, green, and blue. Quantities are transformed between color categories according to the absence of molecules in the third category as ( Figure 3.6a)
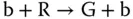
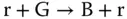
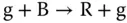
Here, R, G, and B are introduced molecular types. And r, g, and b are the “absence indicators” corresponding to R, G, and B, respectively, and are continually generated as
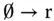
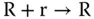
The feature of indicators quickly consumed by corresponding signal molecules assures that the succeeding phase cannot begin unless all reactions in a given phase have completed ( Figure 3.6b). With the aid of such clock signals, analog circuits for basic arithmetic, like addition, subtraction, multiplication, and division, can be implemented with molecular reactions [27].
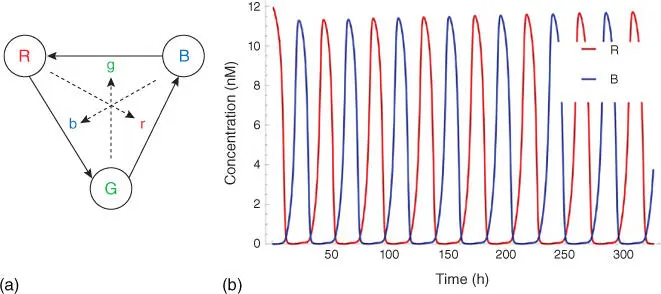
Figure 3.6(a) Sequence of reactions for the three‐phase clock based on the RGB oscillator.
Source: Adapted from Kharam et al. [26]
. (b) ODE‐based simulation of the chemical kinetics of the proposed N ‐phase clock (here N = 2), where the amplitude and frequency of oscillation waves can be adjusted.
Source: From Jiang et al. [25]. Reproduced with the permission of American Chemical Society.
Asynchronization circuits are implemented by locking the computation of biochemical modules. In asynchronous circuit designs, it is analogous to handshaking mechanisms. By introducing a specific molecular type, the module's key, to each module, the sequence of reactions is prevented from firing without the key, thus under proper control [28].
Several researchers have turned their attention to the implementation of more complicated functions in specific systems [29–32]. Salehi et al. [29] first points out that stochastic logic could be converted to molecular designs that can be readily utilized in the design of molecular filters and channel decoders. Using fractional coding [17], DNA computing‐based vector machine and artificial neural networks have been proposed in [30–32]. To resolve several complex design issues raised by nonlinear functions, Taylor series are applied to approximate a function with a polynomial [17]. A polynomial is a mathematical expression involving variables and coefficients; its operations are limited to multiplication, subtraction, addition, and nonnegative integer exponents of variables. The nucleus of designing functions with chemical reactions is to implement addition, subtraction, and multiplication with molecular reactions.
Читать дальше

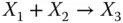
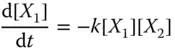
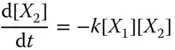
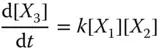
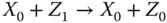
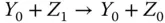
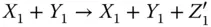
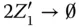
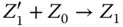
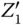 represents an indicator to generate Z 1and can be transferred to an external sink indicated by the fourth reaction. The analysis of inverter and AND gate implementation with molecular reactions can be applied to explain other complex gates such as NOR, XOR, and NAND [21], which form the basic blocks for modules like multipliers and digital signal processors.
represents an indicator to generate Z 1and can be transferred to an external sink indicated by the fourth reaction. The analysis of inverter and AND gate implementation with molecular reactions can be applied to explain other complex gates such as NOR, XOR, and NAND [21], which form the basic blocks for modules like multipliers and digital signal processors.