DNA- and RNA-Based Computing Systems

Source: From Soloveichik et al. [1]. Reproduced with the permission of Springer Nature.

With such powerful computing abilities, CRNs have the potential to build complex functional computing systems. However, it is difficult to rely on manual design when building large biocomputing systems; hence there are attempts to build corresponding compilers [8,9]. Like compilers of modern programming languages, these tools can synthesize CRNs based on a higher‐level abstraction of algorithms. Syntax of hardware description language like Verilog HDL may be used [12], where users can utilize the previously defined modules to construct their systems in a manner similar to digital hardware design. There are also attempts to synthesize CRNs from more software‐like descriptions. One critical technique is to map control flows like linear flow, branch statement, and loop statement to CRNs [9]. Another recently proposed tool [8] integrates basic arithmetic operations like additions and subtractions and is able to compile codes written in the high‐level description language called CRN++. There are some simulation results of such synthesized CRNs, showing that CRNs can well perform computation as intended. Besides synthesizing CRNs from manually written codes, by formulating the problem of CRN design (including design of reactions and related parameters) as a satisfiability modulo theory (SMT) problem and solving this problem by existing mathematical toolkits, CRNs that satisfy user specifications can be directly synthesized [13] ( Figure 3.2). Apart from CRN compilers, Thubagere et al. [14] targets the compilation of lower‐level DNA reactions. Using DNA sequences generated by the compiler, DNA circuits can be conveniently built. Since the construction of the compiler takes synthesis error into account, the experimental process can also be simplified.

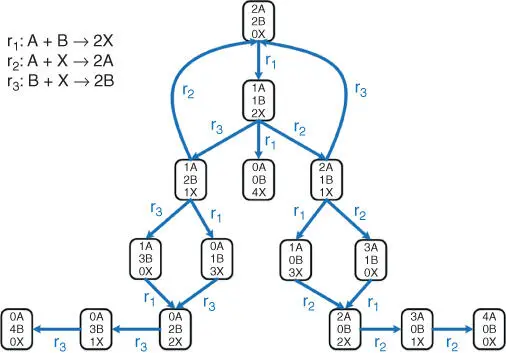
Figure 3.2State graph with state transition implemented by CRNs.

Source: Adapted from Murphy et al. [13].

To show the capability of DNA materials to establish computers, many researchers begin with building Turing machines. Apart from the aforementioned simulations of Turing machines in Figure 3.1[1], there is a universal molecular Turing machine based on site‐directed mutagenesis [15]. Qian et al. employ a “history‐free” method to implement CRNs, based on which the authors implement irreversible and reversible stack machines [16]. Besides the attempts to build Turing machines, some researchers start from the design of DNA strand displacement reactions and propose instruction sets for DNA computers. The work called SIMD||DNA (Single Instruction Multiple Data DNA) [10] leverages the cascade of DNA strand displacement reactions. By introducing a set of binary encoding rules that utilize different arrangements of upper DNA strands of DNA complexes to represent “1” and “0,” data can be stored in DNA “registers” (multistranded complexes). When adding auxiliary single DNA strands that equal to executing instructions, the upper single DNA strands can be attached/displaced/detached from the DNA complexes, hence changing the encoded data stored in DNA “registers.” An example of Rule 110 Automata is shown in Figure 3.3.

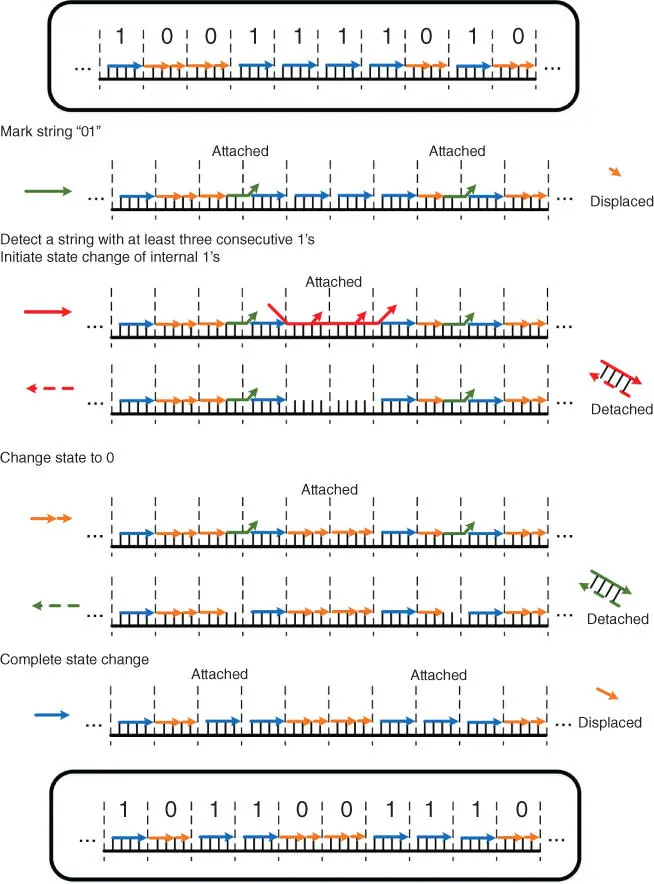
Figure 3.3Implementation of Rule 110 Automata. Two different arrangements of upper single DNA strands within each cell (slices of DNA complex separated by dashed lines) represent “1” and “0,” respectively. When executing an instruction, some specific DNA strands are added to the system to initiate the attachment, detachment, and displacement of upper DNA strands. The combination of such instructions changes the state of related cells, resulting in state transitions of the automata after the execution of all instructions.

Source: Modified from Wang et al. [10].

With the computing power of CRNs, one critical issue is how to implement such formal reactions in the real world using DNA reactions. Soloveichik et al. propose a DNA reaction substrate in [6], based on which theoretically designed reactions with less than three reactants can be readily mapped to DNA strand displacement reactions. The kinetic features of original formal reactions are approximately retained, as proved by mass action kinetic analysis. For bimolecular reactions, Qian et al. propose a design of DNA strand displacement reactions [16] to map such formal reactions. The model can address both reversible and irreversible formal reactions; unimolecular reactions and reactions with higher orders can be similarly constructed. Experimental work [7], which shows that bimolecular reactions can be mapped to DNA strand displacement reaction cascade, is based on a similar mechanism. Fluorophore experiments prove that the cascaded DNA reactions overall simulate the initial formal reactions. The diagrams of such mapping models are provided in Figure 3.4.

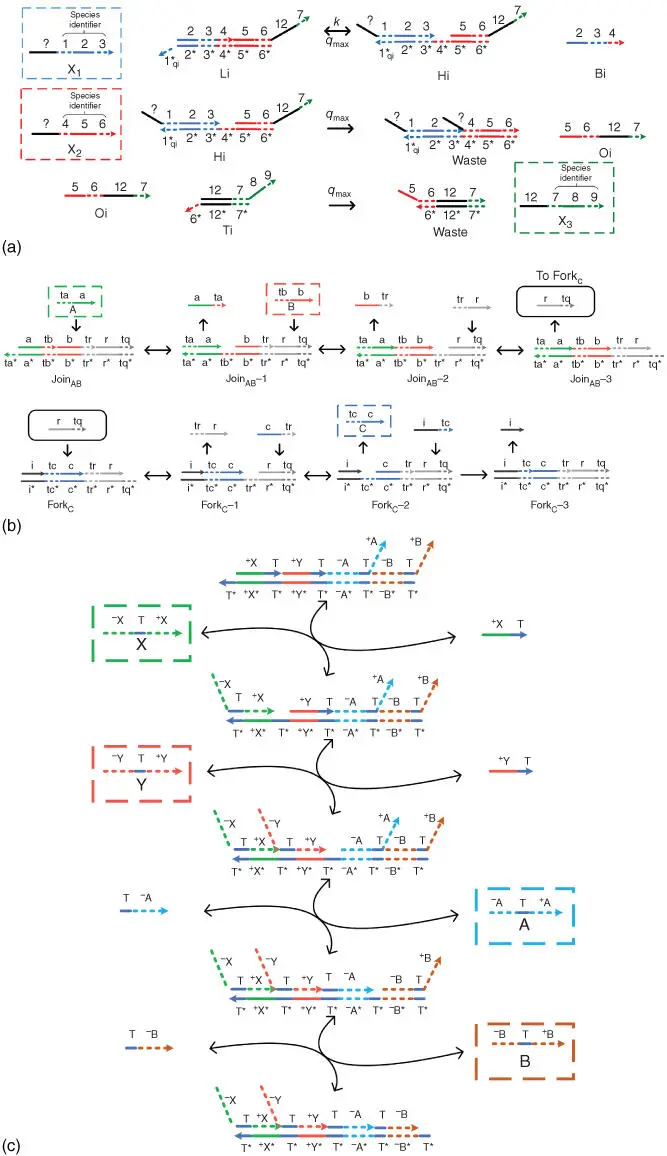
Figure 3.4Diagrams of the DNA implementation models. (a) Mapping model of bimolecular reactions in [6]. The two reactants are taken into the system using the first two reactions: one reversible and one irreversible, and the third irreversible reaction displaces the products of the formal reaction.

Source: Modified from Soloveichik et al. [6].

(b) Reaction design of A + B → C. By cascading several displacement reactions, the output is eventually displaced, and kinetic features are well reserved.

Source: Adapted from Chen et al. [7].

(c) Implementation of bimolecular reversible formal reaction.

Source: Adapted from Qian et al. [16].

In conclusion, from the perspective of theoretical computer science, chemical materials are powerful computing tools. It is capable of performing universal computing, and its programmability can be utilized by designers to create computing systems with desired functions. To fully exploit the computing power of chemical materials, there are researches focusing on the features and organization methods of CRNs and the wet experimental implementation of such systems. More applications of molecular computing are expected in future works.

In order to take advantage of the merits of DNA computing, researchers do not only use DNA computing to implement Turing machine but also try to employ it for specific applications, especially those involving complex problems. There are two basic questions arising when applying DNA computing for specific applications. One is encoding the real‐world signals to the input variables for CRNs and then decoding them back into real‐world signals after computation ( Figure 3.5). The other one is how to design chemical reactions for specific functions.

Figure 3.5The system performing encoding, computing, and decoding signals in CRNs.

Source: From Salehi et al. [17]. Reproduced with the permission of American Chemical Society.

In order to use the concentrations of molecules to represent variables' values, researchers have considered three types of encoding – the direct representation, the dual‐rail representation [18], and the fractional representation [17]. In the direct representation, values of all variables are indicated by concentrations of molecular types. In the dual‐rail representation, the difference between concentrations of two species represents the value of a variable. In the fractional representation, values of variables are determined by ratios of two molecular species in the reaction system. To be specific, e.g. if ( X 0, X 1) is the fractional representation for a variable x , its value is x = [ X 1]/([ X 0] + [ X 1]), where [·] denotes concentrations of molecular types.