DNA- and RNA-Based Computing Systems

9 9 Bell, S.A., McLean, M.E., Oh, S.K. et al. (2003). Synthesis and characterization of covalently linked single‐stranded DNA oligonucleotide‐dendron conjugates. Bioconjug Chem14 (2): 488–493.

10 10 Shagin, D.A., Shagina, I.A., Zaretsky, A.R. et al. (2017). A high‐throughput assay for quantitative measurement of PCR errors. Sci Rep7 (1): 1–11.

11 11 Ouyang, Q., Kaplan, P.D., Liu, S., and Libchaber, A. (1997). DNA solution of the maximal clique problem. Science278 (5337): 446–449.

12 12 Faulhammer, D., Cukras, A.R., Lipton, R.J., and Landweber, L.F. (2000). Molecular computation: RNA solutions to chess problems. Proc Natl Acad Sci97 (4): 1385–1389.

13 13 Chao, J., Wang, J., Wang, F. et al. (2019). Solving mazes with single‐molecule DNA navigators. Nat Mater18 (3): 273–279.

14 14 Rothemund, P.W. (2006). Folding DNA to create nanoscale shapes and patterns. Nature 440 (7082): 297–302.

15 15 Krishnan, Y. and Simmel, F.C. (2011). Nucleic acid based molecular devices. Angew Chem Int Ed50 (14): 3124–3156.

16 16 Yurke, B., Turber, A.J., Mills, A.P. Jr. et al. (2000). A DNA‐fuelled molecular machine made of DNA. Nature406: 605–608.

17 17 He, Y. and Liu, D.R. (2010). Autonomous multistep organic synthesis in a single isothermal solution mediated by a DNA walker. Nat Nanotechnol5 (11): 778–782.

18 18 Funke, J.J. and Dietz, H. (2016). Placing molecules with Bohr radius resolution using DNA origami. Nat Nanotechnol11 (1): 47–52.

19 19 Hariadi, R.F., Appukutty, A.J., and Sivaramakrishnan, S. (2016). Engineering circular gliding of actin filaments along myosin‐patterned DNA nanotube rings to study long‐term actin‐myosin behaviors. ACS Nano10 (9): 8281–8288.

20 20 Douglas, S.M., Chou, J.J., and Shih, W.M. (2007). DNA‐nanotube‐induced alignment of membrane proteins for NMR structure determination. Proc Natl Acad Sci U S A104 (16): 6644–6648.

21 21 Martin, T.G., Bharat, T.A.M., Joerger, A.C. et al. (2016). Design of a molecular support for cryo‐EM structure determination. Proc Natl Acad Sci U S A113 (47): E7456–E7463.

22 22 Shrestha, P., Jonchhe, S., Emura, T. et al. (2017). Confined space facilitates G‐quadruplex formation. Nat Nanotechnol12 (6): 582–588.

23 23 Kilchherr, F., Wachauf, C., Pelz, B. et al. (2016). Single‐molecule dissection of stacking forces in DNA. Science353 (6304): aaf5508.

24 24 Venkatesan, B.M. and Bashir, R. (2011). Nanopore sensors for nucleic acid analysis. Nat Nanotechnol6 (10): 615–624.

25 25 Bell, N.A.W., Keyser, U.F., Puchner, E.M. et al. (2014). Nanopores formed by DNA origami: a review. Fed Eur Biochem Soc588: 3564–3570.

26 26 Krishnan, S., Ziegler, D., Arnaut, V. et al. (2016). Molecular transport through large‐diameter DNA nanopores. Nat Commun7: 1–7.

27 27 Ouyang, X., Li, J., Liu, H. et al. (2013). Rolling circle amplification‐based DNA origami nanostructrures for intracellular delivery of immunostimulatory drugs. Small9 (18): 3082–3087.

28 28 Ora, A., Järvihaavisto, E., Zhang, H. et al. (2016). Cellular delivery of enzyme‐loaded DNA origami. Chem Commun52 (98): 14161–14164.

29 29 Endo, M. and Sugiyama, H. (2014). Single‐molecule imaging of dynamic motions of biomolecules in DNA origami nanostructures using high‐speed atomic force microscopy. Acc Chem Res47 (6): 1645–1653.

30 30 Rajendran, A., Endo, M., and Sugiyama, H. (2012). Single‐molecule analysis using DNA origami. Angew Chem Int Ed51 (4): 874–890.

31 31 Wang, D., Fu, Y., Yan, J. et al. (2014). Molecular logic gates on DNA origami nanostructures for microRNA diagnostics. Anal Chem86 (4): 1932–1936.

32 32 Linko, V., Nummelin, S., Aarnos, L. et al. (2016). DNA‐based enzyme reactors and systems. Nanomaterials6 (8): 139.

33 33 Fu, J., Liu, M., Liu, Y., and Yan, H. (2012). Spatially‐interactive biomolecular networks organized by nucleic acid nanostructures. Acc Chem Res45 (8): 1215–1226.

34 34 Church, G.M., Gao, Y., and Kosuri, S. (2012). Next‐generation digital information storage in DNA. Science337 (6102): 1628–1628.

35 35 Goldman, N., Bertone, P., Chen, S. et al. (2013). Toward practical high‐capacity low‐maintenance storage of digital information in synthesised DNA. Nature494 (7435): 77–80.

36 36 Blawat, M., Gaedke, K., Hütter, I. et al. (2016). Forward error correction for DNA data storage. Procedia Comput Sci80: 1011–1022.

37 37 Erlich, Y. and Zielinski, D. (2017). DNA fountain enables a robust and efficient storage architecture. Science355 (6328): 950–954.

38 38 Organick, L., Ang, S.D., Chen, Y.‐J. et al., and others (2018). Random access in large‐scale DNA data storage. Nat Biotechnol36 (3): 242.

39 39 Takahashi, C.N., Nguyen, B.H., Strauss, K., and Ceze, L. (2019). Demonstration of end‐to‐end automation of DNA data storage. Sci Rep9 (1): 1–5.

Chuan Zhang1,2

1National Mobile Communications Research Laboratory, Southeast University, Nanjing, 211189, China

2Purple Mountain Laboratories, Nanjing, 211189, China

One of the critical challenges of Moore's law is the physical limits of transistor scaling. To this end, alternative non‐silicon substitutes have been researched, among which are quantum computing, spintronic computing, and DNA computing.

Computing using DNA materials has been studied in the last few decades. Different from traditional silicon‐based computing, DNA computing is inherently massively parallel, molecular scale, and well suited for complex computing. The theoretical analysis of such computing usually builds on an abstraction model of DNA reactions, chemical reaction networks (CRNs) [1–5]. Based on such a model, there are mapping methods that can directly translate programmed CRNs to experimentally implementable DNA reactions [6,7]. Also, to enable the construction of more complex systems, compilers have also been developed [8,9]. Apart from that, some researchers also tried to establish instruction sets based on DNA reactions [10]. Overall, researchers are constructing DNA computing systems in a manner similar to constructing early computers, and more progress in this area can be expected in the near future.

CRNs have been proven a type of effective computation tool for DNA computing [1–5]. Stochastic chemical reaction networks (SCRNs) can well model the interactions among a small number of molecules [11] and are Turing‐universal [1]. The relation between the SCRN model and the conventional concepts in computer science has already been established by [2]. For both time/space bounded and unbounded computations, SCRNs are capable of simulating Turing machines with time complexity under an asymptotic upper bound and error probability under an upper bound hence are Turing‐universal. Figure 3.1shows the simulation of a register machine as an example [1]. SCRNs are also able to stably compute functions under an asymptotic upper bound of time if and only if the functions have semilinear graphs [3]. Chemical reaction computer, defined as a CRN with initial settings, is thus a powerful computation tool. Regarding the computation correctness issues, an error correction method in the construction of CRN simulation of register machines has been proposed [4]. This validates that Turing‐universal probability 1 computation (the probability of producing a correct answer is 1 as time approaches infinity) can be implemented in CRNs. A more recent work [5] addresses the composability problem in continuous CRNs. A method to construct composable CRNs is proposed to replace the error‐prone direct cascade of different CRNs.

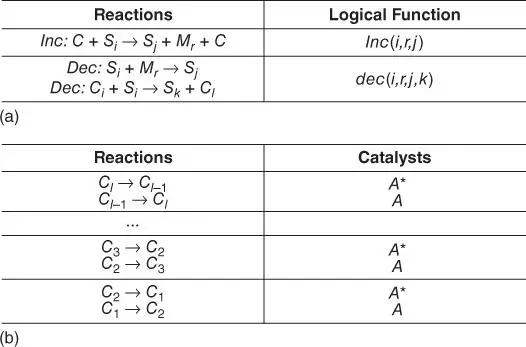
Figure 3.1The simulation of a register machine. (a) Simulation of bounded register machine. (b) Clock module used to simulate the Turing machine.