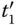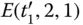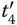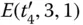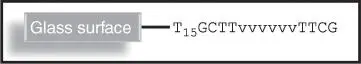DNA- and RNA-Based Computing Systems

Table 2.1The sequence of extraction operations for a given illustrative SAT problem [( x 1∨ x 2) ∧ (¬ x 2∨ x 3)].

Test tube	Operator	Values present
t 0		000, 001, 010, 011, 100, 101, 110, 111
t 1	E ( t 0, 1, 1)	100, 101, 110, 111
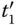	t 0− t 1	000, 001, 010, 011
t 2		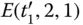010, 011
t 3	t 1+ t 2	010, 011, 100, 101, 110, 111
t 4	E ( t 3, 2, 0)	100, 101
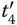	t 3− t 4	010, 011, 110, 111
t 5		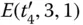011, 111
t 6	t 4+ t 5	100, 011, 101, 111

The surface‐based DNA computing model was introduced by Smith et al. [4]. In this model, DNA molecules are attached to a solid surface, instead of DNA molecules floating in a solution. Solid‐phase nucleotide synthesis is used for the immobilization of the nucleotides on the solid surface. The procedure given by Smith et al. [4] involves following six steps: (i) make, (ii) attach, (iii) mark, (iv) destroy, (v) unmark, and (vi) read out as shown in Figure 2.3.

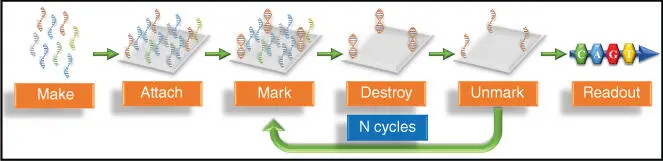
Figure 2.3Representation of surface‐based DNA computing method [4].

In this procedure, first, the sequence corresponding all possible combinations of variables is designed in step (i). To represent each combination of variables in a SAT problem, Smith et al. [4] used the DNA sequences consisting of unique DNA sequences at each end and variable DNA sequences in the middle for hybridization such as T 15GCTTvvvvvvTTCG. In this, the variable DNA sequences are represented by “vvvvvv.” The one end of these sequences has a spacer [15 “T” nucleotides (T 15)] that attaches to the surface. In step (ii), the sequences generated for all combinations are attached to the solid surface, as shown in Figure 2.4.

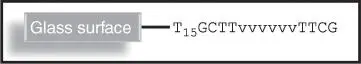
Figure 2.4Representation of surface‐bound DNA sequence.

In step (iii), the sequences corresponding to the satisfaction of each clause are marked by hybridizing these with the complementary sequences corresponding to “vvvvvv.” In step (iv), all single‐stranded sequences remaining after the hybridization are destroyed by treating with Escherichia coli Exonuclease I. In step (v), all hybridized sequences are unmarked to get the single‐stranded molecules for all the remaining surface‐bound sequences. Steps (iii)–(v) are repeated for all the clauses one after another. The unmarked sequences remaining at the end are analyzed in a readout operation using PCR in step (vi).

The procedure is explained in the context of the same illustrative SAT problem ( x 1∨ x 2) ∧ (¬ x 2∨ x 3) of three variables ( x 1, x 2, x 3) described earlier. This problem has a solution space of size 8 (each variable can be either “1,” or “0,” total solution space = 2 3). All combinations for this problem are shown in the second row ( corresponding to the test tube t 0) of Table 2.1. The problem involves two clauses: C 1= ( x 1∨ x 2) and C 2= (¬ x 2∨ x 3). The SAT is checked for these clauses one by one. C 1= ( x 1∨ x 2) is not satisfied only if x 1 x 2 x 3is represented by {000} and {001}. Therefore, the complementary sequences for all “vvvvvv” except for the above two clauses are hybridized. This eliminates the above two combinations. The remaining hybridized combinations are unmarked. Next, the SAT of C 2= (¬ x 2∨ x 3) is checked. C 2= (¬ x 2∨ x 3) is not satisfiable for {010} and {110}. Except these, all the sequences are allowed to hybridize. This leads to hybridization of {011}, {100}, {101}, and {111}. These are unmarked and identified in a readout step using PCR.

Sakamoto et al. [5] introduced a hairpin formation model for solving an SAT problem using molecular biology techniques. For a given illustrative SAT problem ( x 1∨ x 2) ∧ (¬ x 2∨ x 3), literal strings ( x 1, ¬ x 2), ( x 1, x 3), ( x 2, ¬ x 2), and ( x 2, x 3) are formed. A literal string is a string used to encode the given formula with conjunctions of the literals selected from each clause. The literal strings are obtained by concatenating of DNA sequences corresponding to each literal in a ligation step. In these literal strings, if a variable is represented in both original and negation form, then it violates the SAT condition of the given SAT problem. The literal strings without such violation in which a variable is represented only and at least in one form (either actual or negation) constitute a satisfiable solution to the given SAT problem. In Sakamoto's model, possible literal strings are first obtained by ligation. A length of the literal string equals to the number of clauses × nucleotides used for each literal. Subsequently, the obtained literal strings are subjected to temperature variation, which leads to a hairpin formation if a variable is represented in its original and negation form. The restriction enzyme destroys all such hairpins. These solutions are readily eliminated in the subsequent gel electrophoresis operation where only the literal strings with the desired length are separated. All the literal strings separated are analyzed using the sequencer, and the solution of the given SAT problem is obtained. It is to be noted that the given procedure eliminates a large number of unsatisfying literal strings, which makes it easier to deduce the correct solution from the analysis of the remaining satisfying literal strings. The procedure is useful for large size problems. However, it also has a risk of missing some literal strings due to experimental errors that may lead to an erroneous solution to the given SAT problem.

For the given illustrative SAT problem [( x 1∨ x 2) ∧ (¬ x 2∨ x 3)], a single‐stranded sequence for all literals is ligated to form the literal strings ( x 1, ¬ x 2), ( x 1, x 3), ( x 2, ¬ x 2), and ( x 2, x 3). The ligated strings are shown in Figure 2.5. These ligated strings will be subjected to restriction enzyme digestion, which eliminates the string ( x 2, ¬ x 2), and finally, the remaining literal strings are ( x 1, ¬ x 2), ( x 1, x 3), and ( x 2, x 3). From these remaining three literal strings, a solution to the given SAT problem is deduced by mathematical analysis . It is to be mentioned that only one literal string is eliminated for the given problem as it has only (2) 2[= (number of literals in each clause) number of clauses] equal to four literal strings. Though for the given illustrative example the search space is reduced only by 25% (as it removes only one literal string), for bigger problems the reduction in search space is significant. Sakamoto et al. [5] illustrated the benefit of the method by solving 6‐variable, 10‐clause problem [= ( x 1∨ x 2∨¬ x 3) ∧( x 1∨ x 3∨ x 4) ∧( x 1∨¬ x 3∨¬ x 4) ∧(¬ x 1∨¬ x 3∨ x 4) ∧( x 1∨¬ x 3∨ x 5) ∧( x 1∨ x 4∨¬ x 6) ∧(¬ x 1∨ x 3∨ x 4) ∧( x 1∨ x 3∨¬ x 4) ∧(¬ x 1∨¬ x 3∨¬ x 4) ∧(¬ x 1∨ x 3∨¬ x 4)] having three literals in each clause. This example has 3 10= 59 049 literal strings out of which only 24 literal strings were found to be satisfying the condition. Thus, ∼99.95% of the search space is eliminated using the above methodology to finally obtain the correct solution just by analyzing 24 literal strings. One of the advantages of this methodology is the use of just one step, unlike sequential elimination steps used in earlier models.