1 ...7 8 9 11 12 13 ...27 To solve the SAT problem, first, the variables are arranged in a string as x 1 x 2 x 3… x n. In Lipton's model, this variable string, x 1 x 2 x 3… x n, is represented in a graph form. Since the variables can have 0 or 1 values, the vertices with no bars (e.g. x 1, x 2, etc.) represent the 1 value, whereas those with bars (e.g. 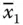 ,
, 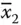 , etc.) represent 0 value. Further to aid the graphical representation, vertices a 1– a n+1are added in the sequence as a 1( x 1or
, etc.) represent 0 value. Further to aid the graphical representation, vertices a 1– a n+1are added in the sequence as a 1( x 1or 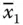 ) a 2( x 2or
) a 2( x 2or 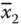 ) a 3( x 3or
) a 3( x 3or 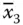 ) … a n( x nor
) … a n( x nor 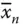 ) a n+1as shown in Figure 2.2a. It is to be noted that a 1– a n+1are the additional vertices included in the graph to commonly connect x 1and
) a n+1as shown in Figure 2.2a. It is to be noted that a 1– a n+1are the additional vertices included in the graph to commonly connect x 1and 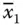 – x nand
– x nand 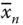 , respectively, and facilitate in representing all possible combinations for the string x 1 x 2 x 3… x n. The graphical form a 1( x 1or
, respectively, and facilitate in representing all possible combinations for the string x 1 x 2 x 3… x n. The graphical form a 1( x 1or 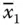 ) a 2( x 2or
) a 2( x 2or 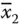 ) a 3( x 3or
) a 3( x 3or 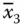 ) … a n( x nor
) … a n( x nor 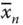 ) a n+1is represented in the DNA world by using the sequences for each vertex and edge in the same manner as that explained in Adleman's model. These DNA solutions can be amplified and separated easily based on the specific sequence represented for each variable using the biochemical steps of PCR, gel electrophoresis, and affinity separation described earlier.
) a n+1is represented in the DNA world by using the sequences for each vertex and edge in the same manner as that explained in Adleman's model. These DNA solutions can be amplified and separated easily based on the specific sequence represented for each variable using the biochemical steps of PCR, gel electrophoresis, and affinity separation described earlier.
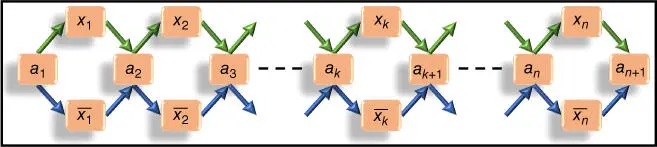
Figure 2.2Lipton's graph [3] for constructing a binary number for a general variable string ( x 1 x 2 x 3… x n).
The objective is to extract a binary sequence for x 1 x 2 x 3… x nfrom all possible combinations that satisfy all the clauses C 1, C 2, C 3, …, C m. To solve this problem, the ssDNA sequences of x 1, 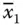 , x 2,
, x 2, 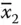 , x 3,
, x 3, 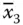 , …, x nand
, …, x nand 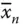 along with sequences of a 1– a n+1are added in the first test tube. Here all the sequences are selected such that the ligation represents the path between the vertices like Adleman's model. All feasible paths are represented in the first test tube. These paths are constituted by the edges from a kto both x kand
along with sequences of a 1– a n+1are added in the first test tube. Here all the sequences are selected such that the ligation represents the path between the vertices like Adleman's model. All feasible paths are represented in the first test tube. These paths are constituted by the edges from a kto both x kand 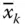 and from both x kand
and from both x kand 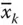 to a k+1for any k th variable. If the vertex takes the x klabel, it encodes the value “1,” and if it takes the
to a k+1for any k th variable. If the vertex takes the x klabel, it encodes the value “1,” and if it takes the 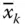 label, it encodes the value “0.” For example, the path a 1
label, it encodes the value “0.” For example, the path a 1 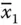 a 2 x 2a 3 x 3a 4encodes binary number 011. The next operation is the extraction in which the solution that satisfies the Boolean formula has to be extracted from all feasible solutions present in the first test tube. For this, the DNA solutions are operated by an extraction operator E ( t , i , v ) in several sequential steps in which t represents the sequences of the tube where an i th bit of variable string x 1 x 2 x 3… x nis equal to v {0, 1}. Here the extraction operator E ( t , i , v ) is selected sequentially such that clauses C 1, C 2, C 3, …., C mare satisfied one after another. Thus, the first extraction operation is selected to make C 1satisfiable. All DNA solutions satisfying C 1are then subjected to the next extraction operation, which makes C 2satisfiable and so on. If any solution is left in the tube after sequentially satisfying C 1, C 2, C 3, …., C mclauses, then it implies that the given Boolean formula is satisfiable for the sequence remained in the tube. If no solution is left, then it implies that the given Boolean formula is not satisfiable.
a 2 x 2a 3 x 3a 4encodes binary number 011. The next operation is the extraction in which the solution that satisfies the Boolean formula has to be extracted from all feasible solutions present in the first test tube. For this, the DNA solutions are operated by an extraction operator E ( t , i , v ) in several sequential steps in which t represents the sequences of the tube where an i th bit of variable string x 1 x 2 x 3… x nis equal to v {0, 1}. Here the extraction operator E ( t , i , v ) is selected sequentially such that clauses C 1, C 2, C 3, …., C mare satisfied one after another. Thus, the first extraction operation is selected to make C 1satisfiable. All DNA solutions satisfying C 1are then subjected to the next extraction operation, which makes C 2satisfiable and so on. If any solution is left in the tube after sequentially satisfying C 1, C 2, C 3, …., C mclauses, then it implies that the given Boolean formula is satisfiable for the sequence remained in the tube. If no solution is left, then it implies that the given Boolean formula is not satisfiable.
Consider a simple example of ( x 1∨ x 2) ∧ (¬ x 2∨ x 3) for illustration. In this formula, variables x 1, x 2, and x 3are present. The objective is to find a binary string for x 1 x 2 x 3, which satisfies the clauses C 1= ( x 1∨ x 2) and C 2= (¬ x 2∨ x 3). Boolean formula ( x 1∨ x 2) ∧ (¬ x 2∨ x 3) will be solved by making the test tubes for all possibilities, as given in Table 2.1. There are three variables, x 1, x 2, and x 3, represented by “0” or “1,” which leads to total eight possibilities (2 3= 8). These eight possible ways are encoded in the form of DNA molecules just by pouring all individual sequences of vertices and edges into the test tube t 0and performing the ligation. Next, the extraction operation is performed on this tube t 0. The first extraction operator is E ( t 0, 1, 1), which extract values having the first bit as “1” since this makes first clause C 1= ( x 1∨ x 2) true. Also, the second bit corresponding to x 2can make C 1= ( x 1∨ x 2) true. Therefore, all remaining solutions that do not satisfy the E ( t 0, 1, 1) are extracted in the tube t 1′. These solutions from t 1′ are then subjected to the second condition where x 2becomes 1. Thus, the next extraction operation, t 2, is 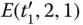 . The solutions extracted by t 1and t 2represent the solutions that satisfy C 1= ( x 1∨ x 2). These solutions are stored in tube t 3and subjected to the next extraction operation, which makes C 2= (¬ x 2∨ x 3) satisfiable. In the next operation, E ( t 3, 2, 0) is performed to extract the solution having ¬ x 2equal to 1, which satisfies C 2= (¬ x 2∨ x 3). Further, the SAT of C 2= (¬ x 2∨ x 3) depends on x 3. Therefore, all the remaining solutions stored in
. The solutions extracted by t 1and t 2represent the solutions that satisfy C 1= ( x 1∨ x 2). These solutions are stored in tube t 3and subjected to the next extraction operation, which makes C 2= (¬ x 2∨ x 3) satisfiable. In the next operation, E ( t 3, 2, 0) is performed to extract the solution having ¬ x 2equal to 1, which satisfies C 2= (¬ x 2∨ x 3). Further, the SAT of C 2= (¬ x 2∨ x 3) depends on x 3. Therefore, all the remaining solutions stored in 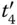 are subjected to
are subjected to 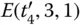 . This extracts the solutions having x 3equal to 1. These extracted solutions are stored in t 5. Finally, the solutions left in t 4and t 5are the solutions that make the given Boolean formula satisfiable. Similarly, the sequence of extraction steps for evaluating the SAT of any Boolean formula can be designed efficiently, as illustrated in the above example.
. This extracts the solutions having x 3equal to 1. These extracted solutions are stored in t 5. Finally, the solutions left in t 4and t 5are the solutions that make the given Boolean formula satisfiable. Similarly, the sequence of extraction steps for evaluating the SAT of any Boolean formula can be designed efficiently, as illustrated in the above example.
Читать дальше

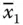 ,
, 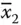 , etc.) represent 0 value. Further to aid the graphical representation, vertices a 1– a n+1are added in the sequence as a 1( x 1or
, etc.) represent 0 value. Further to aid the graphical representation, vertices a 1– a n+1are added in the sequence as a 1( x 1or 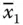 ) a 2( x 2or
) a 2( x 2or 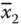 ) a 3( x 3or
) a 3( x 3or 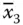 ) … a n( x nor
) … a n( x nor 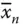 ) a n+1as shown in Figure 2.2a. It is to be noted that a 1– a n+1are the additional vertices included in the graph to commonly connect x 1and
) a n+1as shown in Figure 2.2a. It is to be noted that a 1– a n+1are the additional vertices included in the graph to commonly connect x 1and 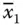 – x nand
– x nand 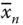 , respectively, and facilitate in representing all possible combinations for the string x 1 x 2 x 3… x n. The graphical form a 1( x 1or
, respectively, and facilitate in representing all possible combinations for the string x 1 x 2 x 3… x n. The graphical form a 1( x 1or 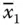 ) a 2( x 2or
) a 2( x 2or 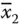 ) a 3( x 3or
) a 3( x 3or 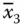 ) … a n( x nor
) … a n( x nor 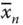 ) a n+1is represented in the DNA world by using the sequences for each vertex and edge in the same manner as that explained in Adleman's model. These DNA solutions can be amplified and separated easily based on the specific sequence represented for each variable using the biochemical steps of PCR, gel electrophoresis, and affinity separation described earlier.
) a n+1is represented in the DNA world by using the sequences for each vertex and edge in the same manner as that explained in Adleman's model. These DNA solutions can be amplified and separated easily based on the specific sequence represented for each variable using the biochemical steps of PCR, gel electrophoresis, and affinity separation described earlier.
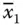 , x 2,
, x 2, 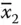 , x 3,
, x 3, 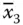 , …, x nand
, …, x nand 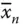 along with sequences of a 1– a n+1are added in the first test tube. Here all the sequences are selected such that the ligation represents the path between the vertices like Adleman's model. All feasible paths are represented in the first test tube. These paths are constituted by the edges from a kto both x kand
along with sequences of a 1– a n+1are added in the first test tube. Here all the sequences are selected such that the ligation represents the path between the vertices like Adleman's model. All feasible paths are represented in the first test tube. These paths are constituted by the edges from a kto both x kand 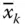 and from both x kand
and from both x kand 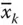 to a k+1for any k th variable. If the vertex takes the x klabel, it encodes the value “1,” and if it takes the
to a k+1for any k th variable. If the vertex takes the x klabel, it encodes the value “1,” and if it takes the 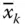 label, it encodes the value “0.” For example, the path a 1
label, it encodes the value “0.” For example, the path a 1 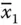 a 2 x 2a 3 x 3a 4encodes binary number 011. The next operation is the extraction in which the solution that satisfies the Boolean formula has to be extracted from all feasible solutions present in the first test tube. For this, the DNA solutions are operated by an extraction operator E ( t , i , v ) in several sequential steps in which t represents the sequences of the tube where an i th bit of variable string x 1 x 2 x 3… x nis equal to v {0, 1}. Here the extraction operator E ( t , i , v ) is selected sequentially such that clauses C 1, C 2, C 3, …., C mare satisfied one after another. Thus, the first extraction operation is selected to make C 1satisfiable. All DNA solutions satisfying C 1are then subjected to the next extraction operation, which makes C 2satisfiable and so on. If any solution is left in the tube after sequentially satisfying C 1, C 2, C 3, …., C mclauses, then it implies that the given Boolean formula is satisfiable for the sequence remained in the tube. If no solution is left, then it implies that the given Boolean formula is not satisfiable.
a 2 x 2a 3 x 3a 4encodes binary number 011. The next operation is the extraction in which the solution that satisfies the Boolean formula has to be extracted from all feasible solutions present in the first test tube. For this, the DNA solutions are operated by an extraction operator E ( t , i , v ) in several sequential steps in which t represents the sequences of the tube where an i th bit of variable string x 1 x 2 x 3… x nis equal to v {0, 1}. Here the extraction operator E ( t , i , v ) is selected sequentially such that clauses C 1, C 2, C 3, …., C mare satisfied one after another. Thus, the first extraction operation is selected to make C 1satisfiable. All DNA solutions satisfying C 1are then subjected to the next extraction operation, which makes C 2satisfiable and so on. If any solution is left in the tube after sequentially satisfying C 1, C 2, C 3, …., C mclauses, then it implies that the given Boolean formula is satisfiable for the sequence remained in the tube. If no solution is left, then it implies that the given Boolean formula is not satisfiable.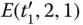 . The solutions extracted by t 1and t 2represent the solutions that satisfy C 1= ( x 1∨ x 2). These solutions are stored in tube t 3and subjected to the next extraction operation, which makes C 2= (¬ x 2∨ x 3) satisfiable. In the next operation, E ( t 3, 2, 0) is performed to extract the solution having ¬ x 2equal to 1, which satisfies C 2= (¬ x 2∨ x 3). Further, the SAT of C 2= (¬ x 2∨ x 3) depends on x 3. Therefore, all the remaining solutions stored in
. The solutions extracted by t 1and t 2represent the solutions that satisfy C 1= ( x 1∨ x 2). These solutions are stored in tube t 3and subjected to the next extraction operation, which makes C 2= (¬ x 2∨ x 3) satisfiable. In the next operation, E ( t 3, 2, 0) is performed to extract the solution having ¬ x 2equal to 1, which satisfies C 2= (¬ x 2∨ x 3). Further, the SAT of C 2= (¬ x 2∨ x 3) depends on x 3. Therefore, all the remaining solutions stored in 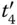 are subjected to
are subjected to 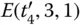 . This extracts the solutions having x 3equal to 1. These extracted solutions are stored in t 5. Finally, the solutions left in t 4and t 5are the solutions that make the given Boolean formula satisfiable. Similarly, the sequence of extraction steps for evaluating the SAT of any Boolean formula can be designed efficiently, as illustrated in the above example.
. This extracts the solutions having x 3equal to 1. These extracted solutions are stored in t 5. Finally, the solutions left in t 4and t 5are the solutions that make the given Boolean formula satisfiable. Similarly, the sequence of extraction steps for evaluating the SAT of any Boolean formula can be designed efficiently, as illustrated in the above example.










