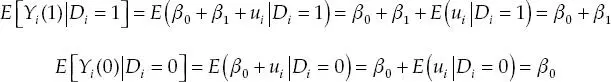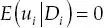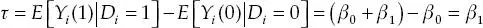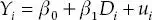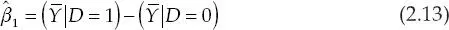
que coincide precisamente con la definición del 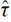 ATT provisto en la ecuación (2.10).
ATT provisto en la ecuación (2.10).
Éste se conoce como el supuesto de independencia condicional e indica que conocer Di no añade ninguna información adicional acerca de ui . En otras palabras, los individuos que participan en el programa no son sistemáticamente distintos de los individuos que no participan en el programa en características contenidas en ui .
Bajo el supuesto (2.12), el estimador de β 1por el método de mínimos cuadrados ordinarios (MCO)14 es consistente e insesgado.15 Lo primero implica que el estimador de β 1por MCO, 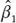 , converge en probabilidad a β 1, es decir, el límite del estimador a medida que aumenta el tamaño de muestra es exactamente el parámetro que se va a estimar. Lo segundo significa que el valor esperado del estimador de MCO es igual al valor del parámetro, es decir, , independientemente del tamaño de la muestra.
, converge en probabilidad a β 1, es decir, el límite del estimador a medida que aumenta el tamaño de muestra es exactamente el parámetro que se va a estimar. Lo segundo significa que el valor esperado del estimador de MCO es igual al valor del parámetro, es decir, , independientemente del tamaño de la muestra.
El parámetro β 1en la ecuación (2.11) se interpreta como el efecto del programa o la diferencia de medias de la variable de resultado entre el grupo de tratamiento y el grupo de control. Note que tomando expectativa condicional en la ecuación (2.11) se obtiene:
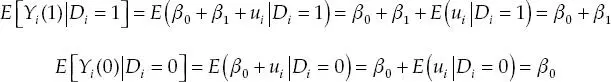
porque 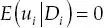
Entonces
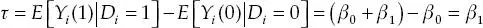
El estimador de MCO de β 1estaría dado por:16
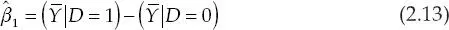
que coincide precisamente con la definición del 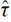 ATT provisto en la ecuación (2.10).
ATT provisto en la ecuación (2.10).
Ejemplo 2.1:
Suponga que debemos evaluar el impacto del programa Canasta, que es un programa de nutrición dirigido a niños entre los 0 y 6 años de edad. El programa consiste en la provisión de un mercado por valor de $X al mes a las madres participantes de niños en el rango de edad elegible. La composición del mercado es revisada por nutricionistas expertos para asegurarse de que la ingesta diaria por nutriente sea la adecuada, dada la edad de los niños beneficiarios. El programa está dirigido a familias de Sisbén 17 1 y 2.
El indicador de participación en el programa se define como:

Los niños de familias de Sisbén 1 y 2 entre los 0 y 6 años de edad que participan en el programa constituyen el grupo de tratamiento, mientras que los niños de familias de Sisbén 1 y 2 entre los 0 y 6 años de edad que no participan en el programa son el grupo de control. Como variable de resultado, Yi , se identifica el puntaje Z ( Z-score ) de estatura según la edad. El puntaje Z corresponde a la estatura del niño estandarizada de acuerdo con las medias y varianzas poblacionales, según grupos de edad y sexo. El puntaje Z de estatura según la edad resulta de restarle a la estatura del niño la media poblacional de estatura para su grupo de edad y sexo, y dividir esta diferencia por la desviación estándar de la estatura de su grupo de edad y sexo en la población. El resultado indica el número de desviaciones estándar que el niño está por encima (o por debajo) de su media poblacional. Un puntaje Z de cero indica que el niño se ubica exactamente en la media de su grupo.
E [ Y i(1)| D i= 1] es en este caso el promedio del puntaje Z de estatura en el grupo de tratamiento en presencia del programa. E [ Y i(0)| D i= 1] es el promedio del puntaje Z de estatura en el grupo de tratamiento en ausencia del programa. Es decir, cuál habría sido el promedio del puntaje Z de estatura según la edad en el escenario hipotético de que el programa no hubiera existido. Este contrafactual no se observa, y esto constituye la principal dificultad de la evaluación de impacto.
E [ Y i(0)| D i= 0] es el promedio del puntaje Z de estatura en el grupo de niños no participantes (o grupo de control).
Suponga que la variable de resultado en que estamos interesados es la incidencia de desnutrición crónica, es decir, la probabilidad de que la estatura del niño esté dos desviaciones estándar por debajo de lo que debería estar, dados su edad y su sexo (es decir, que el puntaje Z de estatura según la edad sea menor que –2). En este caso E [ Y i(1)| D i= 1] sería el porcentaje de niños participantes con desnutrición crónica en presencia del programa.
Si sucediera que los promedios del puntaje Z de estatura en el grupo de tratamiento y en el grupo de control son idénticos en ausencia del programa (es decir, se cumpliera el supuesto (2.8)), entonces el efecto del programa se podría estimar simplemente comparando la media de la variable de resultado en el grupo de tratamiento con la media de la variable de resultado en el grupo de control. Esto se puede implementar con una regresión lineal del puntaje Z de estatura según la edad ( Yi ) sobre la variable binaria de participación, Di , estimada por MCO:
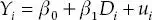
β 1sería el efecto del programa de nutrición sobre el indicador antropométrico escogido si se cumple el supuesto de independencia condicional (2.12).
En este capítulo hemos asumido que el investigador sabe exactamente cuál es la variable de resultado Y que quiere medir y tiene los datos a disposición. En general, la elección de una variable de resultado Y con base en la cual se determinará la efectividad de un programa no es una pregunta trivial. La elección de Y debe estar guiada principalmente por los objetivos y lineamientos del programa que se evalúa. Por ejemplo, el programa Canasta es un programa cuyo objetivo es mejorar el estado nutricional de los niños beneficiarios, con base en la provisión de un mercado que contiene un porcentaje de los requerimientos nutricionales diarios. Por tanto, es razonable que la variable de resultado seleccionada sea un indicador del estado nutricional de los niños (estatura según la edad, peso según la edad, o estatura según el peso). Existen casos como éste en que la escogencia de la variable de resultado es relativamente obvia, pero otros casos en los que no es elemental.
Читать дальше

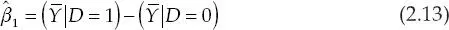
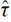 ATT provisto en la ecuación (2.10).
ATT provisto en la ecuación (2.10).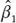 , converge en probabilidad a β 1, es decir, el límite del estimador a medida que aumenta el tamaño de muestra es exactamente el parámetro que se va a estimar. Lo segundo significa que el valor esperado del estimador de MCO es igual al valor del parámetro, es decir, , independientemente del tamaño de la muestra.
, converge en probabilidad a β 1, es decir, el límite del estimador a medida que aumenta el tamaño de muestra es exactamente el parámetro que se va a estimar. Lo segundo significa que el valor esperado del estimador de MCO es igual al valor del parámetro, es decir, , independientemente del tamaño de la muestra.