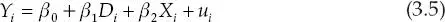
donde Xi es una característica observable del individuo, que explica tanto la participación en el programa como la variable de resultado Yi .
Por ejemplo, si los individuos más pobres son aquellos que deciden participar en el programa Canasta, mientras que los individuos más ricos eligen no hacerlo, entonces Xi sería el índice de riqueza del hogar. Si esta es la única diferencia entre los participantes y los no participantes, entonces el estimador de β 1en la ecuación (3.5) por MCO es un estimador consistente e insesgado del efecto del programa.
Si las diferencias entre los participantes y no participantes son todas observables (y la base de datos contiene información acerca de todas ellas), entonces la regresión (3.5) se puede extender para incluir todas esas características. Si todas las diferencias entre el grupo de tratamiento y el grupo de control se incluyen en la regresión, entonces los factores restantes contenidos en ui son efectivamente independientes de la decisión de participar, Di , y, por ende, el estimador de β 1por MCO es un estimador insesgado y consistente del efecto del programa.
Sin embargo, en la mayoría de los casos, algunas de las diferencias entre los participantes y los no participantes no se observan o son características (en principio observables) que no están contenidas en la base de datos. 20 Por ejemplo, las madres más dedicadas a sus hijos pueden ser más propensas a participar en el programa Canasta que las madres menos dedicadas. Pero qué tan dedicada es una madre no es una variable incluida en las encuestas. Por ende, aunque sabemos que ésta es una diferencia entre los beneficiarios y los no beneficiarios por la que debemos controlar en la ecuación (3.5), no tenemos los datos a disposición. En este caso, el estimador de MCO de β 1está sesgado , es decir:
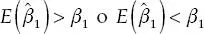
La dirección precisa del sesgo (llamado sesgo de selección, por las razones que se han expuesto anteriormente) depende de la relación existente entre la participación en el programa y la variable que diferencia a los participantes de los no participantes (llamémosla W ), y de la dirección del efecto de la variable excluida W sobre la variable de resultado Y .
Teniendo en mente el siguiente modelo:
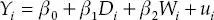
donde W es una característica no observable (o no contenida en la encuesta), la dirección del sesgo de 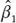 por MCO sobre la regresión (3.5) se puede resumir de la siguiente manera:
por MCO sobre la regresión (3.5) se puede resumir de la siguiente manera:

donde Corr ( Di, Wi ) es la correlación entre Di y Wi .
Por ejemplo, tomemos el caso de la primera celda (superior-izquierda). Si a mayor dedicación de la madre (variable W no observada), mayor es la probabilidad de participar en el programa Canasta, entonces Corr ( Di, Wi ) > 0. Si, además, la dedicación de la madre aumenta la estatura según la edad del niño (variable de resultado Yi ) porque la dieta que ofrece la madre más dedicada es más balanceada, entonces β 2> 0. En este caso, el estimador de MCO de 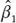 en la regresión (3.4) estaría sesgado hacia arriba E (
en la regresión (3.4) estaría sesgado hacia arriba E ( 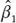 ) > β 1, es decir, el efecto estimado del programa sobre el peso según la estatura es mayor que el efecto verdadero del programa. Esto se presenta porque, al no poder incluir W en la regresión, le estamos atribuyendo al programa (a Di ) parte del efecto positivo que tiene W sobre Y . Es decir, se le atribuye al programa parte del efecto positivo de la mayor motivación de las madres participantes sobre el estado nutricional de sus hijos. En otras palabras, Di absorbe tanto su efecto propio (sobre Y ) como el efecto que tiene W directamente sobre Y, dando lugar a un efecto más grande de lo que en realidad es.
) > β 1, es decir, el efecto estimado del programa sobre el peso según la estatura es mayor que el efecto verdadero del programa. Esto se presenta porque, al no poder incluir W en la regresión, le estamos atribuyendo al programa (a Di ) parte del efecto positivo que tiene W sobre Y . Es decir, se le atribuye al programa parte del efecto positivo de la mayor motivación de las madres participantes sobre el estado nutricional de sus hijos. En otras palabras, Di absorbe tanto su efecto propio (sobre Y ) como el efecto que tiene W directamente sobre Y, dando lugar a un efecto más grande de lo que en realidad es.
La gran mayoría de programas que se evalúan en la actualidad están caracterizados por el hecho de que los individuos deben elegir si participan o no. Esto implica que las diferencias que surgen entre los participantes y no participantes son, en buena parte, no observables. Así, el gran reto de la evaluación de impacto es encontrar metodologías que permitan obtener un estimador consistente e insesgado de β 1aun en presencia del sesgo de selección. Estas diversas metodologías se discuten en los capítulos a continuación.
Blundell, R. y M. Costa Dias, 2009, “Alternative Approaches to Evaluation in Empirical Microeconomics,” Journal of Human Resources , University of Wisconsin Press, vol. 44(3), 565-640.
Heckman, J., R. LaLonde y J. Smith, 1999, “The Economics and Econometrics of Active Labor Market Programs,” en O. Ashenfelter y D. Card, capítulo 31, Handbook of Labor Economics , Vol. IV, 1865-2073.
Smith, J., 2000, “A Critical survey of Empirical Methods for Evaluating Active Labor Market Policies”, Schweizerische Zeitschrift fr Volkswirthschaft und Statistik , 136(6), 1-22.
Stock, J. y M. Watson, 2006, Introduction to Econometrics . Segunda edición. Boston, MA.: Addison-Wesley, Series in Economics.
18Esto en contraste con la participación asignada de manera aleatoria, como se estudiará en el capítulo 4 sobre experimentos aleatorios controlados.
19Esto se debe a que para demostrar que el estimador de MCO es insesgado se requiere que se cumpla el supuesto E ( ui | Di ) = 0. Ver el anexo 2.
20Es posible también que el investigador omita del análisis una variable que sí está registrada en la base de datos por descuido o desconocimiento.
PARTE II
EXPERIMENTOS SOCIALES CONTROLADOS Y EXPERIMENTOS NATURALES
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

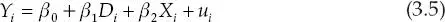
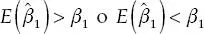
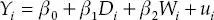
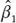 por MCO sobre la regresión (3.5) se puede resumir de la siguiente manera:
por MCO sobre la regresión (3.5) se puede resumir de la siguiente manera:











