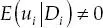Recuerde que el  ATT se puede escribir como:
ATT se puede escribir como:
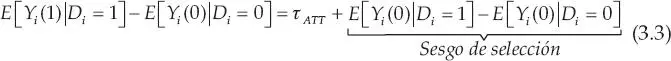
En la ecuación (3.3) es claro que si los individuos del grupo de tratamiento y el grupo de control son diferentes, aun en ausencia del tratamiento (la segunda parte al lado derecho de la ecuación), entonces la diferencia entre la media del grupo de tratamiento y la media del grupo de control (el lado izquierdo de la ecuación) será igual al  ATT más la diferencia preexistente entre los dos grupos, término que se denomina sesgo de selección. Es decir, la comparación de medias entre el grupo de tratamiento y el grupo de control será una combinación del efecto directo del tratamiento,
ATT más la diferencia preexistente entre los dos grupos, término que se denomina sesgo de selección. Es decir, la comparación de medias entre el grupo de tratamiento y el grupo de control será una combinación del efecto directo del tratamiento,  ATT , y las diferencias preexistentes entre los dos grupos, E [ Yi (0)| Di = 1] = E [ Yi (0)| Di = 0], y sin información adicional el investigador no puede descifrar qué parte se debe a qué.
ATT , y las diferencias preexistentes entre los dos grupos, E [ Yi (0)| Di = 1] = E [ Yi (0)| Di = 0], y sin información adicional el investigador no puede descifrar qué parte se debe a qué.
En suma, los individuos que se autoseleccionan en el grupo de tratamiento son sistemáticamente diferentes (en formas que observamos y formas que no observamos) de los individuos que se autoseleccionan en el grupo de control, y precisamente por eso participan en el programa. Esas diferencias sistemáticas pueden estar relacionadas, a su vez, con la variable de resultado, objeto de la evaluación de impacto.
En el capítulo anterior se explicó que si se cumple el supuesto (3.2), entonces el efecto del programa sobre la variable de resultado, Yi , es la pendiente estimada por mínimos cuadrados ordinarios de la siguiente regresión lineal:

donde Di es el indicador del estatus de tratamiento.
En este caso, 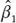 por MCO es un estimador consistente e insesgado del efecto del programa porque E ( ui | Di ) = 0. Es decir, no hay correlación entre la decisión de participar o no en el programa, Di , y las características observadas y no observadas de los individuos contenidas en el término de error, ui . Sin embargo, si la participación en el programa es una decisión de los individuos, 18 es improbable que se cumpla el supuesto E ( ui | Di ) = 0. Esto se presenta porque es posible que los individuos que deciden participar en el programa lo hagan debido a que son sistemáticamente diferentes de los individuos que deciden no participar. Algunas de estas diferencias pueden, a su vez, explicar la variable de resultado, Yi , y, por tanto, estar contenidas en el término de error, ui . Dicho de otra manera, saber si un individuo participa o no participa en el programa informa sobre las variables no observadas del individuo contenidas en ui , por lo cual se invalida el supuesto de independencia condicional.
por MCO es un estimador consistente e insesgado del efecto del programa porque E ( ui | Di ) = 0. Es decir, no hay correlación entre la decisión de participar o no en el programa, Di , y las características observadas y no observadas de los individuos contenidas en el término de error, ui . Sin embargo, si la participación en el programa es una decisión de los individuos, 18 es improbable que se cumpla el supuesto E ( ui | Di ) = 0. Esto se presenta porque es posible que los individuos que deciden participar en el programa lo hagan debido a que son sistemáticamente diferentes de los individuos que deciden no participar. Algunas de estas diferencias pueden, a su vez, explicar la variable de resultado, Yi , y, por tanto, estar contenidas en el término de error, ui . Dicho de otra manera, saber si un individuo participa o no participa en el programa informa sobre las variables no observadas del individuo contenidas en ui , por lo cual se invalida el supuesto de independencia condicional.
Ejemplo 3.1:
Suponga que el programa Canasta se ofrece y los individuos elegibles deben decidir si quieren participar o no. Además, participar tiene un costo en tiempo y trámites, debido a que la mamá del niño elegible debe acercarse a una oficina de la institución encargada de administrar el programa, diligenciar un formulario de inscripción y llevar al niño potencialmente participante a un control médico en el que se registran sus medidas antropométricas (estatura y peso). Aunque todas las mamás de niños entre los 0 y 6 años de edad que pertenecen a Sisbén 1 y 2 son elegibles para el programa, es muy probable que un conjunto de madres considere que el costo de inscribirse para participar en el programa es muy alto porque las filas son muy largas, el examen médico es muy demorado o el hospital en el que se lleva a cabo es muy lejos, por lo cual preferirán no recibir el mercado. Es decir, se podría pensar que las mamás que sí deciden participar son aquellas más proactivas y motivadas y que, a pesar del costo de participación, se preocupan por sus hijos y su bienestar lo suficiente (o tienen el tiempo disponible) como para ir hasta la oficina, hacer la fila, sacar la cita en el hospital, ir al hospital para asistir a la cita médica, volver a la oficina administradora a reclamar el mercado, etcétera.
Note entonces que las madres participantes y las madres no participantes son diferentes en cuanto a su perfil de madre, la disponibilidad de tiempo, su disposición a ocuparse de los hijos, etc. Estas características, algunas de las cuales no son observadas por el evaluador porque no existen mediciones o porque no fueron registradas en los datos (como qué tan dedicada es la mamá a sus hijos), pueden también afectar el estado nutricional de los niños participantes y no participantes. Por ejemplo, las mamás más proactivas y motivadas pueden ser también aquellas que se preocupan más por la nutrición de los niños y, por tanto, les ofrecen una dieta más balanceada, llevan a los niños a controles médicos, etc. Es decir, sería una variable contenida en ui porque explica la medida antropométrica (o variable de resultado), Yi .
Dado que existen características observadas y no observadas de los individuos, contenidas en ui , que explican tanto la decisión de participar en el programa como la variable de resultado, entonces
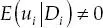
Es decir, la participación en el programa, Di , sí está correlacionada con el término de error en la regresión (3.4). Esto constituye la violación de uno de los supuestos fundamentales del modelo de regresión lineal (independencia condicional) y, por ende, los estimadores de mínimos cuadrados ordinarios no serán insesgados. 19 Esto implica que el valor esperado del estimador del efecto del programa estimado por MCO no corresponde al efecto verdadero del programa sino que está subestimado o sobrestimado, según sean las características no observadas de los individuos. En otras palabras, el efecto del programa no se puede obtener por la simple comparación de medias de la variable de resultado entre el grupo de tratamiento y el grupo de control.
Intuitivamente, si hay variables que explican tanto la participación en el programa como la variable de resultado, la comparación de medias puede estar atribuyendo al programa un efecto que en realidad se debe a las diferencias preexistentes entre el grupo de tratamiento y el grupo de control. En nuestro ejemplo del programa Canasta, si las madres participantes son más dedicadas y están más motivadas que las madres no participantes, entonces podemos estar atribuyendo al programa un efecto positivo sobre el estado nutricional de los niños, cuando en realidad la diferencia en las medidas antropométricas a favor de los niños tratados se debe a que tienen madres más pendientes de su dieta que los niños de control, y no al programa en sí. Si la característica del individuo, Xi , que explica tanto la participación en el programa como la variable de resultado, es observable y está contenida en la base de datos disponible, entonces este problema se soluciona simplemente incluyéndola en la regresión (3.4) como una variable explicativa adicional:
Читать дальше

 ATT se puede escribir como:
ATT se puede escribir como: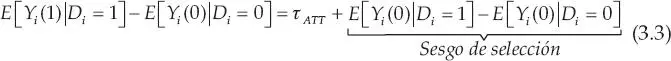

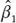 por MCO es un estimador consistente e insesgado del efecto del programa porque E ( ui | Di ) = 0. Es decir, no hay correlación entre la decisión de participar o no en el programa, Di , y las características observadas y no observadas de los individuos contenidas en el término de error, ui . Sin embargo, si la participación en el programa es una decisión de los individuos, 18 es improbable que se cumpla el supuesto E ( ui | Di ) = 0. Esto se presenta porque es posible que los individuos que deciden participar en el programa lo hagan debido a que son sistemáticamente diferentes de los individuos que deciden no participar. Algunas de estas diferencias pueden, a su vez, explicar la variable de resultado, Yi , y, por tanto, estar contenidas en el término de error, ui . Dicho de otra manera, saber si un individuo participa o no participa en el programa informa sobre las variables no observadas del individuo contenidas en ui , por lo cual se invalida el supuesto de independencia condicional.
por MCO es un estimador consistente e insesgado del efecto del programa porque E ( ui | Di ) = 0. Es decir, no hay correlación entre la decisión de participar o no en el programa, Di , y las características observadas y no observadas de los individuos contenidas en el término de error, ui . Sin embargo, si la participación en el programa es una decisión de los individuos, 18 es improbable que se cumpla el supuesto E ( ui | Di ) = 0. Esto se presenta porque es posible que los individuos que deciden participar en el programa lo hagan debido a que son sistemáticamente diferentes de los individuos que deciden no participar. Algunas de estas diferencias pueden, a su vez, explicar la variable de resultado, Yi , y, por tanto, estar contenidas en el término de error, ui . Dicho de otra manera, saber si un individuo participa o no participa en el programa informa sobre las variables no observadas del individuo contenidas en ui , por lo cual se invalida el supuesto de independencia condicional.