

| Tasa de Interés anual (TNA) para compras |
10,99 % (0,03011 %) Tasa de Interés Diaria (TID) |
| Otras tasas anuales |
TNA para adelantos en efectivo: 14,99 % (0,04107 % TID)Tasa Penal: 27,99 % (0,07669 TID) |
Si usted mantiene un saldo de $100 a lo largo del año, usted adeudará 100 * (1,007668)365 a fin de año[12]. Como la hoja demuestra, ello se traduce en 32,286 % TEA (celda B5).

Como usted puede ver en la celda B6, esencialmente el mismo interés puede ser calculado usando capitalización continua. Desde un punto de vista de cálculo, capitalizar en forma continua es más simple que capitalizar en forma discreta una tasa diaria de interés.
Capitalización continua en este libro
Raramente utilizamos capitalización continua en este libro. Utilizamos capitalización discreta, pero ocasionalmente puntualizamos mediante nota al pie, cómo sería el cálculo con capitalización continua de una expresión discreta.
9.3.Retornos con capitalización continua
En subsecciones pasadas hemos medido capitalización discreta versus continua. En esta sección, mostramos cómo medir tasas de retorno discretas versus continuas. Suponga que una inversión crezca desde X en el momento 0 a Y en el momento T. Entonces, la tasa de retorno anual capitalizada en forma discreta sobre la inversión es:

La tasa de retorno anual con capitalización continua está dada por:
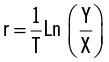
En el ejemplo de abajo, una inversión de $100 crece a $200 en un período de 4 años[13]. La hoja calcula tanto los retornos con capitalización discreta como continua.

La tasa de retorno con capitalización discreta (celda B6) es 18,92 %; esto se prueba en la celda B10, en que mostramos que 200=100*(1+18,92%)4. En otras palabras, a lo largo de los 4 años el valor futuro de $100 con capitalización discreta al 18,92 % es $200.
La tasa de retorno con capitalización continua (celda B7) es 17,33 %; esto se prueba en la celda B11, en que mostramos que 200=100*exp(17,22%*4). A lo largo de los 4 años el valor futuro de $100 con capitalización discreta al 17,32 % es $200.
Observe que para usted será indiferente elegir un retorno anual de 18,92 % con capitalización discreta que un 17,32 % con capitalización continua. Sobre un plazo de tiempo determinado, ¡ambas tasas hacen que una inversión inicial crezca hasta el mismo resultado final!
En este capítulo hemos aplicado el valor del dinero en el tiempo (VA, VAN, y TIR) a un número de problemas relevantes:
 Encontrar la tasa de interés efectiva anual (TEA): esta es la tasa de interés compuesta anual implícita en un activo financiero específico; desde otra perspectiva se puede decir que es la TIR anualizada. Hemos aportado un número de ejemplos —leasing, préstamos hipotecarios, tarjetas de crédito— todos los cuales ilustran que la única manera de evaluar el costo de financiamiento es calculando la TEA.
Encontrar la tasa de interés efectiva anual (TEA): esta es la tasa de interés compuesta anual implícita en un activo financiero específico; desde otra perspectiva se puede decir que es la TIR anualizada. Hemos aportado un número de ejemplos —leasing, préstamos hipotecarios, tarjetas de crédito— todos los cuales ilustran que la única manera de evaluar el costo de financiamiento es calculando la TEA.
 El efecto de períodos de capitalización no anuales: muchas tasas de interés son calculadas sobre una base mensual e incluso diaria. La TEA requiere que anualicemos esas tasas de interés de modo que podamos compararlas. Cuando el número de períodos de capitalización se vuelve muy elevado (como nuestro ejemplo de la Universidad el Estado de Columbia), la TEA = er, donde e= 2,7182818285904 (calculada con =Exp( ) y r es la tasa de interés publicada.
El efecto de períodos de capitalización no anuales: muchas tasas de interés son calculadas sobre una base mensual e incluso diaria. La TEA requiere que anualicemos esas tasas de interés de modo que podamos compararlas. Cuando el número de períodos de capitalización se vuelve muy elevado (como nuestro ejemplo de la Universidad el Estado de Columbia), la TEA = er, donde e= 2,7182818285904 (calculada con =Exp( ) y r es la tasa de interés publicada.
1Estos cargos son comunes en muchos tipos de préstamos bancarios, especialmente hipotecarios. Son obviamente una manera de incrementar el costo del préstamo y confundir al cliente.
2En el mundo real, los pagos son probablemente mensuales; vea el ejemplo en la Sección 3.3.
3Observe que PAGOINT y PAGOPRIN funcionan solo cuando la cuota del préstamo es constante.
4La mayoría de los préstamos hipotecarios son, por supuesto, por un plazo mucho mayor. Pero 12 meses nos permiten ajustar el ejemplo cómodamente en una hoja. Más adelante consideraremos plazos más largos, pero el principio será el mismo.
5Observe que estamos escribiendo los flujos de fondos negativos (como el costo de adquisición del ordenador) como números positivos, por lo que debemos escribir los flujos de fondos positivos como números negativos.
6Una advertencia: estamos tratando al valor residual del ordenador como si tuviera la misma certidumbre que el resto de los flujos de fondos, cuando claramente es menos cierto. La literatura financiera tiene una solución técnica para esto: buscamos el equivalente cierto del valor residual. Por ejemplo, puede ser que esperemos que el valor residual sea de $1.200, pero que —reconociendo la incertidumbre de obtener dicho valor— tratemos ese importe como equivalente a obtener $800 de valor residual con certeza.
7El “precio al público sugerido del fabricante” (PPSF) es el precio que el fabricante sugiere como apropiado para el coche. En realidad, es una especie de precio ficticio oficial y constituye la base para la negociación entre el agente y el adquirente. En nuestro ejemplo, el PPSF es utilizado en el cálculo el valor residual, pero el precio real pagado por el coche es menor.
8Según www.edmunds.com: “los pagos finales del leasing son generalmente razonables, a menos que el coche tenga 100.000 millas y chocolate derretido en la tapicería. Las agencias e instituciones financieras quieren que usted les compre otro coche nuevamente y pueden ser indulgentes en relación al exceso de millas o desgaste anormal. Después de todo, si lo atosigan con un grupo de gastos falsos usted no se mantendrá como un cliente leal, ¿o sí? Pero tenga en mente que si usted lleva su negocio a otra parte, estará recibiendo facturas por neumáticos usados, restos de pintura, golpes en las puertas, etc.”.
9Algunas compañías de leasing actualmente le dan la opción de comprar el coche por el valor residual al finalizar el contrato. Ello efectivamente fija la TEA del leasing, dado que si el automóvil vale más que el valor residual, usted siempre puede comprarlo al valor residual y revenderlo en el mercado.
10El valor residual exacto que a usted le resultará indiferente es $14.134.
11¿Qué es una tasa de interés penal? Como el sitio web explica: “si usted paga tarde, todas las tasas pueden cambiar hacia la misma que la tasa de interés penal”. En otras palabras, si usted demora en el pago, la tasa penal se aplica sobre todos los saldos pendientes.
Читать дальше





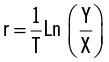

 Encontrar la tasa de interés efectiva anual (TEA): esta es la tasa de interés compuesta anual implícita en un activo financiero específico; desde otra perspectiva se puede decir que es la TIR anualizada. Hemos aportado un número de ejemplos —leasing, préstamos hipotecarios, tarjetas de crédito— todos los cuales ilustran que la única manera de evaluar el costo de financiamiento es calculando la TEA.
Encontrar la tasa de interés efectiva anual (TEA): esta es la tasa de interés compuesta anual implícita en un activo financiero específico; desde otra perspectiva se puede decir que es la TIR anualizada. Hemos aportado un número de ejemplos —leasing, préstamos hipotecarios, tarjetas de crédito— todos los cuales ilustran que la única manera de evaluar el costo de financiamiento es calculando la TEA.










