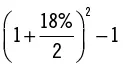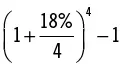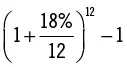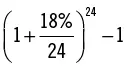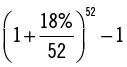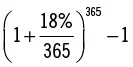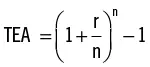Simon Benninga - Principios de finanzas con excel.

TEA = (1 + tasa de interés mensual)12-1

TEA = (1,015)12-1 = 19,56 %

Por ley del Congreso (“The Federal Truth in Lending Act” – “Ley de Prestamos”) quienes efectúan préstamos están obligados a especificar la tasa nominal anual (TNA) cargada en los préstamos. Desafortunadamente, la Ley de Préstamos no indica cómo debe computarse la TNA y el uso el término por parte de quienes otorgan préstamos no es uniforme. A pesar de que “TNA” es la denominación legal designada para ayudar al usuario a entender el verdadero costo del endeudamiento, algunas veces la TNA es la tasa de interés efectiva anual (TEA), pero en otros casos —como en el ejemplo de la tarjeta de crédito de esta sección— la TNA es algo diferente. El resultado es muy confuso.

En el ejemplo precedente, la compañía de tarjeta de crédito toma su interés “anual” de 18 % y lo transforma en 1,5 % de interés mensual. Como vimos, la TEA resultante es 19,56 %.

En la figura 3.2. calculamos el efecto del número de períodos de capitalización sobre la TEA.

La TEA crece con el número de períodos de capitalización. La TEA es:

Cuando lo hacemos en Excel, vemos que la TEA crece a medida que el número de períodos de capitalización se incrementa. Para una cantidad muy grande de períodos de capitalización, la TEA se aproxima al límite de 19,722 % (celda C20 abajo en la siguiente hoja).

Hay dos cuestiones importantes que deben subrayarse sobre el cómputo de la TEA:

Mientras el número de períodos de capitalización por año (n) crece, la TEA se incrementa en:

La tasa a la cual la TEA crece se torna menor a medida que el número de períodos de capitalización aumenta. Hay muy poca diferencia entre la TEA cuando el interés se capitaliza 36 veces por año (TEA = 19,668 %) y la TEA cuando capitalizamos 365 veces por año (TEA = 19,716 %).

LA TASA DE INTERÉS EFECTIVA ANUAL (TEA) Y EL NÚMERO DE PERÍODOS DE CAPITALIZACIÓNLa tasa de interés anual es 18 %
Número de períodos de capitalización por año	Fórmula de TEA	TEA (%)
1	(1+18 %) – 1	18
2 (capitalización semestral)		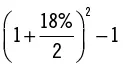18,81
4 (capitalización trimestral)		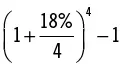19,252
12 (capitalización mensual)		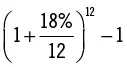19,562
24 (capitalización quincenal)		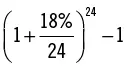19,641
52 (capitalización semanal)		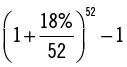19,685
365 (capitalización diaria)		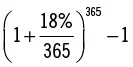19,716
Figura 3.2. La TEA cuando la tasa de interés anual de 18 % se capitaliza varias veces por año.

En la celda C20 hemos computado el límite de la TEA cuando el número de períodos de capitalización se torna muy elevado. Este límite se llama capitalización continua. Para n períodos de capitalización por año:

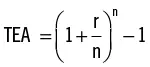
Cuando el número de períodos de capitalización n se torna demasiado alto, la TEA sea aproxima a er-1. El número e = 2,7182818285904 es la base de logaritmos naturales y está incluida en la función Exp( ) de Excel. En la jerga de finanzas, erT se denomina valor futuro con capitalización continua después de T años a la tasa de interés anual r.

En la hoja de abajo usted podrá ver la diferencia entre el valor futuro con capitalización discreta y valor futuro con capitalización continua.

Cuando el número de períodos de capitalización se vuelve muy elevado, la diferencia entre el interés con capitalización discreta y continua se torna muy reducido.

En el capítulo 2 vimos que el valor futuro y valor presente están estrechamente relacionados:

La siguiente hoja sintetiza estas relaciones:

El interés con capitalización continua puede parecer un concepto etéreo —altamente teórico— pero es muy útil. El ejemplo de esta subsección muestra cuán ventajoso puede ser el interés con capitalización continua. La tarjeta de crédito de la Universidad del Estado de Columbia de la imagen siguiente carga un interés penal anual (TNA) del 27,99 %[11]. El paréntesis del aviso deja en claro que la empresa realmente carga un 0,07669 % por día sobre los saldos pendientes. Esta tasa se calcula tomando el 27,99 % y dividiéndolo por el número de días por año: