Simon Benninga - Principios de finanzas con excel.

Usted puede “jugar” con la hoja de cálculo, ajustando la celda B2 hasta que la celda C9 sea igual a cero. Por ejemplo, si pone $5.000 en la celda B2 observará que el VAN en la celda C9 es negativo, indicando que Mario está ahorrando demasiado poco.

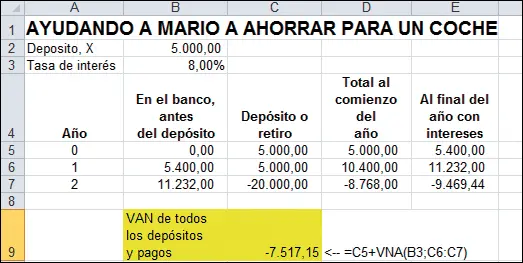
Si pone 10.000$ en la celda B2, la celda C9 será positiva: ello indica que la respuesta está en algún lugar entre 5.000 y 10.000. Mediante prueba y error usted puede llegar a la respuesta correcta.

Buscar objetivo es una función de Excel que busca un número específico en una celda ajustando el valor de otra celda (para una revisión sobre el uso de Buscar Objetivo, vea el capítulo 21). Para resolver el problema de Mario, podemos usar Buscar Objetivo para hacer que la celda C9 sea igual a 0. En el menú de Excel 2007 se selecciona Datos l Herramientas de Datos l Análisis Y Si l Buscar Objetivo.

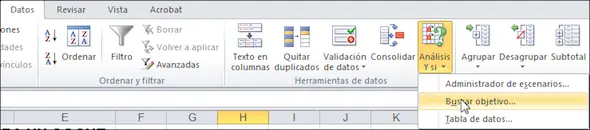
Habiendo elegido Buscar Objetivo veremos el cuadro de diálogo que aparece a continuación:

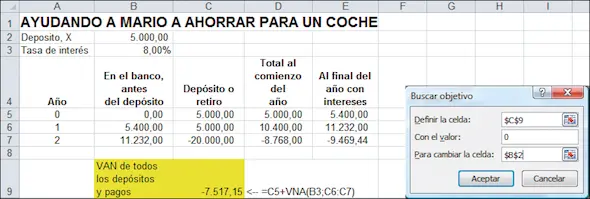
Y al hacer clic en Aceptar, Buscar Objetivo encontrará la solución de $8.903,13.

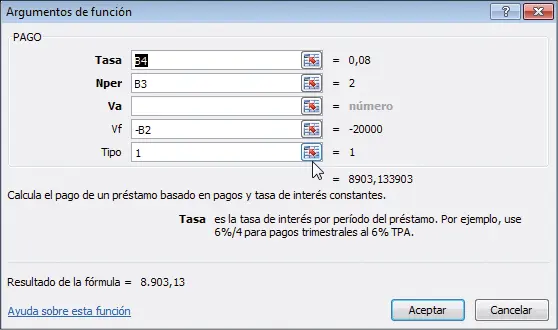
La función PAGO de Excel puede resolver directamente el problema de Mario, como se ilustra en la siguiente hoja:

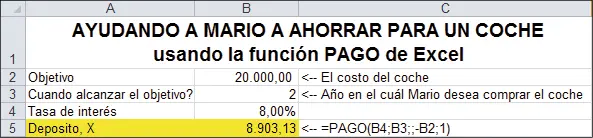
El cuadro de diálogo para esta función se presenta a continuación:

En esta sección presentamos 2 versiones más complicadas que el problema de Mario de la sección 2.8.

Comenzamos intentando determinar si los padres de una niña pequeña están ahorrando suficiente dinero para su educación universitaria. A continuación el problema:

El día en que Nerea García cumplió 10 años sus padres decidieron depositar $4.000 en una cuenta bancaria para su hija. Ellos pretenden depositar $4.000 adicionales en la cuenta cada año el día de su cumpleaños de 11, 12… hasta el de 17.

Todos los saldos bancarios generan un 8 % de interés.

El día del cumpleaños de 18, 19, 20 y 21, sus padres sacarán $20.000 para pagar la universidad.

¿Son los $4.000 anuales suficientes para cubrir los aranceles universitarios previstos? Podemos resolver fácilmente este problema en una hoja.

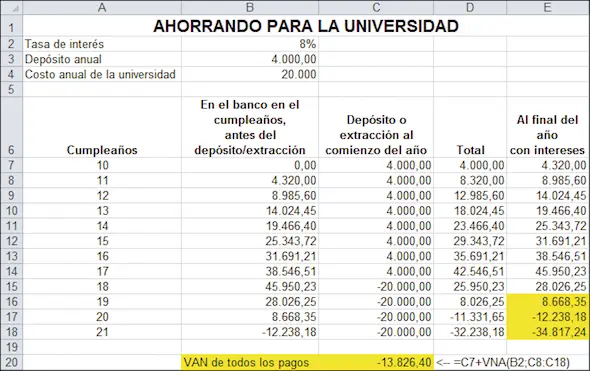
Observando la columna de saldo al final del año en la columna E, los $4.000 no son suficientes —Nerea y sus padres se quedarán sin dinero en algún momento entre el cumpleaños 19 y 20[5]—. Al final de su carrera universitaria habrá $34.817 “en descubierto” (celda E18). Otra forma de verlo es observar el cálculo de VAN en la celda C20: como vimos en la sección anterior, un plan que combina depósitos / extracciones está completamente financiado cuando el VAN de todos los pagos / extracciones es cero. En la celda C20 se comprueba que el VAN es negativo – El plan de Nerea es subfinanciado.

¿Cuánto deberán ahorrar los padres de Nerea cada año? Hay muchas maneras de responder a esta pregunta, en las cuales se profundizará más adelante. Estos métodos son básicamente iguales que los tratados para resolver el problema de Mario presentado en la sección anterior, pero para que quede completo vamos a presentarlos nuevamente.

Asumiendo que usted ha puesto las fórmulas correctas en la hoja, puede “jugar” con la celda B3 hasta que la celda E18 o la celda C20 sean igual a cero. Haciéndolo podemos ver que los padres de Nerea deberían haber planeado depositar $6.227,78 anualmente.

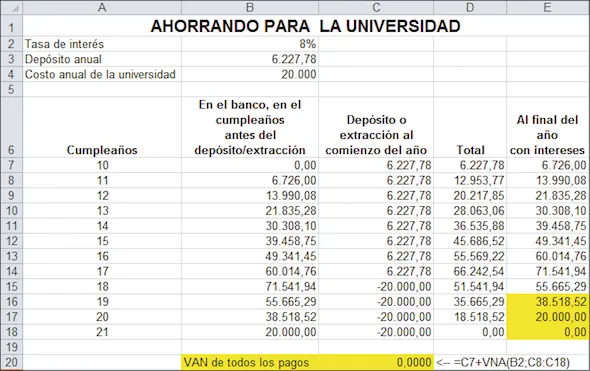
Note que el VAN de todos los pagos (celda C20) es cero cuando la solución es alcanzada. Los pagos futuros son totalmente financiados cuando el VAN de todos los flujos de fondos es cero.

Podemos usar Buscar Objetivo para hacer que la celda E18 sea cero. Tras pulsar en Datos l Herramientas de Datos l Análisis Y Si l Buscar Objetivo, se completa el cuadro de diálogo.

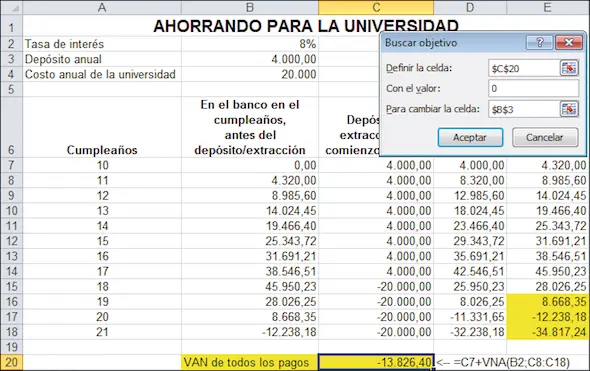
Cuando se hace clic en Aceptar, Buscar Objetivo busca la solución. El resultado es el mismo que antes: $6.227,78.

Podemos usar VA de Excel y la función PAGO para resolver este problema directamente, como se ilustra en la siguiente hoja.

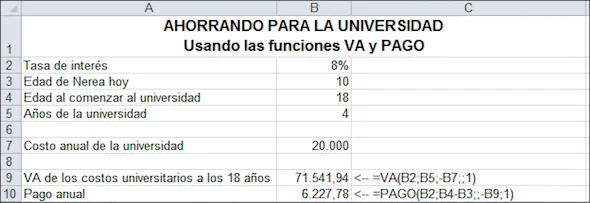
Explicación: la celda B9 es el valor actual de los aranceles universitarios al comenzar los 18 años de edad. La función PAGO computa el pago anual requerido tal que el valor futuro de los pagos (capitalizados al 8 % durante 8 años) sea igual a $71.541,94.

Podemos, por supuesto, integrar la función VA en la función PAGO, de modo que la solución sea aún más simple.

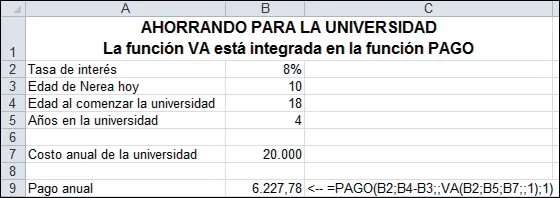
El problema de ahorro de los padres de Nerea es exactamente el mismo que el que enfrenta un individuo que pretende ahorrar para su retiro. Suponga que Joe tiene 20 años hoy y desea comenzar a ahorrar de modo que cuando tenga 65 pueda disponer durante 20 años de $100.000 para retirar anualmente. Adaptando la hoja previa, obtenemos lo siguiente.

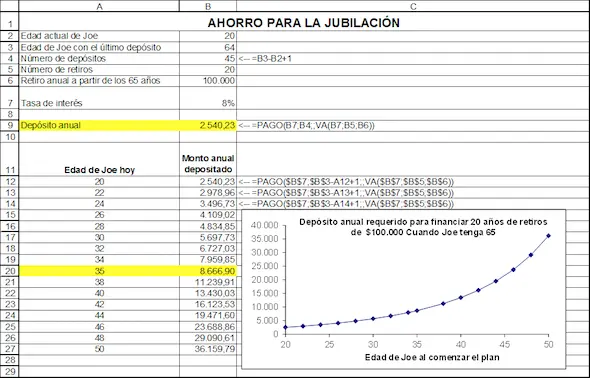
En la tabla, en las filas 12-27 usted ve el poder del interés compuesto: si Joe comienza a ahorrar a la edad de 20 años para su retiro, un depósito de $2.540,23 crecerá para proveerle de sus $100.000 necesarios de jubilación durante 20 años a partir de la edad de 65 años. Por otro lado, si comienza a ahorrar a la edad de 35 años, necesitará $8.666,90 anuales.