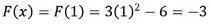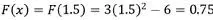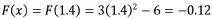Por su parte, cuando se compara el valor asignado a la variable con su valor real o esperado, se le conoce como error absoluto; si este se expresa de manera porcentual (ecuación 1.6) se le llama comúnmente porcentaje de error (%error).

Por fuera de un contexto fenomenológico o sin una definición del máximo error relativo, error absoluto o tolerancia permitida para resolver la ecuación 1.1, cualquier cantidad de cifras usada para 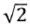 (por ejemplo 1.41, 1.414, 1.4142, etc.) es correcta, pues todos coinciden con el valor de referencia o valor real para esa cantidad y, por lo tanto, se puede afirmar que cualquiera de esos valores describe con exactitud el valor de
(por ejemplo 1.41, 1.414, 1.4142, etc.) es correcta, pues todos coinciden con el valor de referencia o valor real para esa cantidad y, por lo tanto, se puede afirmar que cualquiera de esos valores describe con exactitud el valor de 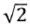 . La diferencia radica en que a medida en que se aumentan las cifras decimales, la cantidad se describe con mayor precisión, pues una eventual variación alrededor del valor asignado tendrá menor incidencia en los resultados (por ejemplo, al evaluarlo en la ecuación 1.1).
. La diferencia radica en que a medida en que se aumentan las cifras decimales, la cantidad se describe con mayor precisión, pues una eventual variación alrededor del valor asignado tendrá menor incidencia en los resultados (por ejemplo, al evaluarlo en la ecuación 1.1).
En otras palabras, 1.41 es un valor exacto para describir 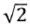 , pero menos preciso que 1.4142, o 1.4142 es más preciso que 1.414 para describir
, pero menos preciso que 1.4142, o 1.4142 es más preciso que 1.414 para describir 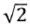 , aunque ambos valores son exactos.
, aunque ambos valores son exactos.
1.2 Algoritmos e iteraciones
Para continuar ilustrando otros conceptos, se usará otra estrategia de solución (diferente a la analítica) para resolver el problema de encontrar el valor de x que satisface la ecuación 1.1.
Partiendo del supuesto de que aún no se conocen métodos numéricos para resolverlo, se utilizará tanteo y error para encontrar la solución, es decir, se asignarán diferentes valores a x y se evaluará cada uno en la ecuación 1.1 hasta obtenerse un valor de x que satisfaga la condición F(x) = 0 (dentro de una tolerancia definida).
Si la asignación de valores a la variable x se hace de manera aleatoria, es decir, asignando valores sin seguir patrones o tendencias, la probabilidad de acertar el resultado es muy limitada, pues será cuestión de suerte encontrar la solución. Además, la probabilidad de encontrar la solución estará condicionada por la tolerancia definida: para grandes tolerancias (o mayor error permitido), seguramente se llegará a la respuesta con menor cantidad de cálculos (menor tiempo y esfuerzo) pero esta será poco precisa. Para tolerancias más pequeñas (o menor error permitido), probablemente se requiera mayor cantidad de cálculos (mayor tiempo y esfuerzo) pero se tendrá mayor precisión.
Para aumentar la probabilidad de llegar al resultado sin depender de la suerte para lograrlo (independiente de la tolerancia o error permitido que se defina), puede utilizarse un algoritmo de solución, es decir, una serie o secuencia lógica de pasos que den un “orden” a los cálculos mientras se busca la solución del problema.
Por ejemplo, en lugar de asignar valores aleatorios a la variable por tanteo y error, puede intentarse implementar los pasos que se describen en la tabla 1.1, donde se puede observar que, para llegar a la solución, inicialmente se ejecutaron los pasos 1 al 4 del algoritmo y luego se repitió del paso 2 al 4 en tres ocasiones. Cada una de esas repeticiones en los pasos del algoritmo se llama iteración o etapa de cálculo.
Tabla 1.1 Ejemplo de un algoritmo para agilizar el tanteo y error en busca de una solución para la ecuación 1.1
| Paso |
Acción |
Ejemplo de ejecución |
| 1 |
Asigne arbitrariamente un valor inicial a la variable x |
Para efectos ilustrativos suponga x = 2 |
| 2 |
Evalúe la función (ecuación 1.1) en el valor asignado a la variable |
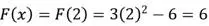 |
| 3 |
Compare el resultado del paso 2 con el valor esperado para la función (dentro de una tolerancia permitida τ) |
Para efectos ilustrativos suponga τ = 2 x 10–1 = 0.20 ± τ = [0 – 0.2, 0 + 0.2] |
| 4 |
Si el resultado en el paso 3 es F(x) > (0 + τ), asigne un nuevo valor a x que sea menor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) < (0 – τ), asigne un nuevo valor a x que sea mayor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) 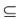 [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado |
6 > (0 + 0.2); por lo tanto, el nuevo x debe ser un valor < 2. Para efectos ilustrativos suponga x = 1 |
| Repita 2 |
Evalúe la función en el valor asignado a la variable |
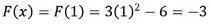 |
| Repita 3 |
Compare el resultado con el valor esperado para la función (dentro de la tolerancia permitida) |
0 ± τ = [0 – 0.2, 0 + 0.2] |
| Repita 4 |
Si F(x) > (0 + τ), asigne un nuevo valor a x que sea menor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) < (0 – τ), asigne un nuevo valor a x que sea mayor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) 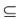 [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado |
–3 < (0 – 0.2); por lo tanto, el nuevo x debe ser un valor > 1. Para efectos ilustrativos suponga x = 1.5 |
| Repita 2 |
Evalúe la función en el valor asignado a la variable |
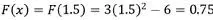 |
| Repita 3 |
Compare el resultado del valor esperado para la función (dentro de la tolerancia permitida) |
0 ± τ = [0 – 0.2, 0 + 0.2] |
| Repita 4 |
Si F(x) > (0 + τ), asigne un nuevo valor a x que sea menor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) < (0 – τ), asigne un nuevo valor a x que sea mayor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) 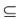 [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado |
0.75 > (0 + 0.2); por lo tanto, el nuevo x debe ser un valor < 1.5. Para efectos ilustrativos suponga x = 1.4 |
| Repita 2 |
Evalúe la función en el valor asignado a la variable |
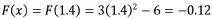 |
| Repita 3 |
Compare el resultado con el valor esperado para la función (dentro de la tolerancia permitida) |
0 ± τ = [0 – 0.2, 0 + 0.2] |
| Repita 4 |
Si F(x) > (0 + τ), asigne un nuevo valor a x que sea menor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) < (0 – τ), asigne un nuevo valor a x que sea mayor que el utilizado en la etapa anterior y repita a partir del paso 2.Si el resultado es F(x) 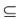 [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado |
–0.12 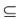 [0 – 0.2, 0 + 0.2]; por lo tanto, el resultado x = 1.4 es válido dentro de la tolerancia definida y será una solución al ejercicio [0 – 0.2, 0 + 0.2]; por lo tanto, el resultado x = 1.4 es válido dentro de la tolerancia definida y será una solución al ejercicio |
Para facilitar el análisis del comportamiento o progreso del algoritmo de la tabla 1.1, en la tabla 1.2 se registran los resultados de la función al evaluarla en cada iteración.
Читать дальше


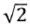 (por ejemplo 1.41, 1.414, 1.4142, etc.) es correcta, pues todos coinciden con el valor de referencia o valor real para esa cantidad y, por lo tanto, se puede afirmar que cualquiera de esos valores describe con exactitud el valor de
(por ejemplo 1.41, 1.414, 1.4142, etc.) es correcta, pues todos coinciden con el valor de referencia o valor real para esa cantidad y, por lo tanto, se puede afirmar que cualquiera de esos valores describe con exactitud el valor de 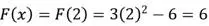
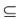 [0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado
[0 – τ, 0 + τ], finalice el ejercicio y reporte el resultado