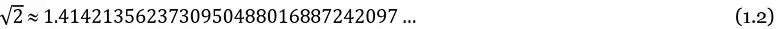1.1 Errores y tolerancia
Suponga que necesita determinar el valor de x que satisface la ecuación 1.1:

La solución analítica o exacta al problema se logra aplicando métodos, fórmulas o procedimientos matemáticos convencionales, en este caso despejando la variable paso a paso de la siguiente manera:
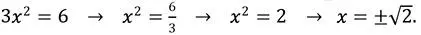
De este modo, se obtiene que el valor de x = 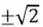 corresponde a la respuesta exacta (para simplificar en adelante se tomará solo su parte positiva), pues al sustituir la x por el valor de
corresponde a la respuesta exacta (para simplificar en adelante se tomará solo su parte positiva), pues al sustituir la x por el valor de 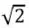 en la ecuación 1.1, el lado izquierdo de la expresión es exactamente igual a 0 y se cumple la igualdad.
en la ecuación 1.1, el lado izquierdo de la expresión es exactamente igual a 0 y se cumple la igualdad.
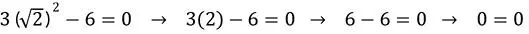
Ahora suponga que es necesario expresar 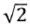 como un número fraccionario antes de sustituirlo en la ecuación 1.1. Por si no lo recordaba,
como un número fraccionario antes de sustituirlo en la ecuación 1.1. Por si no lo recordaba, 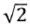 es un número irracional (ecuación 1.2), así que para llevarlo a la ecuación 1.1 necesariamente debe redondearse a un número finito de cifras decimales.
es un número irracional (ecuación 1.2), así que para llevarlo a la ecuación 1.1 necesariamente debe redondearse a un número finito de cifras decimales.
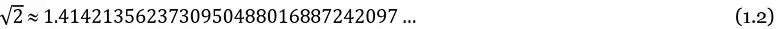
La diferencia entre la cifra real (con infinitas cifras decimales) y la que se utilice para representar 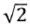 (por ejemplo 1.41, 1.414, 1.4142, 1.41421, etc.) se conoce como error de redondeo. De hecho, incluso al utilizar la expresión
(por ejemplo 1.41, 1.414, 1.4142, 1.41421, etc.) se conoce como error de redondeo. De hecho, incluso al utilizar la expresión 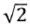 en una calculadora o un equipo de cómputo, este se limita o redondea a la cantidad de cifras que pueda almacenar según la capacidad de cómputo del equipo o programa utilizado o, en otras palabras, de manera voluntaria (si usted decide o asume cuántas cifras utilizar) o involuntaria (si utiliza toda la capacidad —aunque finita— de su calculadora o equipo de cómputo) se introduce un error de redondeo en los cálculos.
en una calculadora o un equipo de cómputo, este se limita o redondea a la cantidad de cifras que pueda almacenar según la capacidad de cómputo del equipo o programa utilizado o, en otras palabras, de manera voluntaria (si usted decide o asume cuántas cifras utilizar) o involuntaria (si utiliza toda la capacidad —aunque finita— de su calculadora o equipo de cómputo) se introduce un error de redondeo en los cálculos.
En algunas ocasiones se podría tener un error significativo (que afecte o desvíe los resultados más allá de un límite permitido). La medida común para expresar ese “límite permitido”, dentro del cual se pueden aceptar desviaciones en los resultados, se conoce como tolerancia, la cual se debe definir, a menos que el contexto del problema en particular permita inferirla.
Para explicar ese concepto, observe lo que ocurre al sustituir x = 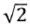 en la ecuación 1.1 usando dos (ecuación 1.3), tres (ecuación 1.4) o cuatro (ecuación 1.5) cifras decimales en el valor de la variable. Para efectos de comparación se expresa el resultado con 4 cifras decimales en todos los casos.
en la ecuación 1.1 usando dos (ecuación 1.3), tres (ecuación 1.4) o cuatro (ecuación 1.5) cifras decimales en el valor de la variable. Para efectos de comparación se expresa el resultado con 4 cifras decimales en todos los casos.

Puede notarse que para ninguna de las tres situaciones (ecuaciones 1.3, 1.4 y 1.5) la respuesta es = 0, que es lo esperado según la ecuación 1.1. Sin embargo, a medida que se aumenta el número de cifras decimales para expresar 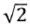 , el resultado de la operación se hace más cercano a 0 (al menos dentro de las cifras decimales utilizadas en las respuestas).
, el resultado de la operación se hace más cercano a 0 (al menos dentro de las cifras decimales utilizadas en las respuestas).
Por ejemplo, de acuerdo con la ecuación 1.3, afirmar que 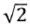 = 1.41 (lo cual es cierto al redondear) implica aceptar que el valor –0.0357 = 0 (según las ecuaciones 1.1 y 1.3), lo cual, en un lenguaje estrictamente matemático, es incorrecto. Ahora, en un contexto hipotético donde se afirme que la temperatura ambiente de un lugar a una hora específica es 25 °C todo el año, pero un día en particular disminuyó 0.0357 °C, registrando 24.9643 °C, y considerando además aspectos como que la temperatura se mide con termómetros de mercurio que disponen para ello de una escala de 0 a 100 °C, es perfectamente válido afirmar que la temperatura todo el año fue de 25 °C e ignorar la pequeña variación que se registró, es decir, asumir que la variación de 0.0357 es equivalente a ninguna variación, o, en otras palabras, aceptar que en ese contexto –0.0357 ≈ 0.
= 1.41 (lo cual es cierto al redondear) implica aceptar que el valor –0.0357 = 0 (según las ecuaciones 1.1 y 1.3), lo cual, en un lenguaje estrictamente matemático, es incorrecto. Ahora, en un contexto hipotético donde se afirme que la temperatura ambiente de un lugar a una hora específica es 25 °C todo el año, pero un día en particular disminuyó 0.0357 °C, registrando 24.9643 °C, y considerando además aspectos como que la temperatura se mide con termómetros de mercurio que disponen para ello de una escala de 0 a 100 °C, es perfectamente válido afirmar que la temperatura todo el año fue de 25 °C e ignorar la pequeña variación que se registró, es decir, asumir que la variación de 0.0357 es equivalente a ninguna variación, o, en otras palabras, aceptar que en ese contexto –0.0357 ≈ 0.
Lo anterior sirve para aseverar que en muchas ocasiones la decisión sobre qué tantas cifras decimales o cifras significativas utilizar para expresar una cantidad gira en torno a la naturaleza de los datos del fenómeno o situación que se desea representar. Por ejemplo, si un dato representa una temperatura medida en grados Celsius (°C), es normal utilizar solo dos cifras decimales, ya que la mayoría de los equipos de medición y control para esa variable (al menos los termómetros y termocuplas comunes) limitan hasta allí la posibilidad de lecturas confiables. En otro contexto, si el dato representa una concentración medida en mol por litro (mol/L), es bastante común utilizar 4 cifras decimales.
Dado que para el ejemplo de la ecuación 1.1 no se provee información alguna sobre la naturaleza del problema en cuestión, es necesario definir algún criterio o condición que se deba cumplir para verificar que la respuesta es correcta dentro del contexto del problema.
En el caso de las ecuaciones 1.3, 1.4 y 1.5, si para el problema se define una tolerancia de 1 x 10–4, implicaría que solo el valor x = 1.4142 es correcto, pues es el único para el que, al evaluar la función, la diferencia (en valor absoluto) entre el resultado obtenido (–0.0001) y el resultado esperado (0) es menor o igual a 1 x 10–4. Por otro lado, para una tolerancia de 1 x 10–1, cualquiera de los valores x = 1.41, x = 1.414 o x = 1.4142 sería correcto, ya que los tres resultados correspondientes al evaluar la función (–0.0357, –0.0018 y –0.0001) satisfacen el criterio dado por esa tolerancia.
En otras palabras, dependiendo de la cantidad de cifras decimales a las que se redondee el resultado de las ecuaciones 1.3, 1.4 y 1.5, se puede asumir que son = 0 o se puede afirmar que son ≠ 0.
Otro criterio utilizado comúnmente para corroborar si al asignar diferentes valores a una variable (en el caso del ejemplo, usando diferente cantidad de cifras decimales) se modifica significativamente el resultado es el error relativo. Este consiste en determinar la diferencia (como valor absoluto o en forma porcentual) entre dos valores diferentes asignados a la variable y comparar si tal diferencia se encuentra dentro de unos límites previamente definidos para tal variabilidad.
Читать дальше


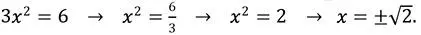
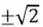 corresponde a la respuesta exacta (para simplificar en adelante se tomará solo su parte positiva), pues al sustituir la x por el valor de
corresponde a la respuesta exacta (para simplificar en adelante se tomará solo su parte positiva), pues al sustituir la x por el valor de 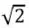 en la ecuación 1.1, el lado izquierdo de la expresión es exactamente igual a 0 y se cumple la igualdad.
en la ecuación 1.1, el lado izquierdo de la expresión es exactamente igual a 0 y se cumple la igualdad.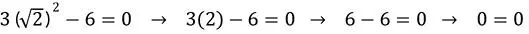
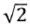 como un número fraccionario antes de sustituirlo en la ecuación 1.1. Por si no lo recordaba,
como un número fraccionario antes de sustituirlo en la ecuación 1.1. Por si no lo recordaba,