Example IIIProgressive Insurance observed that when its policyholders hired a lawyer to settle a claim, settlement time went up from 90 days to 6 months, and the payout to the policyholder went down by $100. The costs to Progressive increased by $1600 due to the need to engage lawyers for these cases. Clearly, policyholders (and Progressive) would be better served if lawyers were not needlessly involved in the process. To achieve this goal, the project team focused on the dependent variable: percentage of claimants who hired an attorney within 60 days of the accident, which had been about 36%. Brainstorming produced 59 ideas for reducing this percentage; excluding ideas that were not “practical, fast, or cost‐free” culled the number to 19. This number finally was reduced to 13, which were tested via designed experiments. When all was said and done, the percentage was reduced by eight points, with each one‐point drop representing six million dollars in savings and better service to policyholders.
One of the more surprising innovations as a result of this experiment was that Progressive began paying out more in claims! If a person's car is totaled in an accident and the insurance company insists on paying book value rather than replacement value, what is the person likely to do? Hire a lawyer! In the experiment, districts that paid more in claims had a five‐point drop in attorney involvement. The decrease in legal fees more than made up for the increase in payments to policyholders.
Example IVA company that sold telecommunications equipment to large corporations contemplated changing its customer management system to a desk‐based account manager (DBAM) system. These account managers would not work from the field, but solely from the office, making use of the telephone and video calls. This would save on travel time, increase efficiency, and, hopefully, lead to greater profit. A small number of field account managers were provided with the DBAM and trained in its use. The accounts of these managers were the experimental group. A carefully matched set of accounts from other managers constituted the control group. (We will discuss matching in Chapter 5.)
Various measures on customer satisfaction and employee satisfaction were taken on each group before and after the experiment. Costs and revenues associated with each group were measured as well. The key performance indicator (KPI) for the experiment was cost‐to‐revenue ratio. The experimental group had a KPI that was 6% lower than the control group; this implies that the DBAM was more profitable than the existing method. The ancillary measures showed that employee satisfaction did not decrease and customer satisfaction actually increased. The primary reason for the increased customer satisfaction was that it was easier for customers to contact their representatives, who were no longer unavailable while traveling. The company rolled out the DBAM to all its field agents and increased its profits while increasing customer satisfaction.
Example VAnheuser‐Busch, a beer company, wanted to determine how much money to spend on advertising. The sample of 15 marketing areas was divided into three groups: (i) 50% increase, (ii) no change, and (iii) 25% decrease in advertising expenditure over a 12‐month period. At the end of the experiment, group i achieved a 7% increase in sales, group ii had no change, and group iii had a 14% increase! A follow‐up experiment produced the same result, something that no one ever expected: decreasing advertising produced an increase in sales. This led the firm to conclude that they had supersaturated the market with advertising, and indeed the firm substantially reduced advertising without hurting sales in other markets.
1.4.1 Four Steps of an Experiment
From the previous examples, we can list the four steps of an experiment:
1 Randomly divide the subjects (e.g. customers) into groups. The researcher does not allow the subjects to pick the group – that would be a form of self‐selection that makes the data observational rather than experimental. Moreover, this division is made randomly – the researcher doesn't assign the groups for that, too, would be a form of selection that would render the data observational.
2 Expose each group to a different treatment. The researcher does not allow the subjects to choose which treatment to receive; this assignment has to made randomly.
3 Measure a response for each group. The outcome of interest has to be chosen before the experiment is conducted, and the method for performing the measurement has to be decided in advance, too.
4 Compare group responses to determine which treatment is better. This is accomplished with a statistical test. It can be something as simple as a two‐sample test of means. Whatever test is applied, the test will tell us whether the difference between the groups could be just random or is more likely due to some systematic effect.
We know that observational data can only give correlations and they can't give causation. When we have a well‐designed experiment, we can answer causal questions: Does changing 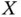 cause a change in
cause a change in 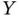 ? Experiments are a systematic way to avoid lurking variables and are the gold standard for causal inference. Thomke Thomke (2020, chapter 2) describes an example of this phenomenon:
? Experiments are a systematic way to avoid lurking variables and are the gold standard for causal inference. Thomke Thomke (2020, chapter 2) describes an example of this phenomenon:
[Yahoo did a study] to assess whether display ads for a brand, shown on Yahoo sites, can increase searches for the brand name or related keywords. The observational part of the study estimated that ads increased the number of searches by 871 percent to 1,198 percent. But when Yahoo ran a controlled experiment, the increase was only 5.4 percent. If not for the control, the company might have concluded that the ads had a huge impact and wouldn't have realized that the increases in searches was due to other variables that changed during the observation period.
1.4.2 Big Three of Causality
The “Big Three” criteria for being able to make causal inference are as follows:
1 When changed, also changed. If changes and doesn't change, then we cannot assert that causes (sometimes this is useful information).
2 happened before . If happens after , then cannot cause . This issue arises sometimes in marketing research, where a commercial is shown one day and sales on that same day are measured. How can we know that today's sales weren't affected by something that happened yesterday?
3 Nothing else besides changed systematically. If variables and change at the same time that changes – not every time, but often enough – then we cannot rule out the possibility that and are causing the changes in . Observational data cannot rule out this possibility. The random treatment assignment of an experiment can rule this out.
Experimentation is the art of making sure these criteria are met so that valid causal statements can be made. Much more will be said about this in the next two chapters. The problem with observational data is that at least one of three is always missing, usually the third.
You should consider performing an experiment when you have lots of items on which to experiment (i.e. “experimental units”), you have the capability to take measurements on these units and the outcomes from the experiments can be measured easily, and you have control over the treatments. In manufacturing, for example, lots of items come off the assembly line, so there is an abundance of experimental units. Measurement typically is easy: Does the item work or how well does it work? Often it is very easy to apply treatments to some units and not to others.
Читать дальше

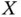 cause a change in
cause a change in 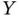 ? Experiments are a systematic way to avoid lurking variables and are the gold standard for causal inference. Thomke Thomke (2020, chapter 2) describes an example of this phenomenon:
? Experiments are a systematic way to avoid lurking variables and are the gold standard for causal inference. Thomke Thomke (2020, chapter 2) describes an example of this phenomenon:










