Jean Sulem - Instabilities Modeling in Geomechanics

Physically, instability may mean many things depending on the type of material and on the geometrical scale of consideration. In the plainest case, a macroscopically homogeneous material element in a laboratory under sufficiently low stress deforms in a homogeneous manner when a uniform traction is applied at its boundary. However, for unspecified physical reasons, at a certain stress level it responds with an unconstrained strain to, for example, a small stress perturbation. Often, the homogeneous strain is associated with a diffuse dilatancy (increased volume). This is a classical representation of instability. The key point is the homogeneity of the response maintained during the unstable phase.

Alternatively, we perceive as critical a loss of uniqueness of response, which means that a repetition of what is theoretically the same experiment would yield a different, still homogeneous, response. An additional option is to treat as unstable a response in which the increase in internal energy over a virtual displacement is less than the work of the external forces. Each of the above critical conditions, in principle, leads to a different criterion, both locally and globally.

In addition, when in a homogeneous sample the straining becomes more advanced, this strain homogeneity may be spontaneously lost. It is inevitable that, due to the actual irregularities in the distribution of minerals with a different stiffness, interface properties, pre-existence of structural defects, etc., high concentrations of stress and/or strain occur. Such concentrations may result in various forms of local damage, like mineral decohesion, micro-fissures, nucleation of pores, and intermineral or intergrain slips, depending on the structure, mineralogy and history of the material. The interaction of such local singularities gives rise to a variety of failure mechanisms. Despite their differences, their common feature is the possibility of microdefects developing into large-scale mechanisms of failure, such as slip-surface, fault or compaction band, leading to landslides, sinkholes, faulting, subsidence, etc. Such mechanisms are often characterized as macroscopic strain localization, when certain features of continuity abruptly cease to persist, like intergranular or intermineral phase contact. Commonly, more than one mechanism occur simultaneously, as in Figure 1.1, which was obtained for a sample of sand, and in which two separate slip surfaces and a substantial volume of diffuse dilatancy are observed after a triaxial compression test.

A mathematical representation of the physics above is equally complex. Often, Lyapunov-type instability (defined as an unconstrained response to a limited perturbation) is implied to result from the solution of a system of differential equations describing the nonlinear material behavior. The instability consists of bifurcation of the solution of the system of equations, which clearly implies that the solution is not unique.

Figure 1.1. Multiple shear bands and a volume increase due to diffuse dilatancy

The criteria for exclusion of instability may be local (or for uniformly deformed systems) or global for a piece of continuum. There are several different criteria, expressing very similar, but not identical conditions.

The first type of criteria refers to certain characteristics of material energy or work required to deform in a unique manner (meaning one uniform solution) under the conditions of equilibrium, for a specific stress–strain relationship and geometrical strain–displacement relationship. The second type allows for strain localization, with a particular geometrical form of deformed configuration that satisfies the conditions of equilibrium that allow certain forms of discontinuity, that is, it admits a certain type of discontinuity (shear or compaction bands). Global criteria consist of the same requirements but integrated over the entire volume of the considered body. The very definition of “bifurcation point” varies from author to author, although in any specific situation there is usually no doubt about what should be called a bifurcation point. The above types of instabilities and their implications have been studied in the context of geomaterials for nearly 50 years, and an example of their implications and their relationships is reproduced in Figure 1.2from an old paper (Bigoni and Hueckel 1991a). The most interesting (to this writer) recent developments concern geomaterials in their multiphysics context.

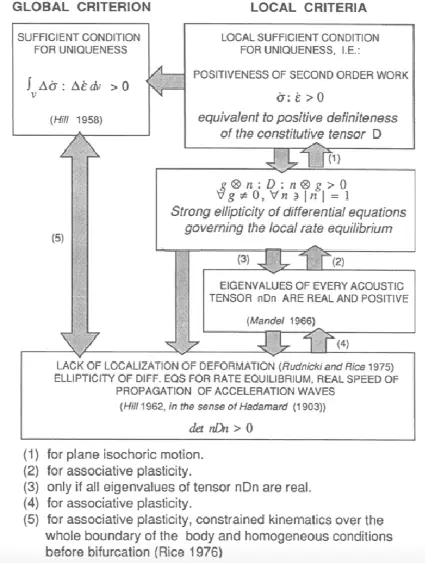
Figure 1.2. Relationships between criteria for uniqueness, second-order work, strong ellipticity, Mandel’s stability and localization

To start with we will limit ourselves to considering exclusively incipient elastoplastic straining at small strains. At the moment, we will not deal with materials that exhibit strong viscous effects.

In what follows, we will outline the basic formulae of elasto-plasticity (equation [1.1]) at small strains to introduce basic concepts that will be referred to (Roscoe and Burland 1968). The given set of equations implies the existence of a yield limit, f = f ( p ′, q , r , pc ′) in the effective stress invariant space, which means yielding if f = 0, and means an elastic unloading state if f < 0. The case of f > 0 is deemed as statically inadmissible. The core of the multiphysical aspects of soil/sediment/rock behavior is embedded in the last of the equations, which describes the evolution of the principal mechanical property of the material, which is the size of the yield locus pc ′ = pc ′ ( εpl , μ (Δ T , ξ , c ... ))with changes in a series of the environmental (non-mechanical) variables (see, for example Hueckel 1992, 2002).

[1.1]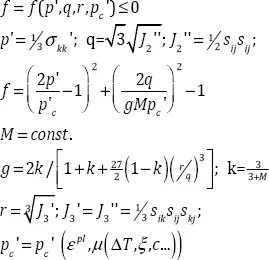

That implies that variables such as temperature, chemical mass removal (accretion) and ion concentration of pore fluid essentially affect the geomaterial strength, apparent preconsolidation pressure and elasto-plastic stiffness.

As is customary in inelasticity theories, the deformation can only be uniquely determined for an incremental stress, rather than total stress, as in elasticity. Therefore, the plastic strain rate is defined as

[1.2]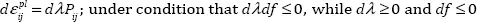

where Pij is the gradient of the plastic potential, or a resultant direction tensor of all inelastic strain components of various origins, including the irreversible change in elasticity due to plastic straining or damage (Hueckel 1975, 1976; Maier and Hueckel 1979; Bigoni and Hueckel 1991a, 1991b; Bigoni 2012). Most of the physical evidence suggests that Pij ≠ Qij, where 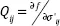is the yield locus gradient, but for a number of reasons it is often seen as convenient to ignore the difference.

Non-associativity, i.e. when Pij ≠ Qij (for instance via an elasto-plastic coupling), or any other forms of irreversible (not necessarily mechanical) straining leading to a non-symmetrical stress–strain incremental relationship, are notorious for inducing a premature loss of stability and/or strain localization.