Skewness for a positively skewed distribution is greater than 0; these distributions have tails that stretch out into values on the abscissa of greatest value
Skewness for a negatively skewed distribution is less than 0; these distributions have tails that stretch out to values on the abscissa of least value
An example of a positively skewed distribution is that of the typical F density, given in Figure 2.10.
The fourth moment of a distribution is its kurtosis, generally referring to the peakness of a distribution (Upton and Cook, 2002), but also having much to do with a distribution's tails (DeCarlo, 1997):
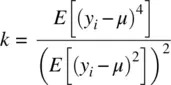
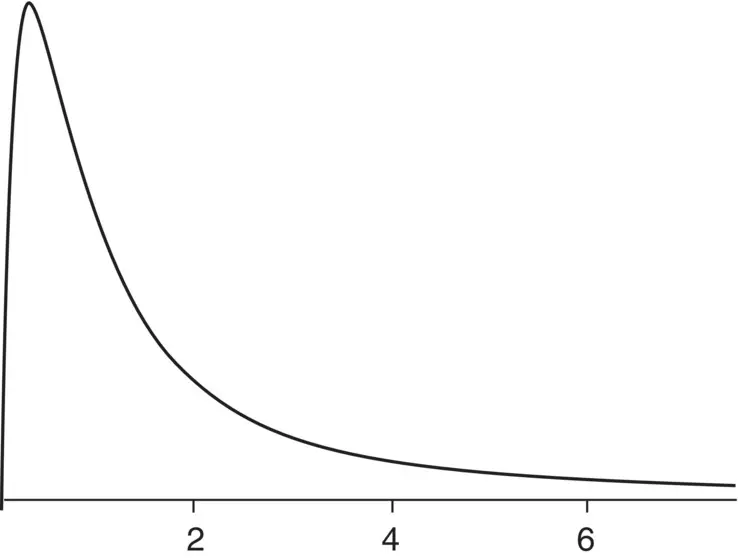
Figure 2.10 F distribution on 2 and 5 degrees of freedom. It is positively skewed since the tail stretches out to numbers of greater value.
With regard to kurtosis, distributions are defined:
mesokurtic if the distribution exhibits kurtosis typical of a bell‐shaped normal curve
platykurtic if the distribution exhibits lighter tails and is flatter toward the center than a normal distribution
leptokurtic if the distribution exhibits heavier tails and is generally more narrow in the center than a normal distribution, revealing that it is somewhat “peaked”
We can easily compute moments of empirical distributions in R or SPSS. Several packages in R are available for this purpose. We could compute skewness for parent on Galton's data by:
> library(psych) > skew(parent) [1] -0.03503614
The psychpackage (Revelle, 2015) also provides a range of descriptive statistics:
> library(psych) > describe(Galton) vars n mean sd median trimmed mad min max range skew kurtosis parent 1 928 68.31 1.79 68.5 68.32 1.48 64.0 73.0 9 -0.04 0.05 child 2 928 68.09 2.52 68.2 68.12 2.97 61.7 73.7 12 -0.09 -0.35 se parent 0.06 child 0.08
The skew for child has a value of −0.09, indicating a slightnegative skew. This is confirmed by visualizing the distribution (and by a relatively close inspection in order to spot the skewness):
> hist(child) 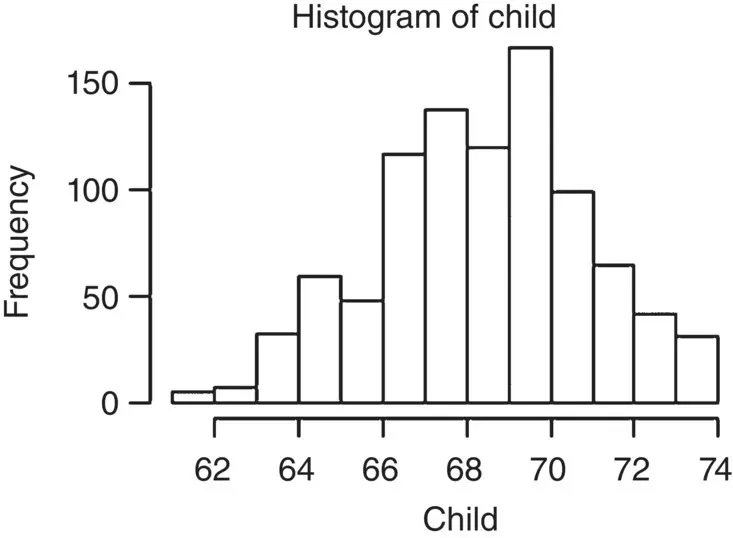
2.11 SAMPLING DISTRIBUTIONS
Sampling distributions are at the cornerstone of statistical inference. The sampling distribution of a statistic is a theoretical probability distribution of that statistic. As defined by Degroot and Schervish (2002), “the sampling distribution of a statistic tells us what values a statistic is likely to assume and how likely it is to assume those values prior to observing our data” (p. 391).
As an example, we will generate a theoretical sampling distribution of the mean for a given population with mean μ and variance, σ 2. The distribution we will create is entirely idealizedin that it does not exist in nature anywhere. It is simply a statistical theoryof how the distribution of means might look if we were able to take an infinite number of samplesof a given size from a given population, and on each of these samples, calculate the sample mean statistic.
When we derive sampling distributions for a statistic, we are asking the following question:
If we were to draw an infinite number of samples of size n from this population and calculate the sample mean on each sample, what would the distribution of sample means look like?
If we can specify this distribution, then we can evaluate obtained sample means relativeto it. That is, we will be able to compare our obtained means (i.e., the ones we obtain in real empirical research) to the theoretical sampling distribution of means, and answer the question:
If my obtained sample mean really did come from this population, what is the probability of obtaining a mean such as this?
If the probability is low, you might then decide to reject the assumption that the sample mean you obtained arose from the population in question. It could have, to be sure, but it probablydid not. For continuous measures, our interpretation above is slightly informal, since the probability of any particular valueof the sample mean in a continuous distribution is essentially equal to 0 (i.e., in the limit, the probability equals 0). Hence, the question is usually posed such that we seek to know the probability of obtaining a mean such as the one we obtained or more extreme.
2.11.1 Sampling Distribution of the Mean
Since we regularly calculate and analyze sample means in our data, we are often interested in the sampling distribution of the mean. If we regularly computed medians, we would be equally as interested in the sampling distribution of the median.
Recall that when we consider any distribution, whether theoretical or empirical, we are usually especially interested in knowing two things about that distribution: a measure of central tendencyand a measure of dispersionor variability. Why do we want to know such things? We want to know these two things because they help summarize our observations, so that instead of looking at each individual data point to get an adequate description of the objects under study, we can simply request the mean and standard deviation as telling the story (albeit an incomplete one) of the obtained observations. Similarly, when we derive a sampling distribution, we are interested in the mean and standard deviation of that theoretical distribution of a statistic.
We already know how to calculate means and standard deviations for real empirical distributions. However, we do not know how to calculate means and standard deviations for sampling distributions. It seems reasonable that the mean and standard deviation of a sampling distribution should depend in some way on the given population from which we are sampling. For instance, if we are sampling from a population that has a mean μ = 20.0 and population standard deviation σ = 5, it seems plausible that the sampling distribution of the mean should look different than if we were sampling from a population with μ = 10.0 and σ = 2. It makes sense that different populations should give rise to different theoretical sampling distributions.
What we need then is a way to specify the sampling distribution of the mean for a given population. That is, if we draw sample means from this population, what does the sampling distribution of the mean look like for this population? To answer this question, we need both the expectation of the sampling distribution (i.e., its mean) as well as the standard deviation of the sampling distribution (i.e., its standard error (SE)). We know that the expectation of the sample mean 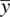 is equal to the population mean μ . That is,
is equal to the population mean μ . That is, 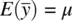 . For example, for a sample mean
. For example, for a sample mean 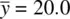 , the expected value of the sample mean is equal to the population mean μ of 20.0.
, the expected value of the sample mean is equal to the population mean μ of 20.0.
Читать дальше

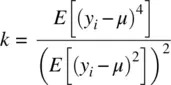


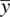 is equal to the population mean μ . That is,
is equal to the population mean μ . That is, 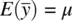 . For example, for a sample mean
. For example, for a sample mean 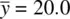 , the expected value of the sample mean is equal to the population mean μ of 20.0.
, the expected value of the sample mean is equal to the population mean μ of 20.0.










