Daniel J. Denis - Applied Univariate, Bivariate, and Multivariate Statistics

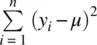The key point is that when we are working with expectations, we are working with probabilities. Thus, instead of summing squared deviations of the kind as one does in the sample or population variance for which there is specified n , one must rather assign to these squared deviations probabilities, which is what is essentially being communicated by the notation “ E ( y i− μ ) 2.” We can “unpack” this expression to read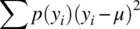

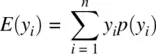
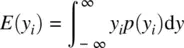
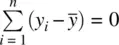where p ( y i) is the probability of the given deviation, ( y i− μ ), for in this case, a discrete random variable.

When we speak of momentsof a distribution or of a random variable, we are referring to such things as the mean, variance, skewness, and kurtosis.

The first moment of a distribution is its mean. For a discrete random variable y i, the expectation is given by:

where y iis the given value of the variable, and p ( y i) is its associated probability. When y iis a continuous random variable, the expectation is given by:

Notice again that in both cases, whether the variable is discrete or continuous, we are simply summing productsof values of the variable with its probability, or densityif the variable is continuous. In the case of the discrete variable, the products are “explicit” in that our notation tells us to take each value of y (i.e., y i) and multiply by the probability of that given value, p ( y i). In the case of a continuous variable, the products are a bit more implicitone might say, since the “probability” of any particularvalue in a continuous density is equal to 0. Hence, the product y i p ( y i) is equal to the given value of y imultiplied by its corresponding density.

The arithmetic mean is a point such that . That is, the sum of deviations around the mean is always equal to 0 for any data set we may consider. In this sense, we say that the arithmetic mean is the center of gravityof a distribution, it is the point that “balances” the distribution (see Figure 2.8).

We often wish to analyze data simultaneously on several response variables. For this, we require vector and matrix notation to express our responses. The matrix operations presented here are surveyed more comprehensively in the Appendix and in any book on elementary matrix algebra.

Figure 2.8Because the sum of deviations about the arithmetic mean is always zero, it can be conceptualized as a balance point on a scale.

Consider the following vector:

where y 1is observation 1 up to observation y n.

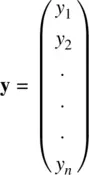
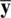We can write the sample mean vector for several variables y 1through y pas

where is the mean of the p thvariable.

The expectation of individual observations within each vector is equal to the population mean μ , of which the expectation of the sample vector yis equal to the population vector, μ. This is simply an extension of scalar algebra to that of matrices:

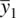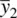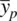Likewise, the expectations of individual sample means , , … are equal to their population counterparts, μ 1, μ 2, … μ p. The expectation of the sample mean vector 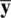is equal to the population mean vector, μ: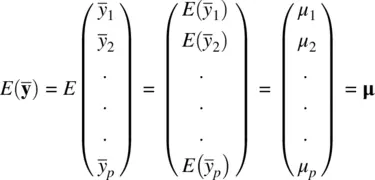

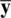We note also that is an unbiasedestimator of μsince .

Recall that we said that the mean is the first moment of a distribution. We discuss the second moment of a distribution, that of the variance, shortly. Before we do so, a brief discussion of estimation is required.

The goal of statistical inference is, in general, to estimate parameters of a population. We distinguish between point estimators and interval estimators. A point estimatoris a function of a sample and is used to estimate a parameter in the population. Because estimates generated by estimators will vary from sample to sample, and thus have a probability distribution associated with them, estimators are also often random variables. 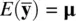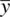For example, the sample mean is an estimator of the population mean μ . However, if we sample a bunch of 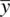from a population for which μ is the actual population mean, we know, both from experience and statistical theory, that 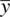will vary from sample to sample. This is why the estimator 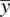is often a random variable, because its values will each have associated with them a given probability (density) of occurrence. When we use the estimator to obtain a particular number, that number is known as an estimate. An interval estimatorprovides a range of values within which the true parameter is hypothesized to exist within some probability. A popular interval estimator is that of the confidence interval, a topic we discuss later in this chapter.